7.4. Определение точечной и интервальной оценок результата измерений

При обработке результатов неравноточных измерений возникают 2 случая: когда известны СКО результатов измерений для каждой серии и когда неизвестны СКО, но известны объемы выборок для каждой серии .

Серии наблюдений при неравноточных измерениях вносят различный вклад в общую оценку результата измерений. Величина вклада серии в итоговую оценку определяется весом серии.

Если известны СКО серий ( , где количество серий), то вес j-ой серии определяется по формуле

,

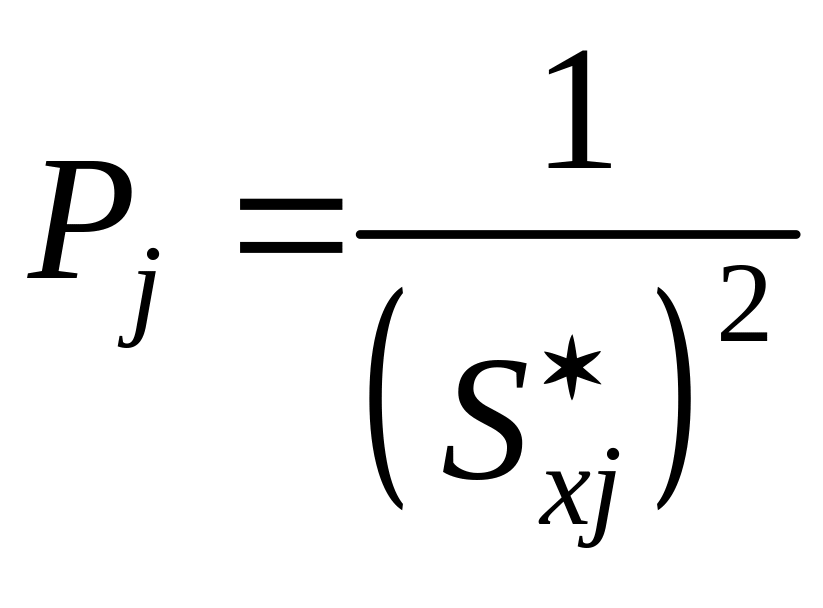где – СКО результата измерения для j-ой серии.

Если СКО серий неизвестны, но известны объемы выборок, то вес j-ой серии можно определить как

,

где – объем выборки j-ой серии.

За оценку результата неравноточных измерений принимается средневзвешенное значение, которое определяется по формуле

,

где – количество серий наблюдений,

– вес j-ой серии,

– координата центра распределения j-ой серии.

Оценка СКО серий наблюдений определяется по формуле

,

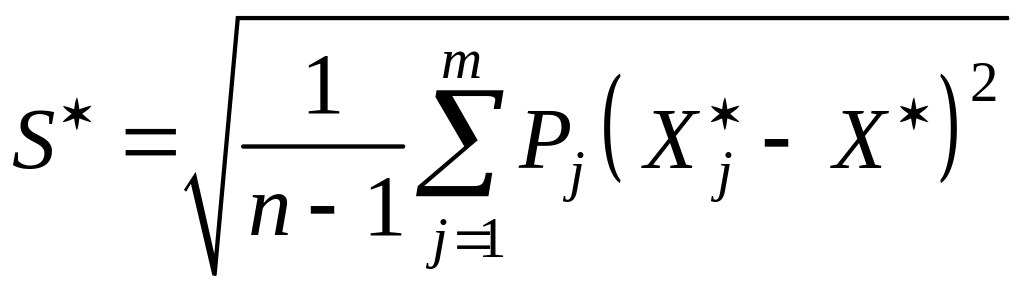где .

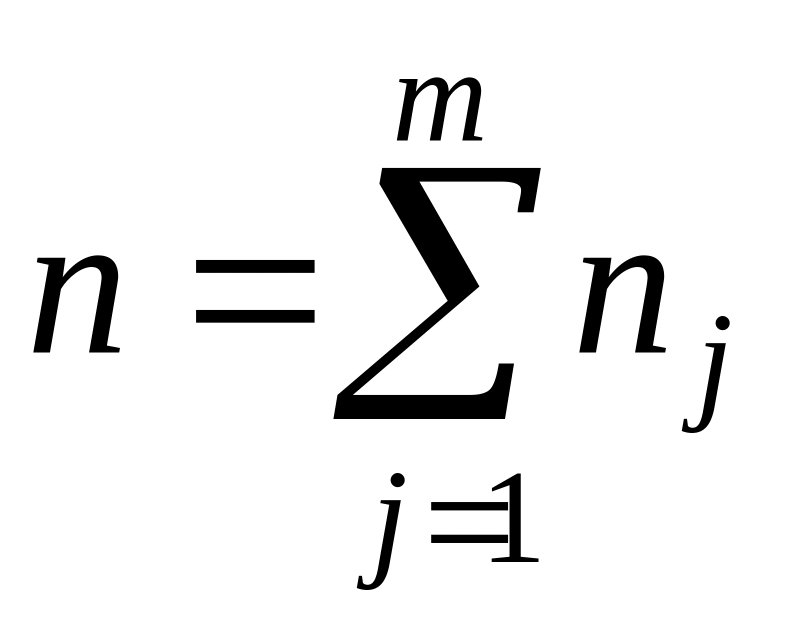Оценка СКО результата неравноточных измерений (СКО средневзвешенного значения)

.

Доверительная граница случайной погрешности результата неравноточных измерений в случае симметричного доверительного интервала находится по формуле

,

где – квантиль распределения Стьюдента с числом степеней свободы , при заданной доверительной вероятности (определяется по формулам или ).

Доверительная граница систематической погрешности определяется по формуле

,

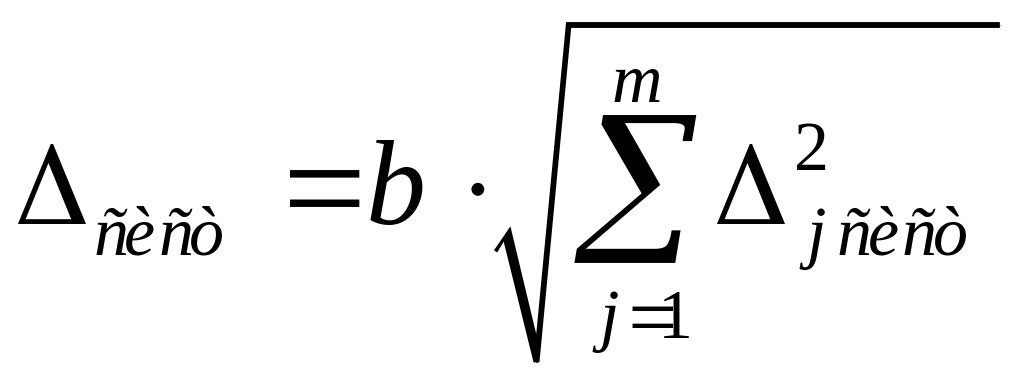где – граница неисключенной систематической погрешности для j-ой серии, которая определяется методами, описанными в п.4.8.3.,

– коэффициент зависимости отдельных неисключенных систематических погрешностей от выбранной доверительной вероятности

p	b
0.90 0.95 0.99	0.95 1.11 1.40

Суммирование систематической и случайной погрешности производится методами, описанными в п.4.8.1.

Пример Для выборок из предыдущего примера вычислить результат неравноточных измерений и его интервальную оценку (без учета систематических погрешностей) при доверительной вероятности р = 0.95 xi1 xi2 xi3 xi4 3 4 8 14 17 2 5 8 11 15 9 11 15 20 22 4 6 8 10 16 Решение: Из предыдущих примеров имеем - выборочные средние арифметические , , , - несмещенные оценки дисперсий , , , . Кроме того, было установлено, что выборки имеют статистически неразличимые дисперсии и равные центры распределений, следовательно они однородны и являются неравноточными сериями наблюдений одной и той же физической величины с вероятностью . Вычислим квадраты СКО результатов измерений для каждой серии по формуле . Вычислим веса для каждой серии по формуле Вычислим сумму весов . Вычислим результат измерения по формуле . Определим общий объем наблюдений . Вычислим оценку стандартного отклонения результатов наблюдений по формуле . Вычислим стандартное отклонение результата измерения по формуле . Вычислим доверительную границу случайной погрешности результата измерения при доверительной вероятности по формуле Число степеней свободы . Квантиль распределения Стьюдента вычислим с помощью аппроксимации Морана . Квантиль стандартного нормального распределения определим по формуле , тогда и граница случайной погрешности . 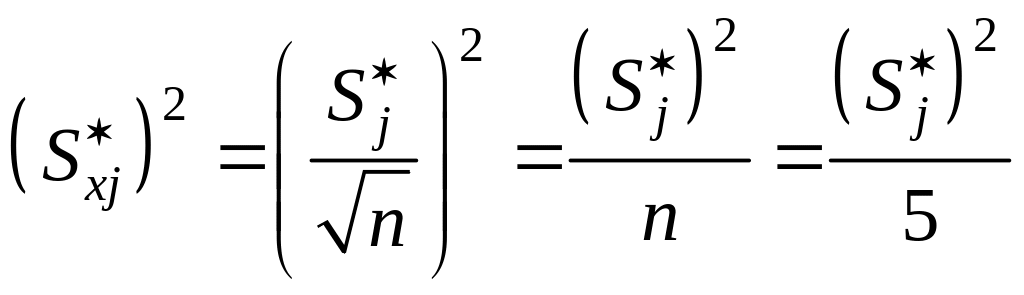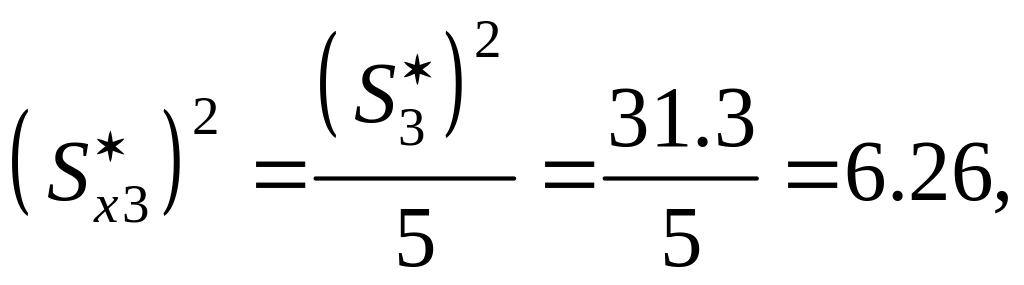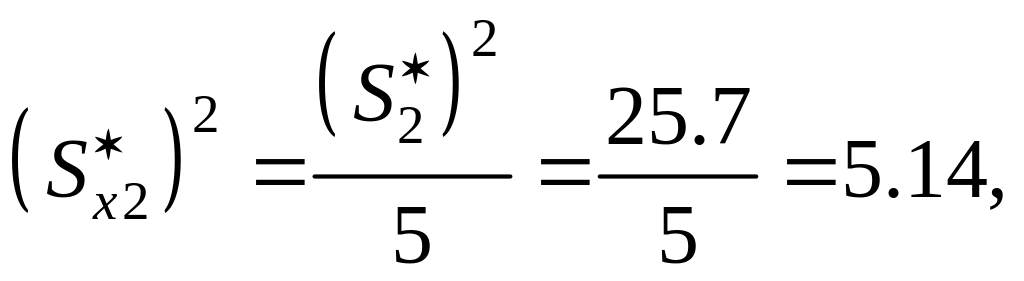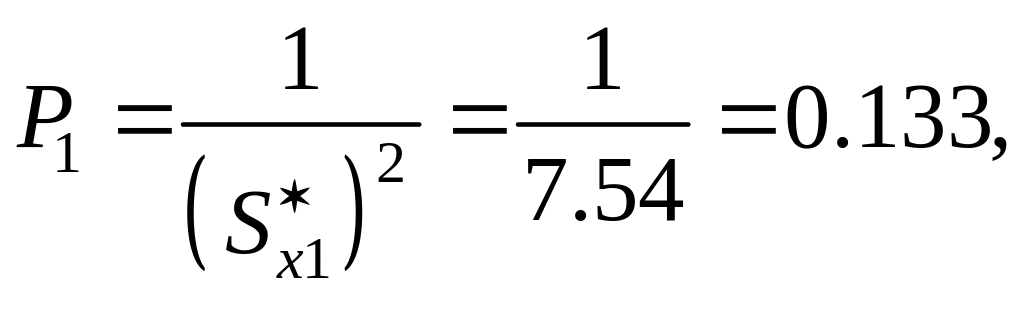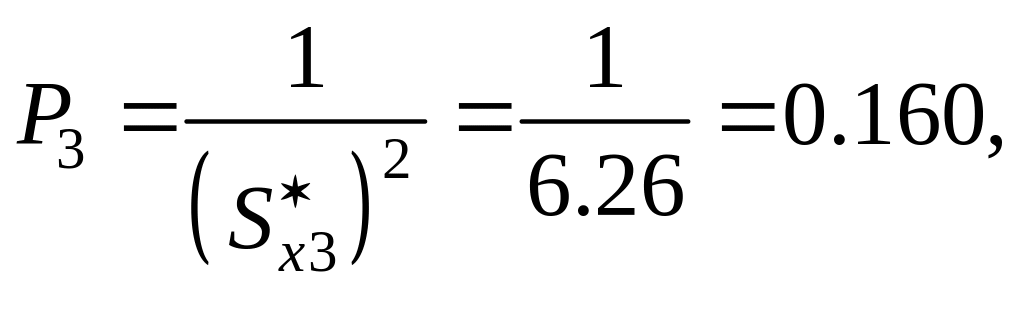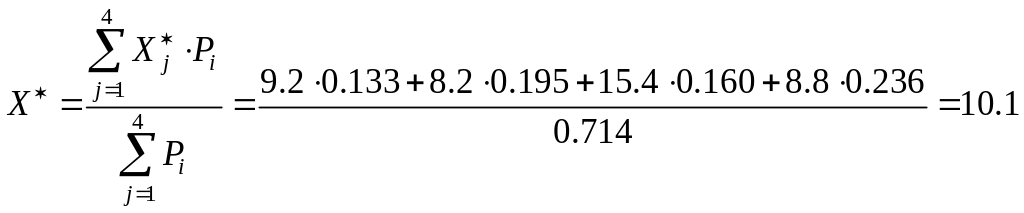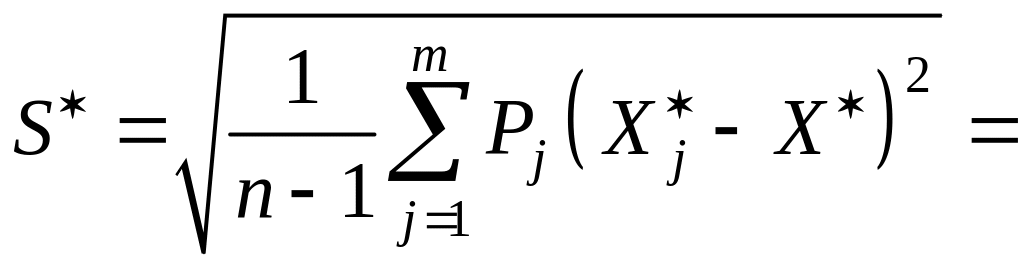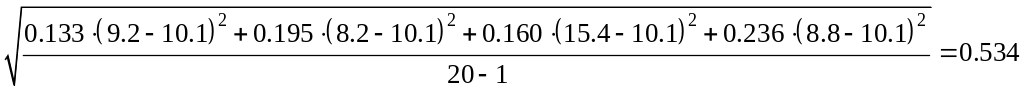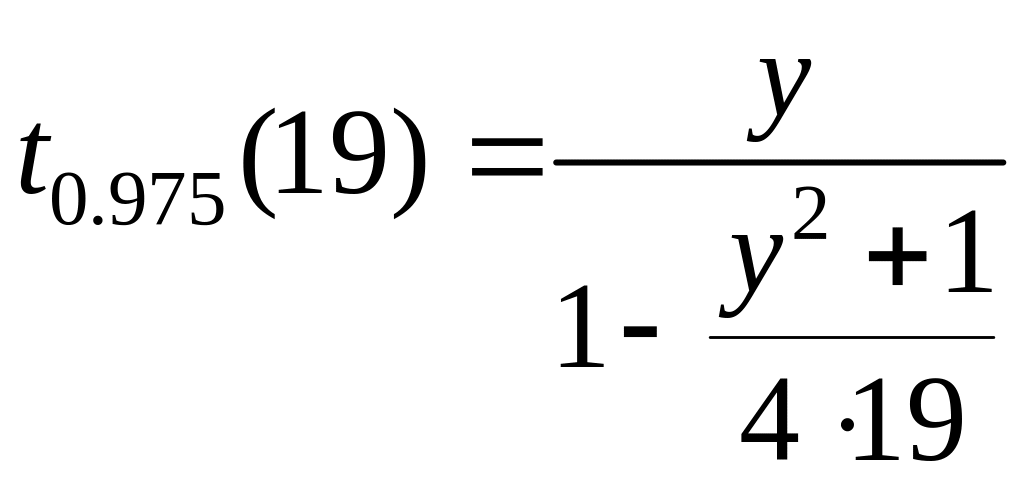Округлим до точности (1 знак после запятой) , получим , тогда доверительный интервал результата измерения , т.е. .