
- •Аннотация
- •1. Основы теории измерений
- •1.1. Понятия “эксперимент” и “экспериментальные данные”. Источники и пути повышения точности экспериментальных данных
- •1.2. Основные понятия и определения теории измерений
- •1.3. Классификация погрешностей результатов измерений
- •2. Основы теории вероятностей и математической статистики
- •2.1. Случайная величина. Интегральная и дифференциальная функции распределения случайной величины и их свойства.
- •2.2. Генеральная и статистическая (выборочная) совокупности. Статистический ряд и способы его представления
- •2.3. Статистические (эмпирические) функции распределения
- •2.4. Статистические оценки параметров распределения случайной величины и их свойства
- •2.5. Статистические гипотезы
- •3. Основные законы распределения
- •3.1. Распределение Гаусса (нормальное распределение)
- •3.2. Распределение Пирсона
- •3.3. Распределение Стьюдента
- •3.4. Распределение Фишера
- •3.5. Экспоненциальное и логнормальное распределения
- •3.6. Равномерное и треугольное распределения
- •4. Обработка результатов прямых многократных измерений
- •4.1. Понятие о прямых многократных измерениях. Общий алгоритм обработки результатов наблюдений
- •4.2. Оценки центра распределения результатов наблюдений, оценка результата измерения
- •4.3. Моменты случайной величины и их оценки, оценки стандартных отклонений результатов наблюдений и результата измерения
- •4.4. Коэффициенты формы закона распределения случайной величины и их оценки
- •4.5. Устранение грубых ошибок прямых многократных измерений
- •4.5.1. Исключение промахов проверкой статистических гипотез
- •4.5.2. Исключение промахов универсальным методом
- •4.6. Исключение переменной составляющей систематической погрешности
- •4.7. Определение вида закона распределения результатов наблюдений
- •4.7.1. Определение вида закона распределения методом моментов
- •4.7.2. Критерии принадлежности результатов наблюдений к нормальному закону распределения
- •4.8. Интервальная оценка результата измерения
- •4.8.1. Определение доверительного интервала результата измерения
- •4.8.2. Определение границ случайной погрешности
- •4.8.3. Определение границ неисключенной систематической погрешности
- •5. Правила округления результатов измерений
- •6. Обработка результатов прямых однократных измерений
- •7. Обработка результатов неравноточных измерений
- •7.1. Понятие о неравноточных измерениях. Общий алгоритм обработки результатов неравноточных измерений
- •7.2. Проверка гипотезы о равенстве дисперсий
- •7.3. Проверка гипотезы о равенстве центров распределений
- •7.4. Определение точечной и интервальной оценок результата измерений
- •8. Обработка результатов косвенных измерений
- •8.1. Косвенные измерения. Коэффициент корреляции
- •8.2. Критерии значимости корреляционной связи
- •8.3. Определение стандартного отклонения результата измерения
- •8.4. Определение доверительного интервала результата измерения
- •9. Основы теории интерполяции
- •9.1. Основные понятия и определения теории интерполяции
- •9.2. Интерполяция точная в узлах
- •9.2.1. Конечные и разделенные разности
- •9.2.2. Интерполяция кусочно-линейными функциями
- •9.2.3. Интерполяция полиномами
- •9.3. Аппроксимация
- •9.3.1. Наиболее часто используемые функции
- •9.3.2. Методы выбора аппроксимирующей функции
- •9.3.3. Методы аппроксимации
- •10. Обработка результатов совместных измерений
- •10.1. Понятие о совместных измерениях и регрессии. Задачи статистического исследования регрессии
- •Статистический анализ коэффициентов регрессии.
- •10.2. Регрессия элементарными функциями
- •10.3. Регрессия полиномами
- •10.4. Статистический анализ коэффициентов регрессии
- •10.5. Устранение грубых ошибок измерения
- •10.6. Построение доверительной области регрессии.
- •10.7. Проверка соответствия уравнения регрессии экспериментальным данным
- •Вопросы к экзамену
- •Правила округления результатов измерений.
- •Понятие о неравноточных измерениях. Общий алгоритм обработки результатов неравноточных измерений.
- •Критерии значимости корреляционной связи.
- •Понятие о совместных измерениях и регрессии. Задачи статистического исследования регрессии.
- •Регрессия элементарными функциями.
- •Основные понятия и определения теории интерполяции.
- •Конечные и разделенные разности.
- •Интерполяция кусочно-линейными функциями.
- •Список рекомендуемой литературы
3.4. Распределение Фишера
Если две независимые
случайные величины
![]() и
и
![]() распределены по закону Пирсона со
степенями свободы, соответственно,
распределены по закону Пирсона со
степенями свободы, соответственно,
![]() и
и
![]() ,
то случайная величина
,
то случайная величина
 имеет распределение Фишера (F-распределение)
со степенями свободы
и
.
имеет распределение Фишера (F-распределение)
со степенями свободы
и
.
Обозначение |
|
Параметры |
|
Плотность вероятности |
|
Функция распределения |
|
Среднее |
|
Дисперсия |
|
F-распределение широко применяется при обработке данных (при сравнении дисперсий, анализе корреляций).
Квантиль распределения Фишера при известных значениях степеней свободы и и при заданном значении доверительной вероятности p можно найти, например, с помощью аппроксимации Воглера-Нортона
 ,
,
где
 ,
, ,
,
![]() – p-квантиль
стандартного нормального распределения,
значение которого вычисляется по
формулам и .
– p-квантиль
стандартного нормального распределения,
значение которого вычисляется по
формулам и .
Пример
Вычислить с
помощью аппроксимации Воглера-Нортона
значения
Решение:
По условию задачи
Вычислим коэффициенты
Найдем квантиль
стандартного нормального распределения
при
тогда
и по формуле
Найдем квантиль
стандартного нормального распределения
при
тогда
и
|
3.5. Экспоненциальное и логнормальное распределения
Экспоненциальное распределение – это одно из наиболее часто встречающихся распределений в теории надежности. Используется для описания внезапных отказов, когда износом изделия можно пренебречь. Наработка на отказ многих невосстанавливаемых изделий и наработка между соседними отказами у восстанавливаемых изделий в случае простейшего потока отказов подчинены экспоненциальному распределению. Наработка на отказ большой многокомпонентной системы может быть описана экспоненциальным распределением при любом распределении наработки на отказ компонентов системы.
Обозначение |
|
Параметр |
|
Плотность вероятности |
|
Функция распределения |
|
Среднее |
|
Дисперсия |
|
Стандартное отклонение |
|
Коэффициент вариации |
1 |
Коэффициент асимметрии |
2 |
Коэффициент эксцесса |
6 |
Медиана |
|
Пример
Наработка на
отказ прибора распределена экспоненциально
с интенсивностью отказов
Решение: Вероятность того, что наработка на отказ превысит 1000 ч, равна
Вероятность того, что наработка будет находиться в интервале от 1200 ч до 1500 ч, определяем по свойству функции распределения
Наработку
то есть
При снижении интенсивности отказов до
|
Двойное
экспоненциальное распределение (в
записи функций вместо
используется
![]() )
называется распределением Лапласа.
)
называется распределением Лапласа.
Если случайная
величина Y
распределена нормально, то случайная
величина
![]() подчинена логарифмически
нормальному
(или логнормальному)
закону распределения. Часто используется
для описания износовых отказов. У многих
невосстанавливаемых электронных
приборов (некоторые типы электронных
ламп, полупроводниковые приборы)
наработка на отказ распределена
логарифмически нормально.
подчинена логарифмически
нормальному
(или логнормальному)
закону распределения. Часто используется
для описания износовых отказов. У многих
невосстанавливаемых электронных
приборов (некоторые типы электронных
ламп, полупроводниковые приборы)
наработка на отказ распределена
логарифмически нормально.
Обозначение |
|
Параметры |
|
Плотность вероятности |
|
Функция распределения |
|
Среднее |
|
Дисперсия |
|
Коэффициент вариации |
|
Коэффициент асимметрии |
|
Коэффициент эксцесса |
|
Медиана |
|
Распределение имеет положительную асимметрию. Произведение независимых случайных величин, подчиняющихся логарифмически нормальному распределению, также распределено логарифмически нормально.
При вычислениях, связанных с логарифмически нормальным распределением, пользуются приемами для нормального распределения, заменяя при этом значение случайной величины ее логарифмом.
Логарифмически нормальное распределение иногда ошибочно принимается за экспоненциальное. Распределение случайной величины близко к логнормальному, если
 ,
,
где
– объем выборки,
 ,
,
 ,
,
![]() – результаты
наблюдений.
– результаты
наблюдений.



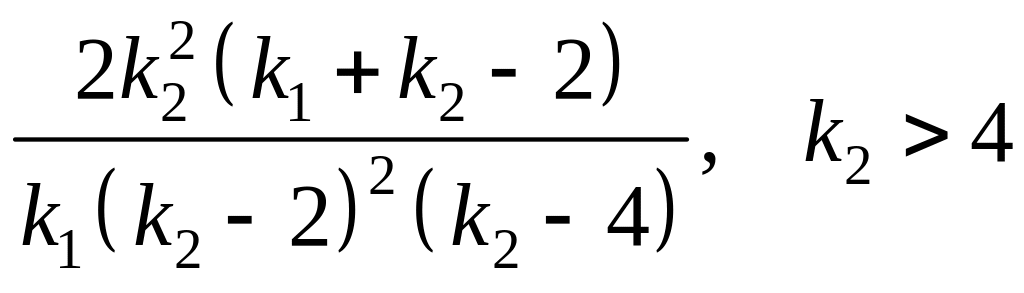
 .
. .
.

