5575

ББК З Х12

Нечёткая логика : лабораторный практикум для бакалавров IV курса направления 230700.62 «Прикладная информатика в экономике» очной формы обучения / сост. Л. Я. Матюхина, С. Е. Злаина. – Хабаровск : ХГАЭП, 2013. – 56 с.

Рецензенты: к.ф-м.н., доцент кафедры «высшей математики» ДВГУПС Ушакова Г. А.

к.ф-м.н., доцент, завкафедрой САПР ДВГУПС, доктор PHD Пономарчук Ю.В.

Утверждено издательско-библиотечным советом академии в качестве лабораторного практикума для студентов

© Хабаровская государственная академия экономики и права, 2013

Содержание

Введение……………………………………………………..……….………….…4

1.Основные понятия и определёния нечёткой логики..………………….…….5

2.Лабораторный практикум

2.1.Лабораторная работа 1. Метод максиминной свёртки……………...…13

2.2.Лабораторная работа 2. Моделирование нечётких систем …….…..…17

2.3.Лабораторная работа 3. Метод аддитивной свёртки………..……...….37

2.4.Лабораторная работа 4. Метод лингвистических векторных оценок ..42

2.5.Лабораторная работа 5. Нечёткая нейронная сеть типа ANFIS…...…45 Библиографический список…………………………………………………..….55

4

Введение

Лабораторный практикум состоит из пяти лабораторных работ по нечёткой логике. Для выполнения этих работ используется программный пакет

MATLAB 6.5.

Влабораторной работе 1 рассматриваются основы нечёткой логики и конкретный пример применения лингвистических векторных оценок.

Влабораторной работе 2 рассматривается метод аддитивной свёртки.

Влабораторной работе 3 рассматривается теория нейронных сетей и её реализация в программе MATLAB 6.5. Изучается структура однослойных и многослойных нейронных сетей, реализовывается процесс обучения нейронной сети, а также применения сетей для решения экономических задач.

Влабораторной работе 4 рассматривается построение гибридной системы с использованием программы MATLAB 6.5.

Во всех лабораторных работах формулируются индивидуальные задания для студентов и задаются контрольные вопросы.

Все лабораторные работы должны быть оформлены согласно стандарту академии и защищены до начала сессии.

Вбиблиографическом разделе приведён список источников основной и дополнительной литературы.

5

Основные понятия и определёния

Принять решение – значит смириться с перевесом одних внешних факторов над другими. Александр Твардовский С помощью слов можно двигать горы!

Уинстон Черчель

В узком смысле нечёткая логика – это логическое исчисление, являющееся расширением многозначной логики. В широком смысле – нечёткая логика равнозначна теории нечётких множеств. Элементы теории нечётких множеств могут успешно применяться для решения задач в условиях неопределённости. Основатель теории нечётких множеств Л. Заде ещё в 1965 году написал «Фактически нечёткость может быть ключом к пониманию способности человека справляться с задачами, которые слишком сложны для решения на ЭВМ».

Нечётким множеством A во множестве U называется совокупность пар вида (u, A (u)), где u U , а A (u) – это функция принадлежности нечёткого множества A, A :U [0,1].

Нечёткое множество A называется пустым, если A (u) 0, u U. Носителем нечёткого множества А называется обычное подмножество

таких точек U, для которых величина A (u) положительна. Высотой нечёткого множества А называется величина supU A (u).

Точкой перехода нечёткого множества А называется такой элемент множества 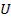, степень принадлежности которого множеству А равна 0,5.

6

3. Объединение. Объединением ( A B ) нечётких множеств A и B называют наименьшее нечёткое подмножество A B , с функцией принадлежности вида:

A B (u) min( A (u),1 A (u)) .

7.Дизъюнктивная сумма ( A B) . Дизъюнктивная сумма нечётких множеств

maxu A A (u) 1, то нечёткое множество A имеет функцию принадлежности:

7

5. Выпуклая комбинация. Выпуклой комбинацией нечётких множеств A1 A2 ... An в U называется нечёткое множество A с функцией принадлежности вида:

Выпуклые комбинации нечётких множеств нужны для принятия решений с несколькими нечёткими ограничениями. Для обычных множеств эта операция

подмножества универсальных множеств U1,U2 ,...,Un соответственно. Декартово

Нечёткое число – это нечёткое подмножество универсального множества действительных чисел, имеющих нормальную и выпуклую функции принадлежности.

Нечёткие числа (L – R)-типа – это разновидность нечётких чисел специального вида, то есть задаваемых по определённым правилам с целью

- r u(r) u(r) .

Данное определёние позволяет ввести понятие меры и превратить множество нечётких чисел в топологическое пространство.

Нечёткие числа соответствуют значениям числовой лингвистической

определяется следующим образом:

8

x a , если x [a, b],b a

A(x) x c , если x [b, c],b c

0, в ином случае.

Второе число b тройки a,b,c обычно называют модой или чётким значением нечёткого треугольного числа. Числа a и c характеризуют степень размытости чёткого числа.

При ограничении нечётких чисел до понятия треугольных чисел не позволяет решить проблемы противоположного, обратного элементов и дистрибутивности.

Например, при умножении двух нечётких чисел получается более размытое нечёткое число, и чем больше операнды, то есть, чем дальше от нуля они находятся на числовой оси, тем более размытым получается результат.

X – наименование нечёткой переменной.

U {u} область её определёния (универсальное множество).

ограничения на значения некоторой переменной X .

Значениями лингвистической переменной являются слова или предложения в естественном или формальном языке. Понятие лингвистической переменной позволяет приближенно описывать явления, не поддающиеся описанию в общепринятых количественных терминах.

Совокупность значений лингвистической переменной составляет терммножество этой переменной. Это множество может иметь бесконечное число элементов.

Важным аспектом понятия лингвистической переменной является то, что это переменная более высокого порядка, чем нечёткая переменная, в том смысле, что значениями лингвистической переменной являются нечёткие переменные.

9

Другой важный аспект понятия лингвистической переменной состоит в том, что лингвистической переменной соответствуют два правила:

-синтаксическое правило – может быть задано в форме грамматики, порождающей названия значений переменной;

-семантическое правило – определяет алгоритмическую процедуру для вычисления смысла каждого значения.

Лингвистическая переменная характеризуется набором ( X ,T ( X ),U , G, M ) в котором:

X – название переменной;

T ( X ) – (или просто T ) обозначает терм-множество переменной X , то есть множество названий лингвистической переменной X , причём каждое из таких значений является нечёткой переменной Х со значениями из универсального

множества его смысл, можно задать алгоритмически. Тогда, синтаксические и семантические правила, связанные со структурированной лингвистической переменной, можно рассматривать как алгоритмические процедуры для порождения элементов множества T ( X ) и вычисления смысла каждого терма в

UR1 , R1 ( ,) , и которая имеет измеримую базовую переменную.

Вобщем случае нечётким отношением, заданным на множествах (универсумах) X1 , X 2 ,..., X k , называется некоторое фиксированное нечёткое

подмножество декартова произведения этих универсумов. Другими словами, если обозначить произвольное нечёткое отношение через Q, то по определёнию

10

Q={<х1, х2,…,xk >, μQ< х1, х2,…,xk >} , где μQ< х1, х2,…,xk > функция при-

надлежности данного нечёткого отношения, которая определяется как отображение Q : X1 X 2 ... X k 0,1 . Здесь через < х1, х2,…,xk > обозначен кортеж из k элементов, каждый из которых выбирается из своего универсума: x1 X1 , x2 X 2 ,...,xk X k .

Пустое нечёткое отношение определяется как отношение, которое не содержит ни одного кортежа A (u) 0, u U , где U – некоторое обычное множество, называемое универсальным.

Способы задания нечётких отношений:

-в форме списка с явным перечислением всех кортежей нечёткого отношения и соответствующих им значений функции принадлежности;

-аналитически в форме некоторого математического выражения для соответствующей функции принадлежности этого нечёткого отношения;

-графически в форме некоторой поверхности или совокупности отдельных точек в трёхмерном пространстве;

-в форме матрицы нечёткого отношения;

-в форме нечёткого графа, который формально может быть задан в виде двух обычных конечных множеств и некоторой функции принадлежности.

В зависимости от количества кортежей нечёткое отношение может быть конечным или бесконечным. Нечёткое отношение называется конечным, если его носитель является конечным отношением. При этом вполне уместно говорить, что такое нечёткое отношение имеет конечную мощность, которая численно равна количеству кортежей его носителя, рассматриваемого как обычное множество. В этом случае для обозначения мощности произвольного нечёткого отношения Q можно использовать общепринятое обозначение card(Q). Аналогично счётным нечётким отношением будем называть нечёткое отношение со счётным носителем, т. е. носитель которого имеет счётную мощность в обычном смысле. Несчётным нечётким отношением называется нечёткое отношение с несчётным носителем, т. е. носитель которого имеет несчётную мощность или мощность континуума С (или N) в обычном смысле.