5531

Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Хабаровский государственный университет экономики и права

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Берём на главной диагонали элементы aii

и a jj , где номера i и j получены на

1-м шаге. Находим угол поворота

Составим матрицу поворота H , в которой:

.pdf

Скачиваний:

Добавлен:

13.11.2022

Размер:

1.75 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 56 / 86 7 8 > Следующая >>>

	X 4	1	0,6	0,2	1,89	3,223
4)	X 4	0,6	1	0,5	2,71	4,577	,
		0,2	0,5	1	1,465	2,442
	X 5	1	0,6	0,2	3,223	5,481
5)	X 5	0,6	1	0,5	4,577	7,731	,
		0,2	0,5	1	2,442	4,086

4,577	1,6887	;

2,71
2,71

	7,731	1,689 3 .

	4,577
	4,577

Замечаем, что и			4 , и	5	с точностью 0,01 равны 1,69. Значит, 1,69 – одно
из собственных чисел. Найдём другие соотношения:										5,481			1,70	и	4,086	1,673.
из собственных чисел. Найдём другие соотношения:													1,70	и		1,673.
										3,223				2,442
Проведём для надёжности дополнительную итерацию:
6) X 6	1		0,6	0,2		5,481		9,302			13,062
	0,6		1 0,5			7,731		13,062	,		13,062			1,6895.
	0,6		1 0,5			7,731		13,062	,	6		7,731		1,6895.
	0,2		0,5	1		4,086		6,855				7,731
	0,2		0,5	1		4,086		6,855
Итак, считаем, что			1,69 – собственное число. Нормируем вектор:

9,3022	13,0622		6,8552		17,44 – длина полученного вектора;
9,302	0,533,	13,062		0,749		,	6,855	0,393 – координаты соответствующего
	0,533,			0,749		,	6,855	0,393 – координаты соответствующего
17,44	17,44					17,44
единичного вектора.
Проверим:
			1		0,6	0,2		0,533	0,904
			0,6		1	0,5		0,749	1,265 .
			0,2		0,5	1		0,393	0,661

Отношения координат в среднем равны собственному числу:

0,904	1,70,	1,265	1,69,	0,661	1,68.

0,533		0,749		0,393

После нормировки собственный вектор совпадёт с предыдущим до сотых. Ответ: одно из собственных чисел с точностью 0,01 равно 1,69, со-

ответствующий собственный вектор X 0,53; 0,75; 0,39 .

Итерационный процесс не будет сходиться, если матрица не имеет собственных чисел. Точнее, если матрица не имеет действительных собственных чисел, то процесс расходится для любого начального действительного приближения.

Пример 3. Требуется найти собственные векторы матрицы	1	2 .
	5	3
51

Решение. Возьмём начальное приближение 11 . Умножая матрицу

на очередное приближение, после деления на первую координату (чтобы иметь возможность сравнить векторы) получим последовательно приближения

1	1	1	1	1	1	1	1	,
1	8	1,118	0,509	359	1,491	0,132	7,341	,
и т.д. Процесс ни к чему не сходится.
Собственные числа этой матрицы 1					2 3i и 2	2	3i – комплекс-

ные. Очевидно, что получить их из каких бы то ни было действительных чисел при помощи операций сложения и умножения (а только такие выполняются при умножении матрицы на столбец) невозможно.

Задача не имеет действительных решений.

Замечание. Для матриц корреляции, когда aii 1 и aij a ji для любых j i , причём aij 1, собственные числа всегда существуют, положительны

иразличны. К сожалению, метод простых итераций даже для таких матриц даёт только одно случайное решение. Чтобы найти все собственные числа

ивекторы матрицы корреляции, нужен более сложный и громоздкий метод вращений.

§7. Метод Якоби приближённого вычисления собственных чисел и собственных векторов 7.1. Основные положения

Пусть дана квадратная матрица

	a11	a1n
An n				.
	an1	ann
Напомним, что нулевой вектор-столбец		X	n 1	x , x	, , x	T	называется	соб-
			n 1	1 2		n
ственным вектором матрицы A , если существует такое число							, что AX	X ,

т.е. если преобразование вектора путем умножения справа на матрицу равносильно обычному умножению на число. Число при этом называется собственным числом матрицы A , соответствующим собственному вектору X .

для 0 , где

Так, вектор X		5	будет собственным для матрицы A								4	1	, по-
	10										6	5
скольку
AX	4	1	5	4	5	1 10	10	2	5	2 X ,
AX	6	5	10	6	5	5 10	20	2	10	2 X ,

т.е. преобразование вектора свелось к умножению на число 2. Это число – собственное.

Задача поиска собственных значений и векторов матриц встречается во многих областях. В экономике это позволяет, например, упростить изучение зависимости некоторой величины от набора факторов, когда эти факторы сами связаны между собой.

Из курса линейной алгебры известно, что поиск собственных чисел матрицы A сводится к решению характеристического уравнения A E

E – единичная матрица, – определитель матрицы А − λЕ.

Однако такое уравнение в общем случае сводится к алгебраическому уравнению степени n относительно неизвестной , решить которое нельзя точно. Кроме того, приближённое решение уравнения позволяет найти только один из n корней. Нужны способы приближённого поиска всех собственных чисел матрицы.

Большинство матриц, возникающих в практических задачах, симметричные, т.е. обладают свойством aij a ji для всех i, j 1, n. Для таких матриц соб-

ственные числа можно найти методом Якоби, иначе называемым методом вращений.

Назовём для краткости верхней частью матрицы А все элементы над её главной диагональю – элементы aij , у которых i j.

7.2. Схема метода Якоби

Итак, дана симметричная матрица A . Необходимо найти собственные числа с точностью , где >0 – необходимая точность решения задачи.

При решении будет составляться матрица собственных векторов, которую обозначим буквой U . Перед началом действий U E , т.е. совпадает с единичной матрицей.

1.Найдём максимальный по модулю элемент в верхней части матрицы A . Пусть это элемент aij . Запомним номер строки i и номер столбца j .

2.Если aij , вычисления закончены. Если нет, переходим к шагу 3.

cos ; a jj

cos ;

а) на главной диагонали элементы aii

б) остальные элементы главной диагонали равны 1;

в) элементы aij	sin	; a ji sin ;
г) все остальные элементы матрицы H равны 0.
5. Находим новую матрицу A		H T AH , где H T – матрица, транспонированная к H .
	new

6. Находим UH и обозначаем буквой U. Матрицу Anew переобозначаем как А.

Переходим к 1-му шагу.

Когда действия закончены, на главной диагонали матрицы A стоят её собственные числа, а каждый столбец матрицы U – это собственный вектор матрицы A . Номер столбца соответствует номеру собственного значения.

Замечание 1. Транспонирование матрицы H , очевидно, сводится к замене знаков у sin , а умножение H T AH по свойствам матриц возможно в любом порядке.

Замечание 2. Векторы, получаемые методом Якоби − нормированные, т.е. единичной длины. В качестве собственного можно взять любой другой вектор, пропорциональный нормированному.

Пример 1. Решим простую задачу 2-го порядка. Найдём с точностью

0,001 собственные числа и векторы матрицы A											7	2 .
											2	4
Решение. Берём U		1		0	. Это заготовка для матрицы собственных век-
		0		1
торов.
Шаг 1. В верхней части матрицы A всего один элемент – число a12 2 .
Он и будет максимальным.
Шаг 2. Поскольку условие						aij		для максимального элемента не выпол-
Шаг 2. Поскольку условие						aij		для максимального элемента не выпол-
нено, действия продолжаются.
Шаг 3. Находим a11		7, a22					4 – элементы напротив максимального. То-
гда угол поворота	0,5arctg		2	2			0,5arctg		4	0,4636.
гда угол поворота	0,5arctg						0,5arctg			0,4636.
		7		4			3
							54

Шаг 4. Находим cos0,4636 0,8944 и sin 0,4636 0,4472. Составляем матрицу поворота

H0,8944 0,4472 .

0,4472 0,8944

Шаг 5. Находим H T		0,8944		0,4472 , тогда
		0,4472		0,8944
Anew	0,8944		0,4472		7	2	0,8944			0,4472
Anew	0,4472		0,8944		2	4	0,4472		0,8944
	0,4472		0,8944		2	4	0,4472		0,8944
Перемножив первую и вторую матрицы, находим далее
A	7,1552		3,5776		0,8944			0,4472		8	0 .
new	1,3416		2,6832		0,4472			0,8944		0	3
	1,3416		2,6832		0,4472			0,8944		0	3
Это новая матрица A .
Шаг 6. Находим U	UH	1	0		0,8944			0,4472			0,8944	0,4472 .
		0	1		0,4472			0,8944			0,4472	0,8944
Это новая матрица U .
Найдено первое приближение решения. Возвращаемся к шагу 1.
Переходим к следующему приближению.
Шаги 1−2. В матрице		A	8	0	единственный элемент верхней части
Шаги 1−2. В матрице		A	0	3	единственный элемент верхней части
			0	3

равен нулю. Поскольку он автоматически максимален, условие окончания вы-

полнено:		0	0,001.
	Ответ: Собственные числа матрицы A				7	2	– числа		8	и		3.
	Ответ: Собственные числа матрицы A				2	4	– числа	1	8	и	2	3.
								1			2

Соответствующие собственные векторы для них						– векторы		U1		0,894		и
Соответствующие собственные векторы для них						– векторы		U1		0,447		и
										0,447
U2	0,447 .
	0,894
	Замечание 3. Можно заметить, что 0,8944 2					0,4472, т.е одна из коорди-
нат вектора			U1	в два раза больше другой. Поэтому можно взять, например,
U1	2 или		U1	100 , и т.п. Из тех же соображений можно взять U2							1	или
	1			50							2

U2 и т.д. Эти векторы уже не нормированные, но также собственные.

Пример 2. Найдём с точностью 0,001 собственные числа и векторы матрицы третьего порядка

2 0,1 0,2

A0,1 10 0,3 .

0,2 0,3 4

Решение. Матрица симметрична, и потому можно применить метод вращений.

Приближение 1

Шаг 1. Максимальный по модулю элемент верхней части – число a23 0,3.

Шаг 2. Условие				0,3		0,001 не выполнено, действия продолжаются..
Шаг 3. Находим a22 10, a33								4 – элементы на главной диагонали напро-
тив максимального. Угол поворота
							0,5arctg			2	0,3	0,04983.
							0,5arctg					0,04983.
									10		4
Шаг 4. Находим cos 0,04983								0,99876 и sin 0,04983						0,04981. Составляем
матрицу поворота
	1		0			0					1	0		0
H	0	0,99876			0,04981 , тогда H T						0	0,99876		0,04981 .
	0	0,04981			0,99876						0	0,04981		0,99876
Шаг 5. Находим A :
Anew H T		1	0			0	2	0,1	0,2		1	0		0
Anew H T	AH	0	0,99876			0,04981	0,1	10	0.3		0	0,99876	0,04981
		0	0,04981			0,99876	0,2	0,3	4		0	0,04981	0,99876
2	0,10984		0,19477
0,10984	10,01496		0 .
0,19477		0	3,98504

Шаг 6. В 1-м приближении матрица U совпадает с 1-й матрицей поворо-

та:

1 0 0

U 0 0,99876 0,04981 . 0 0,04981 0,99876

Найдено 1-е приближение решения. Возвращаемся к шагу 1.

Приближение 2

Шаг 1. Находим максимальный по модулю элемент верхней части a13 0,19477.

Шаг 2. Условие 0,19477 0,001 не выполнено.

	Шаг 3. На главной диагонали a11											2, a33	3,98504. Угол поворота
		0,5arctg			2	0,19477				0,09689.
		0,5arctg								0,09689.
				2		3,98504
	Шаг 4.		Поскольку					cos		0,09689 0,99531 и				sin		0,09689		0,09674, то
матрица поворота имеет вид
		0,99531				0	0,09674					0,99531		0	0,09674
	H		0			1		0		, тогда H T			0	1		0	.
		0,09674				0	0,99531					0,09674		0	0,99531
	Шаг 5. Находим A :
	0,99531		0	0,09674				2		0,10984		0,19477	0,99531		0	0,09674
Anew		0	1	0			0,10984			10,01496		0	0		1		0
	0,09674		0	0,99531			0,19477				0	3,98504	0,09674		0	0,99531
	1,98107	0,10932		0
	0,10932	10,01496		0,01063 .
	0	0,01063		4,00397
	Шаг 6. Умножим предыдущую матрицу U на новую матрицу поворота:
	1	0		0				0,99531			0	0,09674	0,99531				0	0,09674
U	0	0,99876		0,04981				0			1	0	0,00482				0,99876	0,04958 .
	0	0,04981		0,99876				0,09674			0	0,99531	0,09662				0,04981	0,99407
	Приближение 3
	Шаг 1. Максимальный по модулю элемент верхней части a12																	0,10932.

	Шаг 2. Условие						0,10932			0,001 не выполнено.
	Шаг 3. Находим a11								1,98107, a22			10,01496. Угол поворота

	0,5arctg		2	0,10932			0,0136.

		1,98107 10,01496
Шаг 4. Находим cos					0,0136		0,99991 и sin		0,0136	0,0136. Матрица
поворота
	0,99991		0,0136		0			0,99991	0,0136	0
H	0,0136		0,99991		0	, тогда H T		0,0136	0,99991	0 .
	0			0	1			0	0	1

Шаг 5. Находим A :

		0,99991			0,0136		0		1,98107		0,10932				0	0,99991			0,0136			0
	Anew		0,0136 0,99991				0		0,10932		10,01496			0,01063		0,0136			0,99991			0
			0		0		1			0	0,01063			4,00397			0			0		1
			1,97958			0			0,00014
			0		10,01645				0,01062 .
			0,00014		0,01062				4,00397
	Шаг 6. Умножим предыдущую матрицу U на новую матрицу поворота:
	0,99531		0		0,09674			0,99991			0,0136		0		0,99522		0,01354			0,09674
U	0,00482		0,99876		0,04958				0,0136		0,99991		0		0,00877		0,99873			0,04958 .
	0,09662		0,04981		0,99407				0		0		1		0,09729		0,04850			0,99407
	Приближение 4
	Шаг 1. Максимальный по модулю элемент верхней части a23																		0,01062.

	Шаг 2. Условие				0,01062			0,001 не выполнено.
	Шаг 3. Находим a22					10,01645, a33					4,00397. Угол поворота
	0,5arctg			2	0,01062					0,00177.

				10,01645		4,00397
	Шаг 4. Находим cos 0,00177									0,99999		1 и sin 0,00177					0,00177. Матрица
поворота
		1		0		0						1			0		0
	H	0	0,99999		0,00177 , тогда H T							0		0,99999		0,00177 .
		0	0,00177		0,99999							0		0,00177		0,99999
	Шаг 5. Находим A :
		1		0		0			1,97958				0		0,00014		1		0				0
	Anew	0		0,99999		0,00177				0	10,01645				0,01062		0	0,99999				0,00177
		0		0,00177		0,99999				0,00014		0,01062			4,00397		0	0,00177			0,99999
			1,97958			0			0,00014
			0		10,01647					0	.
			0,00014			0			4,00395
	Шаг 6. Снова умножим предыдущую матрицу U на новую матрицу пово-
рота:
	0,99522		0,01354		0,09674				1		0			0		0,99522				0,01371			0,09671
U	0,00877		0,99873		0,04958				0	0,99999			0,00177			0,00877			0,99864				0,05134 .
	0,09729		0,04850		0,99407				0	0,00177		0,99999				0,09729				0,05025			0,99399

Приближение 5
Шаг 1.	Максимальный по модулю элемент верхней части a13 0,00014.
Шаг 2.	Условие		0,001 выполнено. Действия закончены.
Шаг 2.	Условие	0,00014	0,001 выполнено. Действия закончены.
Ответ. С погрешностью, не превышающей 0,001, собственные числа мат-
рицы 1 1,980; 2 10,016; 3			4,004.	Соответствующие им собственные век-
торы
		0,995		0,014	0,097
	U1	0,009 ,	U2	0,999 , U3	0,051 .
		0,097		0,050	0,994

Замечание. Сравнивая матрицы A , полученные в 3-м и 4-м приближении, можно заметить, что максимальное изменение элементов не превышает 2 10 5 , а для матриц U не превышает 2 10 3 . Кроме того, максимальный по модулю элемент верхней части матрицы A почти не превышает 10 4 . Поэтому с одной со-

мнительной	цифрой	можно	считать,	что собственные числа матрицы
1 1,97958,	2 10,01647, 3		4,00395, а соответствующие им собственные век-
торы
		0,99522		0,01371	0,09671
	U1	0,00877 , U2		0,99864 , U3	0,05134 .
		0,09729		0,05025	0,99399

Пример показывает, что решение даже небольшой задачи и с невысокой точностью может быть долгим. Иногда действия удобно прекращать, сравнивая результаты приближений и оценивая по ним точность решения.

Пример 3. Найдём собственные числа и векторы матрицы

5 1 2

A 1 6 3 . 2 3 4

Приближение 1

Шаг 1. Максимальный по модулю элемент верхней части матрицы A – это a23 3.

Шаг 2. Точность не задана, однако очевидно, что прекращать действия рано.

Шаг		3.	Находим	a22 6, a33 4	и	угол	поворота
0,5arctg	2	3	0,6245.
0,5arctg	6	4	0,6245.
	6	4
				59

Шаг 4. Находим cos 0,6245 0,8112 и sin 0,6245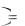 0,5847и составляем матрицу поворота

	1	0	0		1	0	0
H	0	0,8112	0,5847	, при этом H T	0	0,8112	0,5847 .
	0	0,5847	0,8112		0	0,5847	0,8112

Шаг 5. Находим

			1	0		0	5	1	2	1		0			0
	Anew		0	0,8112		0,5847 1		6	3	0	0,8112			0,5847
			0	0,5847		0,8112	2	3	4	0	0,5847			0,8112		.
																.
				5		0,3582	2,2072
			- 0,3582		8,1623		0
			2,2072			0	1,8377
Это новая матрица A .
						1	0		0
	Шаг 6. Находим U 0						0,8112		0,5847	– в 1-м приближении совпадает с 1-й Н.
						0	0,5847		0,8112
	Приближение 2.
	Шаги 1 - 2. Максимальный по модулю элемент верхней части матрицы A
−число a13		2,2072. Оно слишком велико, чтобы прекратить вычисления.
	Шаг			3.		Находим		a11 5, a33				1,8377и			угол		поворота
	0,5arctg	2	2,2072		0,4509.
	0,5arctg	5	1,8377		0,4509.
		5	1,8377
	Шаг 4. Находим cos 0,4509							0,9 и sin 0,4509				0,4358 . Составляем матрицу по-
ворота
	0,9		0	0,4358					0,9			0	0,4358
H	0		1	0		, тогда H T			0			1			0	.
	0,4358		0	0,9					0,4358			0			0,9
	Шаг 5. Находим новую матрицу A :
				0,9	0	0,4358		5	0,3582			2,2072			0,9	0	0,4358
	Anew			0	1	0	- 0,3582		8,1623			0			0	1	0
			0,4358		0	0,9	2,2072		0			1,8377			0,4358	0	0,9
			6,1304			0,3224	0,1283
			- 0,3224			8,1623	0,1561
				0,1283		0,1561	0,7067

<<< < Предыдущая 1 2 3 4 56 / 86 7 8 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
13.11.20221.73 Mб25526.pdf
#
13.11.20221.73 Mб25527.pdf
#
13.11.20221.73 Mб15528.pdf
#
13.11.20221.75 Mб25529.pdf
#
13.11.20221.75 Mб25530.pdf
#
13.11.20221.75 Mб25531.pdf
#
13.11.20221.75 Mб15532.pdf
#
13.11.20221.76 Mб25533.pdf
#
13.11.20221.76 Mб15534.pdf
#
13.11.20221.76 Mб05535.pdf
#
13.11.20221.77 Mб25536.pdf