
5531
.pdf
1 |
b1 |
0 |
0 |
|
0 |
|
x1 |
f1 |
|
|
a2 |
1 b2 |
0 |
|
0 |
|
x2 |
f2 |
|
||
0 |
a3 |
1 |
b1 |
|
0 |
|
x3 |
f3 |
. |
|
|
|
|
|
|
||||||
|
||||||||||
0 |
0 |
an-1 |
1 bn-1 |
xn 1 |
fn 1 |
|
||||
0 |
0 |
0 |
|
0 an |
1 xn |
fn |
|
|||
|
|
|
Идея метода прогонки состоит в следующем. |
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
Очевидно, |
что если |
x1 , x2 , , xn |
– набор конечных чисел, а в нашем |
||||||||||||||||||||||||||||
случае – |
решение |
системы, |
то |
можно |
|
подобрать |
такие |
наборы чисел |
||||||||||||||||||||||||||
1 , 2 , , |
n |
|
и |
|
1 , |
|
2 , n |
, |
что для каждой пары |
|
xk , xk 1 |
будет выполнено |
||||||||||||||||||||||
соотношение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xk |
|
k |
1 xk |
1 |
|
k 1 |
|
|
|
|
|
|
|
|
|||
или, что то же самое, для пары |
xk 1 , xk |
будет выполнено соотношение |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xk |
1 |
|
|
k xk |
|
|
k . |
|
|
|
|
|
|
|
(4.1) |
||
Подставив это соотношение в k-е уравнение ak xk |
1 |
xk |
bk xk 1 |
f k , |
|
|||||||||||||||||||||||||||||
получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
ak |
|
k xk |
|
|
k |
|
|
xk |
bk xk 1 |
f k , |
|
|
|
|
|
|
|||||
откуда xk |
|
|
|
bk |
|
xk 1 |
|
fk |
|
ak |
k |
|
. Таким образом, |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
ak |
k |
1 |
|
|
ak |
k |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
bk |
|
|
и |
|
|
|
fk |
ak |
k |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
1 |
|
ak |
|
1 |
|
k |
1 |
|
ak |
|
|
1 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
k |
|
|
|
|
|
|
|||||||
|
|
|
Поскольку |
|
|
из |
|
1-го |
уравнения |
|
x1 |
b1 x2 |
|
f1 |
можно |
выразить |
||||||||||||||||||
x1 |
b1 x2 |
f1 , получаем |
2 |
|
b1 и |
2 |
|
f1 . |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
Коэффициенты b1 |
и |
f1 |
известны; зная их, находим |
2 |
и |
2 ; затем по фор- |
|||||||||||||||||||||||||
мулам пересчёта находим |
3 |
и |
3 |
и так до |
|
n и |
n |
включительно. Заметим, что |
||||||||||||||||||||||||||
1 , |
1 |
для решения не нужны. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
В силу представления (4.1) необходимо знать xn , чтобы найти xn 1 и затем |
|||||||||||||||||||||||||||||||
все переменные до |
x1 включительно. |
Чтобы найти |
xn , в последнее уравнение |
|||||||||||||||||||||||||||||||
an xn 1 |
|
xn |
|
fn подставим xn |
1 |
|
n xn |
|
|
n . |
Получив |
an |
n xn |
n |
xn |
f n , нахо- |
||||||||||||||||||
дим x |
|
|
fn |
|
an |
n |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
n |
an |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
31

4.2. Общая схема решения системы уравнений методом прогонки сле-
дующая:
1. Разделить каждое уравнение на свой диагональный коэффициент;
2. Найти 2 |
|
b1 |
и |
2 |
f1 ; |
|
|
|
|
|
|
|
|
|
||
3. Найти |
|
|
|
|
bk |
|
и |
|
|
fk |
ak |
|
k |
для k |
2,3, , n |
1; |
k |
1 |
|
ak k |
1 |
k 1 |
|
ak |
|
1 |
|||||||
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
k |
|
|
|
||||||
Надо выполнить следующие действия: |
|
|
||||||||||||||
4. Найти x |
|
|
fn |
an |
n |
; |
|
|
|
|
|
|
|
|
|
|
n |
|
an |
|
1 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|||
5. Найти xk |
|
|
k |
1 xk |
1 |
k 1 |
для k |
n 1,n 2, ,1 . |
|
|||||||
Замечание. Традиционная ошибка, особенно при решении в EXCEL – на |
||||||||||||||||
последнем шаге вместо рекурсивной формулы |
xk |
k 1 xk 1 k 1 пользоваться |
||||||||||||||
неверным соотношением x |
|
fk |
ak |
k |
. |
|
|
|||||||||
k |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
ak |
k 1 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||||||
Из формул видно, что для решения методом прогонки надо, чтобы для |
||||||||||||||||
всех k от 2 до n выполнялось условие ak k 1 . Это неравенство гарантированно |
||||||||||||||||
выполняется, если одновременно:
а) b1 1 и an 1 , причём хотя бы одно неравенство строгое;
б) для всех k от 2 до n выполнено ak 
 bk 1.
bk 1.
Эти условия достаточны, но не необходимы: метод прогонки сходится и для некоторых систем, где условия нарушены.
Пример. Решим методом прогонки систему уравнений
|
|
5x1 4 x2 |
5, |
|
|
2 x1 5x2 x3 |
1, |
|
|
x2 2 x3 |
2. |
Решение. |
1-й шаг: Разделим 1-е уравнение на a11 5 , 2-е на a22 5 и 3-е |
||
на a33 2 , получим |
|
|
|
x1 0,8x2 |
1, |
|
|
0,4x1 x2 |
0,2x3 |
0,2, |
|
0,5x2 |
x3 |
1 |
|
или в матричном виде
32

1 |
0,8 |
0 |
x1 |
1 |
0,4 |
1 |
0,2 |
x2 |
0,2 . |
0 |
0,5 |
1 |
x3 |
1 |
|
2-й шаг: Из 1-го уравнения |
2 |
0,8, |
2 |
1 . |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
3-й шаг: |
|
|
|
|
|
|
0,2 |
|
|
|
|
|
|
0,2 |
|
|
5 |
и |
|
0,2 |
0,4 1 |
|
0,2 |
|
|
5 |
. |
|||||
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
0,4 |
0,8 |
1 |
|
|
|
|
|
0,68 |
|
17 |
0,4 |
0,8 |
1 |
0,68 |
|
17 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
4-й шаг: |
x3 |
|
1 |
0,5 |
5 /17 |
|
|
|
1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
0,5 |
5 /17 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
5-й шаг. |
x2 |
|
5 |
1 |
|
5 |
|
|
|
0 , затем x1 |
|
0,8 0 |
1 |
1 . |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
17 |
|
17 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
Ответ: x1 |
1, |
|
|
x2 |
0, x3 |
1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
З а м е ч а н и е. Пример носит демонстрационный характер. Разумеется, |
||||||||||||||||||||||||||||||||
здесь |
достаточно |
выразить |
x1 |
1 |
|
|
0,8x2 |
и |
|
x3 |
1 0,5x2 |
и |
подставить |
во |
|
2-е |
|||||||||||||||||
уравнение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
0,4 1 0,8x2 |
|
x2 |
0,2 |
1 |
0,5x2 |
|
0,2 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
откуда |
0,58x2 |
0,2 |
0,2 |
и потому |
|
|
x2 |
0 и, |
следовательно, |
x1 |
1 0,8 |
0 |
1 |
и |
|||||||||||||||||||
x3 |
1 |
0,5 0 |
1. Метод прогонки эффективен для систем высокого порядка, |
а |
|||||||||||||||||||||||||||||
для 3-го порядка не применяется.
§5. Решение систем методом L-U разложения матрицы
5.1.Описание метода
Пусть дана система уравнений |
AX |
F , где определитель матрицы |
|||||||||
A отличен от нуля. Оказывается, в этом случае матрицу можно представить |
|||||||||||
в виде произведения двух треугольных матриц, а именно, в виде |
|
||||||||||
a11 |
a12 |
a1n |
1 0 |
0 |
u11 |
u12 |
u1n |
|
|||
a21 |
a22 |
a2n |
l21 |
1 |
0 |
0 |
u22 |
u2n . |
(5.1) |
||
|
|
|
|
|
|
|
|
|
|
|
|
an1 |
an 2 |
ann |
ln1 |
ln 2 |
1 |
0 |
0 unn |
|
|||
Особенность 1-й матрицы в произведении (обозначим её буквой L) – в том, что все элементы её главной диагонали равны единице, все элементы над главной диагональю равны нулю, и только элементы под главной диагональю – числа, зависящие от матрицы A.
Во 2-й матрице (обозначим её как U), наоборот, равны нулю все элементы под главной диагональю, а на самой диагонали и выше её элементы зависят от A.
33

При этом не исключается, что какие-то из элементов lij или uij , из
(5.1) также равны нулю.
Обозначения L и U происходят от слов Lower (нижняя) и Upper
(верхняя). |
|
Если в системе AX F матрица A представлена в виде (5.1), |
то есть |
как произведение A LU , то систему можно записать в виде L U |
X F , |
или L U X F , что то же самое. |
|
Но U  X по правилам произведения матриц – некоторый столбец Z. Столбец X неизвестен (именно его мы пытаемся найти), тогда Z также неизвестен. Приходим к системе L
X по правилам произведения матриц – некоторый столбец Z. Столбец X неизвестен (именно его мы пытаемся найти), тогда Z также неизвестен. Приходим к системе L  Z F относительно столбца Z:
Z F относительно столбца Z:
AX F |
LU X F |
L UX |
F LZ |
F , где UX Z . |
|
Тем самым решение системы AX |
F можно свести к трём действиям: |
||||
1) |
представить матрицу A в виде произведения A |
LU ; |
|||
2) |
решить систему LZ |
F относительно столбца Z; |
|||
3) |
решить систему UX |
Z относительно столбца X. |
|||
Смысл метода состоит в том, что решить две треугольные системы уравнений намного проще, чем одну обычную той же размерности. Разложение мат-
рицы на треугольные множители также не представляет особых трудностей. |
|
||||||||||||||||
|
Посмотрим в общем виде, как разложить матрицу на множители. |
|
|||||||||||||||
|
Пусть |
для |
известных |
элементов |
aij |
матрицы |
A |
надо найти числа |
|||||||||
l21 , l31 , , ln,n 1 |
и u11 , u12 , , unn , чтобы выполнялось матричное равенство (5.1). За- |
||||||||||||||||
пишем его так: |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
1 0 0 |
u11 |
u12 |
u1n |
a11 |
a12 |
a1n |
|
|||||||
|
|
|
l21 |
1 |
0 |
0 |
u22 |
u2n |
a21 |
a22 |
a2n . |
(5.2) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
ln1 |
ln 2 1 |
0 |
0 unn |
an1 |
an 2 ann |
|
||||||||
|
Будем по очереди умножать строки матрицы L на столбцы матрицы U и |
||||||||||||||||
приравнивать к соответствующим элементам матрицы A. |
|
|
|
||||||||||||||
|
1. Произведение 1-й строки L и 1-го столбца U показывает, что u11 |
a11 . |
|||||||||||||||
Умножая остальные |
строки |
L на 1-й столбец U, |
получаем, что l21u11 |
a21 , |
|||||||||||||
l31u11 |
a31 , |
и |
так |
до |
|
ln1u11 |
an1 , |
откуда |
соответственно |
||||||||
l21 |
a21 |
, l31 |
a31 |
, , ln1 |
|
an1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
u11 |
u11 |
|
|
u11 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
34 |
|
|
|
|
|
|

2. Произведение 1-й строки L и 2-го столбца U показывает, что u12 a12 . Умножая 2-ю строку L на 2-й столбец U, получаем, что l21u12 u22 a22 , откуда u22 a22 l21u12 . В этом отличие от предыдущего пункта – найдя u12 , сразу находим и элемент под ним, т.е. u22 .
Затем, умножая следующие строки L на 2-й столбец U, получаем уравнения, из которых находим l32 , l42 , , ln 2 , а именно:
l31u12 |
l32u22 |
a32 |
l32 |
1 |
|
|
a32 |
|
|
l31u12 |
; |
|
|
|||||
|
|
|
|
|
|
|
|
|||||||||||
u22 |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
l41u12 |
l42u22 |
a42 |
l42 |
1 |
|
|
a42 |
|
|
l41u12 |
; |
|
|
|||||
|
|
|
|
|
|
|
|
|||||||||||
u22 |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
… |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ln1u12 |
ln 2u22 |
an 2 |
ln 2 |
1 |
|
|
an 2 |
|
|
ln1u12 . |
|
|
||||||
|
|
|
|
|
|
|
|
|||||||||||
|
u22 |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3. Из произведения 1-й строки L и 3-го столбца U получаем u13 |
a13 . Далее |
|||||||||||||||||
при помощи 2-й и 3-й строк L находим u23 |
и u33 : |
|
|
|
|
|
|
|
|
|
||||||||
l21u13 |
u23 |
a23 u23 a23 |
l21u13 ; |
|
|
|
|
|
|
|
||||||||
l31u13 |
l32u23 |
u33 |
a33 |
u33 |
|
|
a33 |
|
|
l31u13 |
l32u23 . |
|
||||||
теперь, умножая 4-ю и последующие строки L на всё тот же 3-й столбец, |
||||||||||||||||||
из получаемых уравнений находим l43 , l53 , , ln3 : |
|
|
|
|
|
|
|
|
|
|||||||||
l41u13 |
l42u23 |
l43u33 |
a43 |
|
l43 |
|
|
1 |
|
|
|
a43 |
l41u13 |
l42u23 |
; |
|||
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
u33 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
l51u13 |
l52u23 |
l53u33 |
a53 |
|
l53 |
|
|
1 |
|
|
|
a53 |
l51u13 |
l52u23 |
; |
|||
|
|
|
|
|
|
|
|
|||||||||||
|
|
u33 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
… |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ln1u13 |
ln 2u23 |
ln3u33 |
an3 |
|
ln3 |
1 |
|
|
an3 |
ln1u13 |
ln 2u23 . |
|||||||
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
u33 |
|
|
|
||||
4.Таким же образом при помощи каждого k-го столбца матрицы U находим вначале u1k , u2k , , ukk , а затем lk 1,k , lk 2,k , , lnk .
5.На последнем шаге находим только элементы последнего столбца U. Разложение матрицы выполнено.
Теперь запишем систему LZ |
F : |
|
|
|
|
|
|
|
|||
1 |
0 |
0 |
z1 |
f1 |
z |
f , |
|
|
|
|
|
l21 |
1 |
0 |
z2 |
f 2 |
l 1 |
z 1 |
z |
2 |
f |
2 |
, |
|
|
|
|
|
21 1 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
ln1 |
ln2 1 |
zn |
f n |
ln1z1 ln2 z2 zn f n . |
|||||||
|
|
|
|
|
|
|
|||||
35

Из |
1-го |
уравнения сразу |
z1 |
f1 . Затем из 2-го |
уравнения |
|
находится |
||||||||||||||||||||||||
z2 |
f2 l21z1 , |
|
далее из 3-го |
уравнения находим |
z3 |
f3 |
l31 z1 |
l32 z2 , и |
т.д. |
||||||||||||||||||||||
Наконец, |
из последнего уравнения получаем zn |
|
fn |
ln1 z1 |
ln 2 z2 |
|
lnn |
1 zn 1 . |
|||||||||||||||||||||||
Столбец Z получен. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
Из системы U X |
|
Z надо найти столбец X. Запишем подробно: |
||||||||||||||||||||||||||||
|
|
u11 |
u12 u1n |
x1 |
|
z1 |
|
u11 x1 |
u12 x2 |
u1n xn |
z1, |
|
|||||||||||||||||||
|
|
0 |
|
u22 |
u2n |
x2 |
|
z2 |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
u |
22 |
x |
2 |
u |
2n |
x |
n |
z |
2 |
, |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
0 |
|
0 |
unn |
xn |
|
zn |
|
|
|
|
|
|
|
|
|
unn xnn |
zn . |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Из последнего уравнения имеем, что |
x |
|
zn |
|
|
. Из предпоследнего урав- |
|||||||||||||||||||||||||
n |
unn |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
нения u |
|
x |
|
u |
|
x |
|
z |
|
находится x |
|
zn 1 |
|
|
un 1,n xn |
, и т.д., пока из 1-го |
|||||||||||||||
|
|
|
n |
n 1 |
n 1 |
|
|
|
|
||||||||||||||||||||||
|
n 1,n 1 |
|
n 1 n 1,n |
|
|
|
|
|
|
un 1,n 1 |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
уравнения не получим, что |
x1 |
1 |
z1 |
u12 x2 |
u13 x3 |
|
u1n xn . |
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||
u11 |
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Тем |
самым |
получим |
решение |
исходной |
системы |
в |
виде набора |
|||||||||||||||||||||||
x1 ; x2 ; xn .
Все действия легко программируются и не требуют поиска какихлибо упрощающих тонкостей, как, например, в методе Гаусса или в методе подстановки.
|
5.2. Общая схема решения системы методом L-U разложения |
||||||||||||||
|
|
1-й шаг: поиск матриц-множителей L и U. |
|
|
|
|
|
||||||||
Для каждого столбца с номером j, где j меняется от 1 до n, |
|
|
|
||||||||||||
|
|
|
|
1) |
находим u1 j |
a1 j ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
2) |
по |
всем |
строкам |
с |
номерами |
i от |
2 |
до |
j |
находим |
|
|
|
|
i |
1 |
|
|
|
|
|
|
|
|
|
|
|
uij |
aij |
lik ukj |
; |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
k |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3) |
по |
всем строкам |
с |
номерами |
i |
от |
j+1 |
до |
n |
находим |
|
|
1 |
|
|
j 1 |
|
|
|
|
|
|
|
|
|
|
|
lij |
|
aij |
lik ukj . |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
u jj |
k 1 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
2-й шаг: вычисление элементов столбца Z. |
|
|
|
|
|||||||||
|
|
|
|
1) |
z1 |
f1 ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
2) |
для всех k от 2 до n находим zk |
fk |
lk1z1 |
lk 2 z2 |
lk ,k 1zk 1 . |
||||||
|
|
|
|
|
|
|
|
36 |
|
|
|
|
|
|
|

|
3-й шаг: вычисление элементов столбца X. |
|
|
|
|
|
||||||||||
|
|
1) x |
|
|
zn |
; |
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
unn |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
2) |
|
|
для |
k |
от |
|
n |
1 |
до |
1 |
находим |
|||
xk |
1 |
zk uk ,k 1 xk 1 uk ,k 2 xk 2 |
|
ukn xn . |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
||||||||
ukk |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример 1. Решим методом L-U разложения систему 2-го порядка |
|
||||||||||||||
|
|
|
|
|
|
|
|
5 x |
6 y |
8, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 x |
9 y |
10. |
|
|
|
|
|
|
|
Решение. |
|
Здесь A |
5 |
6 , F |
|
8 . |
Найдём матрицы L |
1 |
0 |
и |
|||||
|
|
|
|
|
|
|
7 |
9 |
10 |
|
|
|
l21 |
1 |
|
|
U |
u11 |
u12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
u22 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Не придерживаясь строгой схемы, посмотрим идею метода. Из произведения
1 |
0 |
u11 |
u12 |
5 |
6 |
l21 |
1 |
0 |
u22 |
7 |
9 |
получаем систему из четырёх уравнений и решаем её:
u11 |
5, |
|
u11 |
5, |
u11 |
5, |
u11 |
5, |
u12 |
6, |
|
u12 |
6, |
u12 |
6, |
u12 |
6, |
l21u11 |
7, |
5l21 |
7, |
l21 |
1,4, |
l21 |
1,4, |
|
l21u12 |
u22 9 |
6l21 |
u22 9 |
6 1,4 |
u22 9 |
u22 |
0,6. |
|
Значит, исходную систему можно записать в виде
|
1 |
0 |
5 |
6 |
x |
8 . |
|
|
1,4 |
1 |
0 |
0,6 |
y |
10 |
|
Обозначим произведение |
5 |
6 |
x |
как неизвестный столбец |
|||
0 |
0,6 |
y |
|||||
|
|
|
|
||||
тогда получается система |
1 |
0 |
s |
8 |
. Записав её в виде уравнений |
||
|
1,4 |
1 |
t |
10 |
|
|
|
st ,
1s 0t 8,
1,4s 1t 10,
сразу видим, что s 8 , и тогда t 10 1,4  8
8 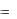 1,2 .
1,2 .
Теперь, вспомнив происхождение неизвестных s и t, решаем систему
37

5 |
6 |
x |
8 |
|
5 x |
6 y 8, |
|
, т.е. |
|
|
|
||||
0 |
0,6 |
y |
1,2 |
0 x |
0,6 y |
1,2. |
|
Из 2-го уравнения |
имеем, |
что |
y |
2 . Тогда |
из 1-го находим х: |
||
5x 6 2 8 5x 20 x 4 . |
|
|
|
|
|
||
Итак, решение системы – числа x |
4, y |
2 . |
|
||||
Обратите внимание, что вычислений столько же, сколько при решении методом подстановки или Крамера, и больше места заняли пояснения.
|
|
По общей схеме система решалась бы так: |
|
|
|
||||||||||||||||||
|
|
1) при помощи 1-го столбца матрицы U ( j |
|
1) |
|
||||||||||||||||||
|
|
|
1.1) |
u11 |
5 ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
1.2) |
других ui1 |
в 1-м столбце нет; |
|
|
|
|||||||||||||||
|
|
|
1.3) |
l |
|
|
|
1 |
7 |
0 |
1,4 ; |
|
|
|
|
|
|
|
|
||||
|
|
|
21 |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
2) при помощи 2-го столбца матрицы U ( j |
|
2 ) |
|
||||||||||||||||||
|
|
|
2.1) |
u12 |
6 ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
2.2) |
меняя i от 2 до j |
|
2 , находим u22 |
|
a22 l21u12 , т.е. |
|||||||||||||||
u22 |
9 |
1,4 |
6 |
0,6 ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
2.3) |
строк с номерами от 3 до 2 не существует; |
|||||||||||||||||||
|
|
3) ищем величины z1 , z2 : |
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
z1 |
f1 |
|
z1 |
8; |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
z2 |
f2 |
l21z1 |
|
|
z2 |
10 |
1,4 |
8 z2 |
1,2 ; |
|
|
|
|||||||
|
|
4) находим неизвестные: |
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
x2 |
z2 |
|
|
x2 |
|
|
1,2 |
|
x2 |
2 ; |
|
|
|
|
|||||
|
|
|
|
u22 |
|
|
|
|
0,6 |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
x |
1 |
|
z u x |
|
|
x |
|
1 |
8 6 |
2 |
x |
|
4 . |
||||||
|
|
|
|
|
|
|
2 |
|
|
2 |
|||||||||||||
|
|
|
|
1 |
u11 |
1 |
|
12 |
|
1 |
5 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
Ответ: x |
|
4, y 2 . |
|
|
|
|
|
|
|
|
|
|
|
||||||||
Разумеется, пример 1 носит демонстрационный характер. При разовом решении системы 2-го порядка метод L-U разложения не даёт никакого выигрыша ни в числе действий, ни в точности. Если же необходимо решить много систем с неизменными коэффициентами и меняющейся правой
38

частью, удобнее метод обратной матрицы. Намного актуальнее метод для систем высокого порядка.
Пример 2. Решим систему
2 x1 |
x2 3x4 |
9, |
|
|
4 x1 |
8x2 |
7 x3 |
5x4 |
3, |
6 x1 |
3x2 |
2 x3 10 x4 |
42, |
|
8x1 |
16 x2 |
59 x3 20 x4 36. |
||
Решение. Здесь также не будем придерживаться строгой схемы, а посмотрим идею решения. Более того, убедимся, что поиск элементов матриц U и L можно вести по строкам, а не столбцам.
|
2 |
1 |
0 |
3 |
|
9 |
|
4 |
8 |
7 |
5 |
|
3 |
Составляем матрицу A |
6 |
3 |
2 |
10 |
, записываем столбец F |
42 . |
|
8 |
16 |
59 |
20 |
|
36 |
Необходимо найти матрицы
|
1 |
0 |
0 |
0 |
|
|
u11 |
u12 |
u13 |
u14 |
|
l21 |
1 |
0 |
0 |
|
|
0 |
u22 |
u23 |
u24 |
L |
l31 |
l32 |
1 |
0 |
; |
U |
0 |
0 |
u33 |
u34 . |
|
l41 |
l42 |
l43 |
1 |
|
|
0 |
0 |
0 |
u44 |
Перемножим все строки матрицы L со всеми столбцами матрицы U. Полученные произведения приравняем к соответствующим элементам матрицы A по правилу
«произведение i-й строки и j-го столбца равно элементу aij ».
Получим 16 уравнений относительно 16 неизвестных l21 , l31 , , u34 , u44 .
1. Умножая 1-ю строку матрицы L на четыре столбца матрицы U, получаем, что
u11 2, u12 1, u13 0, u14 3 .
2. Умножая 2-ю строку матрицы L на столбцы матрицы U, получаем систему уравнений
39

l21u11 l21u12 l21u13 l21u14
1 0 4,
1 u22 8,
1 u23 7,
1 u24 5.
Подставив известные значения u11 , u12 , u13 , u14 , приходим к системе
2l21 |
4, |
|
|
|
l21 |
u22 |
8, |
|
|
u23 |
7, |
|
|
|
3l21 |
u24 |
5, |
|
|
из которой l21 2 u22 6, u23 7, u24 |
1 ; |
|
|
|
3. Умножая 3-ю строку матрицы L на столбцы матрицы U, получаем |
||||
систему |
|
|
|
|
l31u11 |
6, |
|
|
|
l31u12 |
l32 u22 |
3, |
|
|
l31u13 |
l32 u23 |
u33 |
2, |
|
l31u14 |
l32 u24 |
u34 |
10. |
|
Подставим сюда уже известные значения:
|
|
|
|
2l31 |
6, |
|
|
|
|
|
|
|
|
l31 |
6l32 |
3, |
|
|
|
|
|
|
|
0l31 |
7l32 |
u33 |
2, |
|
|
|
|
|
|
3l31 |
l32 u34 |
10. |
|
|
|
Тем самым l31 3 |
3 |
6l32 |
3 |
l32 |
1, но тогда 7 |
u33 2 u33 9 , а из 4- |
|||
го уравнения 3 3 |
1 |
u34 |
10 |
u34 0 . |
|
|
|
|
|
4. Умножая 4-ю строку матрицы L на столбцы матрицы U, получаем, что |
|||||||||
|
|
|
l41u11 |
8, |
|
|
|
|
|
|
|
|
l41u12 |
l42 u22 |
16, |
|
|
||
|
|
|
l41u13 |
l42 u23 |
l43u33 |
59, |
|
||
|
|
|
l41u14 |
l42 u24 |
l43u34 |
u44 |
20. |
||
Подставим все значения, найденные выше, получим
40
