5531

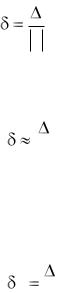
Чисел а, удовлетворяющих неравенству (2.1), будет бесконечное множество. Желательно найти наименьшую из верхних границ . На практике часто за а принимают не наименьшую из верхних граней Δ, а одну из верхних граней, достаточно близкую к наименьшей верхней грани.

Абсолютная погрешность и предельная абсолютная погрешность не характеризуют качество измерений. Действительно, если при измерении длины комнаты и расстояния от центра города до аэропорта допущена предельная абсолютная погрешность измерения в 1 см, то качество измерений совершенно различно. В первом случае его даже трудно признать удовлетворительным, тогда как во втором – высокой точности. Поэтому вводится ещё одна характеристика точности вычислений – относительная погрешность.

Относительной погрешностью δ называется отношение абсолют-

Так как точное значение величины обычно неизвестно, то δ вычисляется по приближённой формуле

Тогда за предельную относительную погрешность δа естественно принять отношение предельной абсолютной погрешности к модулю при-

Если измеряемая величина имеет размерность, то абсолютные погрешности имеют ту же размерность; относительные погрешности будут величинами безразмерными. Иногда предельную относительную погрешность выражают в процентах.

2.2. Десятичная запись приближённых значений чисел

Любое действительное (вещественное) число представляется в виде конечной или бесконечное десятичной дроби. Для единообразия записи конечные десятичные дроби будем дополнять справа бесконечной последовательностью

11

нулей; целые числа также будем дополнять бесконечной последовательностью нулей справа от запятой, поставленной после написания последней цифры цело-

го числа. Например, 0,125 и 15 запишутся так : 0,125 000...; 15,000... .

Тогда всякое неотрицательное число можно записать в виде b0,b1b2b3..., где b0 – целая часть этого числа, а 0,b1b2b3... – его дробная часть. Такое представление применяется и для отрицательных чисел, при этом целую часть этого чис-

При такой записи отрицательного числа целую часть этого числа называют его

характеристикой, а дробную – его мантиссой.

Пусть действительное неотрицательное число х в десятичной записи имеет вид х = а0,а1а2а3... . Тогда его приближением а по недостатку с точностью до единицы будет число а0, а по избытку – число а0 + 1. Далее, приближения с точностью до 10-n (n = 1, 2, 3, ...) по недостатку имеют вид а = а0,а1а2а3...аn, а по избытку – а = а0,а1а2а3...аn + 10-n. При этом в записи а опущены нули после последней цифры.

Если х = а0,а1а2а3 … есть отрицательное действительное число, то его десятичные приближения можно найти следующим образом. Надо будет найти десятичные приближения по недостатку и по избытку противоположного числа (−х). Тогда десятичными приближениями по недостатку числа х будут десятичные приближения по избытку числа (−х), взятые со знаком «минус», а десятичными приближениями по избытку для х будут десятичные приближения по недостатку числа (−х), также взятые со знаком «минус».

Разности между соответствующими десятичными приближениями по из-

тичных знаков после запятой.

Поясним сказанное двумя примерами. Для числа х = 5,317 2... с точностью до 1, до 0,1, до 0,01, до 0,001, до 0,000 1 приближениями по недостатку будут числа 5; 5,3; 5,31; 5,317; 5,317 2, а по избытку – числа 6; 5,4; 5,32; 5,318; 5,317 3.

12

Для отрицательного числа х = – 5,743…= 5,257 ... с точностью до 1, до 0,1, до 0,01, до 0,001 приближениями по недостатку будут числа – 6; – 5,8; – 5,75; – 5,744; а по избытку – числа -5; – 5,7; – 5,74; – 5,743.

Число а (приближение к х) желательно записывать так, чтобы, не используя форму записи х = а ± а, по десятичной записи а можно было судить о точности приближения. Для этого применяется понятие о верных цифрах числа а.

Цифра α в десятичной записи числа а (приближения к х) называется верной в широком смысле, если предельная абсолютная погрешность приближения не превосходит единицы того разряда, которомупринадлежит цифра α.

Поясним данное определение примерами.

Пусть х = 5,154 ± 0,000 9. Так как а = 0,000 9 < 0,001, то последняя цифра

4 числа а = 5,154 (приближённого значения х) верна в широком смысле. Очевидно, что верны и остальные цифры.

Пусть известно, что все цифры числа а = 5,342, являющегося приближением некоторого х, верны в широком смысле. Это означает, что предельная абсолютная погрешность а не превосходит 0,001.

Цифра α в десятичной записи числа а называется верной в строгом смысле, если предельная абсолютная погрешность приближения не превосходит половины единицы того разряда, которому принадлежит цифра α.

цифра 3 числа а верна в широком смысле (в этом смысле верны и цифры 7, 5, 6). В строгом же смысле верны только цифры 7, 5, 6. Последняя цифра 3 в строгом

а 2

Принято применять правило: при десятичной записи приближённого значения числа записываются только верные цифры. Это правило позволяет сразу говорить о предельной абсолютной погрешности.

Например, пусть в записях а, b, c приближённых значений некоторых своих величин все цифры верные: а = 0,382, b = 35,74, с = 12, 000 213. Если эти цифры верны в широком смысле, то а < 0,001, b < 0,01, с < 0,000 001. Если

13

при этом известно, что в записи этих же чисел оставлены цифры, верные в строгом смысле, то это означает, что а < 0,000 5, b < 0,005, с < 0,000 000 5.

Если в приближённой записи числа последние десятичные знаки есть нули, являющиеся верными цифрами, то это количество нулей в записи а нужно сохранить. В этом смысле записи а = 5,2 и а = 5,200 являются различными.

Первая означает, что а является приближением к х с точностью до 0,1. Вторая же означает, что а является приближением к х с точностью до 0,001.

Цифры в записи приближённого значения числа, о которых неизвестно, являются они верными или нет, называются сомнительными.

Значащими цифрами числа, записанного в виде десятичной дроби, называют все его верные цифры, начиная с первой слева, отличной от нуля.

Поясним это определение примерами. При этом будем считать, что в десятичной записи числа все цифры являются верными. Рассмотрим сле-

дующие числа: 525; 5,25; 0,005 25; 0,525; 0,525 00. Первые четыре числа имеют по три значащих цифры, последнее число – пять значащих цифр.

2.3.Округление чисел

Ввычислительной работе приходится действовать с числами, которые в десятичной записи имеют много значащих цифр. Иногда часть этих цифр целесообразно отбросить, заменяя их нулями. Эту операцию назы-

вают округлением чисел.

Пусть a* есть число, полученное в результате округления а. Тогда абсолютная величина разности а – а*, т.е. число а а* называется по-

грешностью округления. Естественно a* выбирать так, чтобы погреш-

ность округления была наименьшей.

Например, пусть число а = 523,72 требуется округлить до целого числа. Если в качестве а* взять число 523, то погрешность округления бу-

ло а* = 524.

Правило округления формулируется следующим образом: при округлении числа до n значащих цифр отбрасывают все цифры, стоящие справа от n-й значащей цифры, или, если это нужно для сохранения разря-

14

дов в случае целого числа, заменяют их нулями; при этом, если первая слева из отброшенных цифр больше или равна 5, то последнюю оставленную

цифру увеличивают на единицу. Поясним это правило примерами.

Пример 1. Число а = 3,65 есть приближённое значение некоторого числа х, причём все цифры в записи а верны. При округлении его до двух значащих

торого х его приближённое значение а = 2,34, то при округлении его до двух

разряда, определяемого последней оставленной значащей цифрой.

Пример 2. Пусть a, b, c, d, s таковы: а = 52, b = 56, c = 123, d = 129, s = 2 345, т.е. целые числа, причём все цифры являются верными. Тогда при округлении этих чисел до одной значащей цифры получим следующие результаты округлений: а* = 50, b* = 60, c* = 100, d* = 100, s* = 2 000. При округлении c, d, s

до двух значащих цифр имеем следующее: c* = 120, d* = 130, s* = 2 300. При округлении s до трёх значащих цифр имеем, что s* = 2 350.

Пример 3. Числа а = 0,0023 и b = 0,0038, все цифры в записи которых верны, требуется округлить до первой значащей цифры. Оба числа имеют по две значащие цифры. Первая значащая цифра у числа а есть 2, а у числа b – 3. Тогда а* = 0,002 и b* = 0,004.

Пусть х – точное значение числа, а – приближённое значение и а* – число, полученное в результате округления а. Оценим погрешность приближения к х в результате округления:

т.е. предельная абсолютная погрешность приближения а* к х (приближения после округления) не превосходит суммы предельной абсолютной погрешности приближения а к х и погрешности округления.

15

2.4. Погрешности результатов действий над приближёнными значениями чисел

Перейдём к вопросу об учёте погрешностей в результате арифметических действий над числами.

ствующие предельные абсолютные погрешности. Приближением к алгебраической сумме х = х1 + х2 (слагаемые могут быть числами любого знака) будет соответствующая алгебраическая сумма а = а1 + а2 с предельной абсолютной по-

т.е. предельная абсолютная погрешность алгебраической суммы приближений а1, а2 (к х1, х2) равна арифметической сумме предельных абсолютных погрешностей слагаемых. Утверждение справедливо для любого конечного числа слагаемых.

Пример 1. Пусть х1 = 32,46 ± 0,02, х2 = 41,27 ± 0,01. Тогда х1 + х2 = 73,73 ± 0,03 (Δа = 0,02 + 0,01 = 0,03), причём последняя цифра числа а =

73,73 не может считаться верной (сомнительная).

Пример 2. Даны а1 = 21,24 и а2 = 12,13, причём все цифры верны в широ-

ком смысле. Разность а = а1 – а2 = 21,24 – 12,13 = 9,11;

мнительная. Ответ только с одними верными цифрами будет 9,1.

Предельная относительная погрешность произведения и частного двух, отличных от нуля, приближений а1 и а2 равна сумме предельных относительных погрешностей этих чисел:

Можно считать, что х1 х2 = 16,95 ± 0,09 (последняя цифра 5 является сомнительной).

Пример 4. Пусть х1 ≈ а1 = 3,18 и х2 ≈ а2 = 2,42, причём все значащие циф-

ры верны в широком смысле. Надо найти приближение к числу х1 и точность

х2

Следовательно,

Перейдём к изучению погрешностей при возведении числа в степень с натуральным показателем n и при извлечении корня n-ой степени из числа.

Предельная относительная погрешность числа аn равна произведению показателя степени на предельную относительную погрешность основания, т.е.

Предельная относительная погрешность числа n a равна предельной относительной погрешности подкоренного числа а, делённой на n:

Пример 5. Пусть х ≈ а = 1,4, причём у числа а все значащие цифры верны в широком смысле. Надо найти число х3. Имеем а3 = (1,4)3 = 2,744. Так как а =

Учитывая погрешность округления а3 = 2,744 до 0,1, получим, что х3 = 2,7 ± 0,6.

Пример 6. По данным предыдущего примера надо найти 3 х . Так как δа ≈

0,07, то, согласно (2.8),

Можно считать, что 3 х =1,12 ± 0,02.

§ 3. Итерационные методы решения систем линейных алгебраических уравнений

3.1. Общая постановка задачи

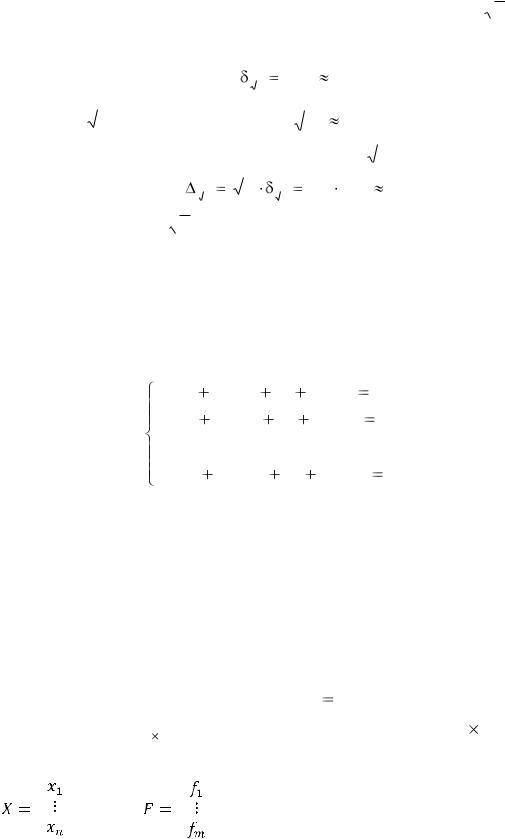
Системой линейных алгебраических уравнений (СЛАУ) называют систему вида

n) при неизвестных и правыми частями bi (i=1,…, m). Все неизвестные x j , ко-

эффициенты aij и правые части bi считаются действительными числами. Обыч-

но предполагают, что число уравнений в системе (3.1) не превосходит числа не-

18

Если в системе (3.1) число уравнений будет равно числу неизвестных m n, то матрица А системы будет квадратной матрицей n – го порядка ( n n −его размерность), а матрица F будет иметь размерность n 1.

Решать систему (3.1) – значит найти числа x1 , x2 , , xn , при которых все равенства системы (3.1) обращаются в тождества.

На первом курсе в дисциплине «Линейная алгебра» изучают точные методы решения СЛАУ – метод Крамера, метод Гаусса, метод Гаусса – Жордана, метод обратной матрицы. При этом метод Крамера и метод обратной матрицы применяются только для систем с квадратными матрицами, а метод Гаусса и Гаусса – Жордана применяются как для случая m n , так и для случая m n .

Метод Крамера и обратной матрицы дают понятные и хорошо запоминающиеся алгоритмы решения систем с квадратными матрицами, определитель которых отличен от нуля (такие системы называют крамеровскими). Однако при большом числе уравнений эти методы весьма неэкономичны, неудобны при работе на компьютере и опасны накоплением погрешности.

Решение методом Гаусса предпочтительнее, особенно когда нет необходимости решать одну и ту же систему с меняющейся правой частью. Кроме того, только метод Гаусса позволит исследовать систему, в которой число уравнений меньше числа неизвестных. В любой ситуации (m ≤ n) этим методом из исходной системы исключаются лишние уравнения, то есть полученные в результате элементарных преобразований уравнением вида

0 x1 0 xn 0 ,

которые выполняются при любых наборах неизвестных и, следовательно, из системы должны быть удалены.

Тем не менее метод Гаусса также накапливает погрешность и становится неэкономичен для реальных систем из тысяч уравнений, а именно такие системы возникают при решении прикладных задач.

К счастью, системы в прикладных задачах отличаются не только огромным объёмом, но и такими особенностями, как разрежённость и диагональное преобладание. Именно это позволяет решить систему быстрее и экономичнее.

19

то есть в каждой строке элемент на главной диагонали по модулю больше, чем сумма всех остальных элементов (также взятых по модулю). При выполнении условия (3.3) система уравнений (3.2) с квадратной матрицей А называется си-

стемой с диагональным преобладанием независимо от правой части F.

Под разреженностью системы понимают наличие большого числа нулевых элементов в стороне от главной диагонали матрицы.

3.2. Метод простой итерации

Перепишем систему в виде

Если A – матрица с диагональным преобладанием, то в каждой строке C сумма модулей коэффициентов меньше единицы. Тогда последовательность

20