
5531
.pdf
|
|
|
|
|
|
x k 1 |
|
c x k |
|
c x k |
c |
|
x k , |
|
|||||||||
|
|
|
|
|
|
1 |
|
12 |
2 |
|
13 3 |
|
|
1n |
n |
|
|
||||||
|
|
|
|
|
|
x k 1 |
c |
|
x k |
c |
23 |
x k |
c |
2n |
x k , |
|
|
||||||
|
|
|
|
|
|
2 |
|
21 1 |
|
3 |
|
|
|
n |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x k 1 |
|
c |
x k |
|
c |
n2 |
x k |
c |
nn 1 |
x k |
. |
||||||
|
|
|
|
|
|
n |
|
|
n1 1 |
|
|
2 |
|
|
|
n 1 |
|
||||||
С некоторого момента оказывается, что |
X k |
1 |
X k − с некоторой точностью, ко- |
||||||||||||||||||||
торую следует указать заранее. Тогда, если |
|
– необходимая точность, действия |
|||||||||||||||||||||
прекращают, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1,2, , n |
|
1 x k |
1 |
|
|
|
|||||||||||||||
а)или когда для всех i |
выполнено |
x k |
|
; |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
i |
|
|
|
|
|
б)или когда |
|
xik |
1 |
xik |
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
в)или когда |
|
x k |
1 |
x k |
2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
i |
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Последнее условие удобно проверять при программировании вычислений. |
|||||||||||||||||||||||
Пример 1. Решим с точностью 0,01 систему |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
x 0,1y |
|
|
|
0,6; |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
0,3x |
y |
|
|
1. |
|
|
|
|
|
|
|
|
||||
Решение. Коэффициенты на главной диагонали равны 1. Достаточное |
|||||||||||||||||||||||
условие (3.3) сходимости выполнено: 1 |
|
0,1; 1 |
0,3. |
|
|
|
|
|
|||||||||||||||
Запишем систему в виде |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
x |
|
0,1y |
|
0,6, |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
y |
|
0,3x |
|
1. |
|
|
|
|
|
|
|
||||
Взяв x0 0, y0 |
|
0 , находим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
x1 |
0,1 0 0,6 |
0,6; |
|
|
|
|
|
||||||||
y1  0,3 0 1 1.
0,3 0 1 1.
Продолжим подстановку, оставляя три знака после запятой.
x2 |
0,1 |
1 0,6 |
0,5; |
а) |
|
|
|
y2 |
0,3 |
0,6 1 |
0,82; |
x3  0,1 0,82 0,6 0,518;
0,1 0,82 0,6 0,518;
б)
y3  0,3 0,5 1 0,85;
0,3 0,5 1 0,85;
x4  0,1 0,85 0,6 0,515;
0,1 0,85 0,6 0,515;
в)
y4  0,3 0,518 1 0,847;
0,3 0,518 1 0,847;
21

x1 |
0,1 |
0,847 |
0,6 |
0,515; |
|
|
|
|||||
г) |
|
|
|
|
|
|
|
|
|
|
|
|
y1 |
0,3 |
0,515 |
1 |
|
0,846. |
|
|
|
|
|||
Последний шаг необязателен, поскольку уже |
x4 |
x3 |
|
0,01 и |
y4 y3 |
0,01 . |
||||||
Ответ. С точностью 0,01 решение системы – x = 0,52 и y = 0,85. |
||||||||||||
Пример 2. Решим с точностью 0,01 систему |
|
|
|
|
||||||||
10 x |
2 y |
3z |
11, |
|
|
|
|
|
|
|||
x |
25 y |
2 z |
53, |
|
|
|
|
|
|
|||
3x |
2 y |
20 z |
19. |
|
|
|
|
|
|
|||
Решение. Достаточное условие (3.3) сходимости выполнено: |
||||||||||||
10 |
|
2 |
3; 25 |
1 |
2; 20 |
3 |
2 . |
|
|
|||
Выражая x, y, z из соответствующих уравнений, получим равносильную систему
|
|
x |
0,1 11 2 y 3z |
, |
|
||
|
|
y |
0,04 53 x 2z , |
|
|||
|
|
z |
0,05 |
19 3x |
2 y . |
|
|
Итерационная последовательность |
|
|
|
|
|
||
|
|
x k |
1 |
0,2 y k |
0,3z k |
1,1, |
|
|
|
y k |
1 |
0,04 x k |
|
0,08 z k 2,12, |
|
|
|
z k |
1 0,15 x k |
0,1y k |
0,95 |
||
или, в матричном виде, |
|
|
|
|
|
|
|
x k |
1 |
0 |
0,2 |
0,3 |
|
x k |
1,1 |
y k |
1 |
0,04 |
0 |
0,08 |
|
y k |
2,12 . |
z k |
1 |
0,15 |
0,1 |
0 |
|
z k |
0,95 |
В |
качестве |
|
начального |
|
приближения |
проще |
всего |
взять |
|||
x0 0, y0 |
0, |
z0 0 . Очевидно, |
что тогда при подстановке получим свободные |
||||||||
коэффициенты из новой системы: |
|
x1 1,1; y1 2,12; z1 |
0,95 . |
Подставив эти |
|||||||
числа, находим |
|
|
|
|
|
|
|
|
|
||
|
x2 |
0,2 2,12 |
0,3 |
0,95 |
1,1 |
0,961; |
|
|
|
||
а) |
y2 |
0,04 1,1 |
0,08 |
0,95 |
2,12 |
2; |
|
|
|
||
|
z2 |
0,15 1,1 |
0,1 2,12 |
0,95 |
0,997; |
|
|
|
|||
22

|
x3 |
0,2 2 |
0,3 |
|
0,997 |
1,1 |
0,999; |
|
|
|
|
|
|
|
|
|
||||||||
б) |
y3 |
0,04 0,961 |
0,08 |
|
|
0,997 |
2,12 |
2,002; |
|
|
|
|
|
|
||||||||||
|
z3 |
0,15 0,961 |
0,1 2 |
0,95 |
|
1,006; |
|
|
|
|
|
|
|
|
|
|||||||||
|
x4 |
0,2 2,002 |
|
0,3 |
|
1,006 |
1,1 |
1,001; |
|
|
|
|
|
|
|
|
||||||||
в) |
y4 |
0,04 0,999 0,08 |
|
1,006 |
2,12 |
2; |
|
|
|
|
|
|
|
|||||||||||
|
z4 |
0,15 0,999 |
|
0,1 2,002 |
0,95 |
|
|
1. |
|
|
|
|
|
|
|
|
|
|||||||
Заметив, |
что |
|
x4 |
x3 |
|
|
0,002 |
|
0,01, |
|
y4 |
y3 |
|
0,002 0,01 |
и |
|
z4 z3 |
|
0,006 0,01, |
|||||
|
|
|
|
|
|
|
|
|||||||||||||||||
вычисления |
прекращаем. |
|
Округляя |
по |
условию |
до |
|
сотых, |
получим |
|||||||||||||||
x 1, y |
2, z |
-1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Подставив в исходную систему, видим, что получаются тождества: |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
10 1 |
2 2 |
3 |
|
|
1 |
11, |
|
11 |
11, |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
1 |
|
25 2 |
2 |
1 |
53, |
|
53 |
53, |
|
|
|
|
|
||||
|
|
|
|
|
|
|
3 1 |
2 2 |
20 |
|
|
1 |
19. |
|
19 |
19. |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Ответ. |
x 1, |
y |
|
2, z |
|
|
1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Заметим, что приближённое решение совпадает с точным, поэтому погрешность вообще равна 0. Но, поскольку точное решение нам неизвестно, точность определяется сравнением двух последних приближений, а не последнего приближения с точным решением.
3.3. Вариант метода простых итераций
Иногда в системах (3.2) с квадратной матрицей А на главной диагонали aii 1
или aii |
1 , а вне диагонали другие aij |
0 . В этом случае, особенно при ручных |
|||||
вычислениях, может оказаться удобнее другой подход. |
|||||||
1. Умножим на (–1) те уравнения, где aii |
1 . Теперь все aii 1 или, что |
||||||
то же самое, aii |
1 i , где i |
0 . Очевидно, |
aii xi |
xi i xi . |
|||
2. |
Представим систему AX |
F как X |
A X |
B , где в матрице A' на глав- |
|||
ной диагонали aii |
i , а остальные элементы – такие же, как в A; |
||||||
3. |
Перенесём вправо: |
X |
A X |
F . Проще говоря, из всех уравнений |
|||
надо выразить xi |
через остальные x j и через |
i xi |
по обычным арифметическим |
||||
правилам переноса.
Система приведена к виду X = CX + D. Выбираем начальное приближение и решаем систему методом простых итераций.
23

Пример. Решим с точностью 0,01 систему
0,8x |
0,3 y |
1,9, |
0,1x |
0,9 y |
0,2. |
Решение. Условие (3.3) сходимости выполнено: 0,8 0,3; 0,9 0,1 . Коэффициенты на главной диагонали можно представить как 0,8 = 1–0,2 и –0,4 = 0,6– 1, тогда
|
|
|
|
x 0,2 x |
0,3 y |
1,9, |
||
|
|
|
|
0,1x 0,1y y |
|
0,2. |
||
Последняя система преобразуется к виду |
|
|
|
|||||
x |
0,2 x |
0,3 y |
1,9, |
x |
2x |
3 y |
19 /10, |
|
или |
|
|
|
|
||||
y |
0,1x |
0,1y |
0,2. |
y |
x |
y |
2 |
/10. |
Второй способ записи удобнее при вычислениях вручную или на калькуляторе. Выбираем x0 0, y0 0 , тогда
x1 |
0,2 0 |
0,3 0 |
1,9 |
1,9; |
|
|
||||
y1 |
0,1 0 |
0,1 0 |
0,2 |
0,2; |
|
|
||||
x2 |
0,2 1,9 |
0,3 0,2 |
1,9 |
2,22; |
||||||
y2 |
0,1 |
1,9 |
0,1 0,2 |
0,2 |
0,41; |
|||||
x3 |
0,2 |
2,22 |
0,3 0,41 |
1,9 |
2,22; |
|||||
y3 |
0,1 2,22 |
|
0,1 0,41 |
0,2 |
0,47; |
|||||
x4 |
0,2 2,22 |
0,3 0,47 |
1,9 |
2,18; |
||||||
y4 |
0,1 2,22 |
0,1 0,47 |
0,2 |
0,42, |
||||||
и так, пока не получим x8 x7 2,20 и y8 |
|
y7 |
0,47 – совпадение до сотых. |
|||||||
Ответ. Решение системы с точностью 0,01 таково: x = 2,2 и y = 0,47.
З а м е ч а н и е. Продолжив действия с большим числом знаков, можно увидеть, что x = 2,2 и y = 0,4(6) – точное решение системы.
Указанный вариант метода предпочтительнее (быстрее приводит к решению) в системах с большим числом неизвестных, когда коэффициенты на главной диагонали близки к 1, но меньше 1. Если же коэффициенты немного превышают 1, оба варианта метода простой итерации приводят к цели примерно за одно и то же число шагов.
Как отмечалось выше, условие (3.3) диагонального преобладания достаточно для сходимости, но некоторые системы решаются методом простых ите-
24

раций и без его выполнения (подобное имело место для нелинейных уравнений с одной переменной). Однако если метод простых итераций привел к решению, то заведомо выполнялось необходимое условие, а именно справедлива следующая теорема.
Теорема. Последовательность X k 1 CX k D сходится тогда и только тогда, когда все собственные числа матрицы C (возможно, комплексные) по модулю меньше 1. При этом последовательность сходится к решению системы $
X CX D .
Напомним, что собственные числа матрицы C – это решения уравнения
|
c11 |
c12 |
|
c1n |
|
|
det A E |
c21 |
c22 |
|
c2n |
0 |
|
|
|
|
|
|||
|
|
|||||
|
cn1 |
cn2 |
cnn |
|
||
относительно  .
.
При условии (3.3) собственные числа всегда меньше единицы и метод сходится. Однако меньше единицы они могут быть и без диагонального преобладания.
К сожалению, поиск собственных чисел в матрице выше 2-го порядка сложен и сам по себе является задачей, обычно решаемой только приближенно.
Путём элементарных преобразований любую систему можно превратить в систему с диагональным преобладанием, но универсальным алгоритмом такого превращения служит только метод Гаусса. Но это неэкономично и фактически заставляет решать систему более громоздким способом, чем метод простых итераций. Любые другие способы превращения системы в систему с диагональным преобладанием зависят от конкретного примера.
3.4. Метод Зейделя
По-прежнему мы решаем систему уравнений
a11x1 |
a12 x2 a1n xn |
f1, |
|
a21x1 |
a22 x2 |
a2n xn |
f 2, |
|
|
ann xn |
|
an1x1 |
an2 x2 |
f n, |
|
заменяя её на равносильную систему X |
CX D . |
||
25

Отличие метода Зейделя от метода простых итераций в том, что на каждом шаге учитываются уже новые значения переменных с меньшими номерами, то есть формулы пересчёта имеют вид
x1k 1 x2k 1
x3k 1
xnk 1
c |
x k |
c |
|
x k |
c |
|
x k |
|
|
|
|
||||
12 |
2 |
13 |
|
3 |
|
1n |
|
n, |
|
|
|
||||
c |
|
x k 1 |
c |
23 |
x k |
c |
2n |
x k |
|
||||||
|
21 1 |
|
|
|
3 |
|
|
|
n, |
(3.4) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c |
|
x k 1 |
c |
33 |
x k 1 |
c |
2n |
x k |
|
||||||
|
31 1 |
|
|
2 |
|
|
|
|
n, |
||||||
c |
|
x k 1 |
c |
|
n2 |
x k 1 |
c |
nn |
1 |
x k 1 |
|||||
|
n1 1 |
|
|
|
2 |
|
|
|
|
|
n 1. |
||||
В общем виде |
xik |
1 |
cij x kj |
1 |
cij x kj . |
Если формулы пересчёта получены |
||
|
|
|
|
j i |
|
|
j i |
|
2-м способом, |
то |
есть |
переменная |
содержит ссылку на саму себя, то |
||||
xik 1 |
cij x kj |
1 |
cij x kj . |
|
|
|
|
|
|
j i |
|
j i |
|
|
|
|
|
В методе простых итераций все переменные в правой части имели индекс k. Теперь же над уже пересчитанными переменными стоит индекс k 1.
Отличие условий сходимости двух методов выходит за рамки данного пособия. Можно считать, что оба метода сходятся для одних и тех же систем, что практически всегда и происходит.
Пример 1. Решим с точностью 0,001 систему
1,2 x |
0,2 y |
0,5; |
|
0,3x |
0,9 y |
1. |
|
Решение. Запишем систему в виде |
|
||
x |
0,2 x |
0,2 y |
0,5; |
y |
0,3x |
0,1y |
1. |
Условия, допускающие решение итерационными методами, выполнены:
1,2 |
0,2 |
и |
|
0,9 |
0,3 . |
Выбрав x0 |
0, y0 0 , |
подстановкой |
находим |
|
x1 |
0,2 |
0 |
0,2 |
0 |
0,5 |
0,5. |
|
|
|
|
Но, в отличие от метода простых итераций, значение y1 находим не как |
||||||||||
y1 |
0,3 0 |
0,1 0 |
1 1 , а, с учётом x1 |
0,5 , как y1 |
0,3 0,5 |
0,1 0 1 |
0,85. |
|||
В следующих приближениях каждое новое значение xk |
сразу же использу- |
|||||||||
ется при подсчёте yk , а не при подсчёте yk 1 . |
|
|
|
|||||||
Продолжим пересчёт с одной запасной цифрой, округляя результаты до четырёх знаков после запятой.
26

x2 |
0,2 0,5 |
0,2 0,85 |
0,5 |
0,57, |
|
|
|||||||
а) |
|
|
|
|
|
|
|
|
|
|
|
|
|
y2 |
0,3 0,57 |
0,1 0,85 |
|
1 |
0,914; |
|
|
||||||
x3 |
0,2 |
0,57 |
|
0,2 |
0,914 |
|
0,5 |
0,5688, |
|||||
б) |
|
|
|
|
|
|
|
|
|
|
|
|
|
y3 |
0,3 |
0,5688 |
0,1 |
0,914 |
|
1 |
0,9208; |
||||||
(достигнута точность 0,01) |
|
|
|
|
|
||||||||
x4 |
0,2 0,5688 |
0,2 0,9208 |
0,5 |
0,5714, |
|||||||||
в) |
|
|
|
|
|
|
|
|
|
|
|
|
|
y4 |
0,3 0,5714 |
0,1 0,9208 |
1 |
0,9216; |
|
||||||||
x5 |
0,2 0,5714 |
0,2 0,9216 |
0,5 |
0,5700, |
|||||||||
г) |
|
|
|
|
|
|
|
|
|
|
|
|
|
y5 |
0,3 0,5700 |
0,1 0,9216 |
1 |
0,9211; |
|
||||||||
x6 |
0,2 |
0,5700 |
0,2 |
0,9211 |
0,5 |
0,5702, |
|||||||
д) |
|
|
|
|
|
|
|
|
|
|
|
|
|
y6 |
0,3 |
0,5702 |
0,1 |
0,9211 |
1 |
0,9211. |
|||||||
|
Ответ. С точностью 0,001 решение системы – это x = 0,570 и y = 0,921. |
||||||||||||
|
Замечание. Точное решение x |
65/114 0,5701754 и y 35/ 38 0,9210526 |
|||||||||||
легко получить методом Крамера. Разумеется, системы 2-го порядка, в отличие от систем высокого порядка, быстрее и проще решать по точным формулам, чем итерационно. Здесь лишь демонстрируется идея решения.
Пример 2. Решим методом Зейделя с точностью 0,01 систему из пункта (3.3):
0,8x 0,3 y 1,9,
0,1x 0,9 y  0,2,
0,2,
также заменив её на равносильную систему
|
|
|
|
|
|
|
|
|
x |
0,2 x |
0,3 y |
1,9, |
|
|
|
|
|
|
|
|
|
y |
0,1x |
0,1y |
0,2. |
Выбираем x0 |
|
0, y0 |
0 : тогда |
|
|
|
||||||
x1 |
0,2 0 |
0,3 0 |
1,9 |
1,9, |
|
|
|
|
|
|||
а) |
|
|
|
|
|
|
|
|
|
|
|
|
y1 |
0,1 1,9 |
|
0,1 0 |
0,2 |
0,39; |
|
|
|
|
|||
x2 |
0,2 1,9 |
0,3 0,39 |
1,9 |
2,163, |
|
|
|
|||||
б) |
|
|
|
|
|
|
|
|
|
|
|
|
y2 |
0,1 2,163 |
0,1 0,39 |
0,2 |
0,455; |
|
|
|
|||||
x3 |
0,2 2,163 |
0,3 0,455 |
|
1,9 |
2,197, |
|
|
|
||||
в) |
|
|
|
|
|
|
|
|
|
|
|
|
y3 |
0,1 2,197 |
0,1 0,455 |
|
0,2 |
0,465; |
|
|
|
||||
27

x4 |
0,2 2,197 |
0,3 0,465 |
1,9 |
2,2, |
г) |
|
|
|
|
y4 0,1 2,2 0,1 0,465 0,2 0,467.
На следующем шаге значения (с точностью 0,001) не изменятся:
x5 0,2 2,2 0,3 0,467 1,9 2,2
д)
y5 0,1 2,2 0,1 0,467 0,2 0,467.
Ответ. С точностью 0,001 решение системы – числа x = 2,2 и y = 0,467. Видно, что метод Зейделя сходится быстрее, чем метод простых итераций.
Это особенно заметно в системах с большим числом уравнений и неизвестных. Пример 3. Решим систему уравнений
4 x |
2 y |
20 z |
1, |
15 x |
3 y |
3z |
9, |
2 x |
18 y |
6 z |
0. |
с тремя неизвестными x,y,z.
Переставим уравнения, чтобы максимальные коэффициенты оказались на главной диагонали:
15 x |
3 y |
3z |
9, |
2 x |
18 y |
6 z |
0, |
4 x |
2 y |
20 z |
1. |
Теперь можно разделить уравнения на 15, 18 и 20 соответственно, чтобы затем выразить переменные x, y, z. Однако при вычислениях "вручную" 2-е уравнение лучше разделить на 20 и выразить y сам через себя.
x |
0,2 y 0,2 z 0,6, |
|
0,1x |
0,9 y 0,3z 0, |
|
0,2 x 0,1y z 0,05. |
||
Последняя система очевидным образом преобразуется к виду |
||
x |
|
0,2 y 0,2 z 0,6, |
y |
|
0,1x 0,1y 0,3z, |
z |
|
0,2 x 0,1y 0,05. |
Выбираем x0 0, y0 0, z0 |
0 |
и проводим пересчёт по формулам (3.4) с |
записью индекса (номера) приближения внизу:
28

а)
б)
в)
г)
x1 |
0,2 0 |
0,2 0 |
0,6 |
0,6, |
|
|
|||
y1 |
0,1 |
0,6 |
|
0,1 0 |
0,3 0 |
0,06, |
|
|
|
z1 |
0,2 |
0,6 |
0,1 |
0,06 |
0,05 |
0,076; |
|||
x2 |
0,2 |
0,06 |
0,2 |
|
0,076 |
0,6 |
0,5728, |
||
y2  0,1 0,5728 0,1
0,1 0,5728 0,1 0,06
0,06 0,3
0,3 0,076
0,076 0,0861,
0,0861,
z2  0,2 0,5728 0,1
0,2 0,5728 0,1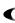 0,0861
0,0861 0,05
0,05 0,0732;
0,0732;
x3 |
0,2 |
0,0861 |
0,2 |
0,0732 |
0,6 |
0,5682, |
|
||
y3 |
0,1 |
0,5682 |
0,1 |
0,0861 |
0,3 |
0,0732 |
0,0874, |
||
z3 |
0,2 |
0,5682 |
0,1 |
0,0874 |
0,05 |
0,0723; |
|
||
x4 |
0,2 |
0,0874 |
0,2 |
0,0723 |
0,6 |
0,5680, |
|
||
y4  0,1 0,5680 0,1
0,1 0,5680 0,1 0,0874
0,0874 0,3
0,3 0,0723
0,0723 0,0872,
0,0872,
z4  0,2 0,5680 0,1
0,2 0,5680 0,1 0,0872
0,0872 0,05
0,05 0,0723.
0,0723.
Замечаем, что значения x4 , y4 по сравнению с x3 , y3 изменились только в 4-
м знаке, z4 совпало с z3 .
Ответ. С точностью 0,001 решение системы таково: x = 0,568, y = – 0,087, z = –0,072.
Разумеется, такое же решение получилось бы и при делении 2-го уравнения на 18, а при работе в EXCEL или при программировании метода
дробные коэффициенты не представляют трудностей. |
|
|
|
||||
3.5. Матричная запись метода Зейделя |
|
|
|
||||
Пусть система AX |
B любым способом приведена к виду X |
CX D . |
|||||
Разложим матрицу Cn n |
на сумму: |
|
|
|
|
|
|
|
Cn n |
U n n Vn n , |
|
|
|
|
|
При этом её элементы uij определяются так: |
uij |
cij для |
j i |
и uij |
0 для |
||
j i . В матрице V, наоборот, vij |
0 для j i и vij |
cij |
для j |
i . |
|
|
|
Тогда итерационная последовательность X k 1 |
UX k 1 |
VX k |
D . |
|
|||
Например, если получено уравнение, в матричном виде записываемое как
29

|
x |
0,3 |
|
0,2 |
0,1 |
x |
5 |
|
|
|
|
y |
0,04 |
0,05 |
0,2 |
y |
6 |
, |
|
|
|
|
z |
0,15 |
0,12 |
0,4 |
z |
7 |
|
|
|
|
то его можно представить так: |
|
|
|
|
|
|
|
|
|
|
x |
0 |
0 |
0 |
x |
0,3 |
|
0,2 |
0,1 |
x |
5 |
y |
0,04 |
0 |
0 |
y |
0 |
|
0,05 |
0,2 |
y |
6 . |
z |
0,15 |
0,12 |
0 |
z |
0 |
|
0 |
0,4 |
z |
7 |
Тогда решение по методу Зейделя равносильно решению матричного уравнения
xk 1 |
0 |
0 |
0 |
xk 1 |
0,3 |
0,2 |
0,1 |
xk |
5 |
y k 1 |
0,04 |
0 |
0 |
y k 1 |
0 |
0,05 |
0,2 |
y k |
6 |
z k 1 |
0,15 |
0,12 |
0 |
z k 1 |
0 |
0 |
0,4 |
z k |
7 |
относительно столбца xk 1; yk 1; zk 1 T , поскольку столбец xk ; yk ; zk T на данном шаге уже известен. Однако по построению никакого уравнения здесь нет, и все элементы этого столбца находятся простым вычислением, подобно тому, как находятся переменные при обратном ходе в методе Гаусса.
§ 4. Метод прогонки
4.1.Описание метода
Вприложениях встречаются разрежённые системы уравнений, ко-
гда большинство элементов матрицы равны нулю. Так, при численном решении дифференциальных уравнений, описывающих рынок спроса и предложения или производство с нелинейными издержками, в системе остаются только диагональные коэффициенты и по два коэффициента слева и справа. Такие же ситуации часты для уравнений в естественнонаучных дисциплинах. В этом случае весьма экономичен метод прогонки. При его применении число действий пропорционально числу уравнений (а не кубу, как в методе Гаусса). Решение получается за один шаг, а не в результате итераций, и точность зависит только от точности входных данных
иот округлений.
Вуказанных случаях коэффициент на диагонали всегда отличен от
нуля, каждое уравнение можно разделить на aii 0 и получить на диаго-
нали единицы. Поэтому в дальнейшем считаем, что эта операция уже выполнена и все aii 1. Итак, пусть дана система уравнений AX = F (в мат-
ричном виде):
30
