
5404
.pdf
предполагается постоянной, которая определяет "внутреннюю норму прибыли" сделки. Если, например, окажется, что при другом распределении капитала (то есть при другом виде уравнения (7.1) вели-
чина 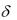 окажется больше, то необходимо выбрать второй способ вложения капитала).
окажется больше, то необходимо выбрать второй способ вложения капитала).
В уравнении (7.1) можно перейти от силы процента 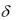 к процентной ставке в единицу времени по формуле
к процентной ставке в единицу времени по формуле 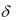 = ln(l + i):
= ln(l + i):
a (1 i) t j |
b (1 i) tj . |
(7.2) |
|
b |
|
n |
|
|
t j |
t j |
|
j 1 |
|
j 1 |
|
Уравнение стоимости в форме (7.2) называется уравнением доходности относительно i. В этом случае i называется внутренней доходностью в единицу времени.
Обозначим
Се |
bt |
j |
at |
. |
|
|
|
|
о |
|
|
j |
|
|
|
|
|
Тогда уравнения (7.1) и (7.2) примут вид: |
|
|||||||
|
|
|
|
n |
C e |
t j 0. |
(7.3) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
j |
|
|
|
|
|
|
j |
1 |
|
|
|
|
|
|
|
n |
|
|
i) t j 0. |
|
|
|
|
|
|
Ct j (1 |
(7.4) |
||
|
|
|
|
j |
1 |
|
|
|
Величина Ct j носит название чистого движения наличности на
момент tj.
До сих пор рассматривалась сделка, описываемая дискретными по-
токами наличности. Пусть имеется сделка, описываемая непрерывным потоком наличности, где 1(t) – норма доходов, 2(t) – норма расходов и
(t) = 1(t) – 2 (t) – чистая норма движения наличности. В этом случае уравнение стоимости будет иметь вид
(t)e t dt 0 . |
(7.5) |
|
|
0 |
|
62
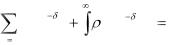
Для произвольной сделки, в которой присутствуют дискретные и непрерывные потоки наличности, уравнение стоимости имеет вид:
n |
|
|
t j |
|
|
(7.6) |
|
|
|
|
|
||
C |
|
e |
(t)e |
t |
dt 0. |
|
t |
|
|
||||
|
j |
|
|
|
|
|
j 1 |
|
|
|
0 |
|
|
Замечание. Уравнение (7.6) занимает центральное место в сфере фи-
нансово-экономических расчётов, так как описывает, в принципе, любую сделку. С этим уравнением связаны основные задачи финансовой ма-
тематики: (1) нахождение i по заданным отрицательным и положительным потокам наличности, (2) нахождение отрицательного потока по заданной норме прибыли и положительному потоку, (3) нахождение положительного потока по заданному отрицательному потоку и норме прибыли и т.д.
7.3. Условия существования корней уравнения стоимости
Если обратиться к уравнению (7.4), то формально оно имеет смысл при условии
1 + i > 0 или i> –1. |
(7.7) |
Условие (7.7) означает, что в уравнении (7.4) операции производятся над вещественными числами. Хотя значения i, удовлетворяющие
неравенству –1<i<0, и не имеют непосредственного экономического
смысла, будем рассматривать все значения, удовлетворяющие (7.7).
Рассмотрим варианты:
1. Уравнение (7.4) не имеет корней. В этом случае для данной сделки не существует 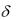 и, следовательно, не существует внутренней доходности i.
и, следовательно, не существует внутренней доходности i.
2. Уравнение (7.4) имеет более одного корня, причём положительных корней либо не существует, либо существует более одного. В этом случае говорят, что внутренняя норма прибыли и, следовательно, вну-
тренняя доходность для данной сделки также не существует.
63

3. Существует единственный корень уравнения (7.4). Тогда его
решение 0 носит название внутренней нормы прибыли, то есть доход-
ность сделки. ( i e 0 |
1 ). |
0 |
|
4. Существует единственный положительный корень 0 > 0 уравнения
(7.4) (могут существовать при этом и отрицательные корни). Тогда
также |
i e 0 |
1 0 носит название доходности. |
|
0 |
|
Таким образом, доходность сделки существует тогда и только тогда,
когда уравнение (7.4) имеет единственное решение относительно 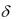 или единственное положительное решение.
или единственное положительное решение.
Сформулируем условия существования доходности сделки, в част-
ности условия существования положительной доходности.
Теорема 1. Пусть для сделки все расходы предшествуют всем доходам
(или наоборот), тогда существует единственное решение уравнения
доходности.
Теорема 2. Пусть сделка задана моментами времени t1<t2<…<tn и
чистыми движениями наличности Ct j , 1 j |
п. |
|
Пусть накопленные к |
|
m |
|
|
|
|
моменту времени tm итоговые суммы Аm = |
C |
t |
, |
1 ≤ m ≤ n, обладают |
|
|
j |
|
|
j |
1 |
|
|
|
следующими свойствами:
1) A1 0, An 0 ;
2) после исключения нулевых значений последовательность А1, А2,.,. Ап
содержит одну перемену знака. Тогда уравнение доходности имеет только один положительный корень.
Теореме 2 удовлетворяет сделка, в которой все расходы предше-
ствуют всем доходам и итоговая сумма поступлений превосходит
итоговые затраты.
Сделка вида { Ct j } = {–5,1, –3,8,4} также удовлетворяет теореме 2.
Действительно, А1 |
= –5; А2 |
= Ct |
Ct |
|
4 ; А3 |
= Ct |
Ct |
Ct |
7; |
|
|
1 |
|
2 |
|
1 |
2 |
3 |
|
64

А4 = Сt1 |
|
Ct2 Ct3 |
Ct4 |
|
1; А5 = Ct |
Ct |
2 |
Ct |
3 |
Ct |
4 |
Ct |
5. |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
5 |
|
|
|||||
|
Тогда последовательность {Ат} = {–5,–4,–7,1,5} содержит одну |
||||||||||||||||||||||||
перемену знака, причём A1 |
0, A5 |
0 . |
|
|
|
|
|
|
|
|
|||||||||||||||
|
Пример 7.1. Найти доходность в задаче А (пункт 7.1. Постановка |
||||||||||||||||||||||||
задачи). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Решение. Составим уравнение доходности. Для этого вначале опи- |
||||||||||||||||||||||||
шем |
|
|
поток |
чистого |
|
движения |
|
наличности |
в |
форме |
|||||||||||||||
Ct |
0 |
P, Ct |
wP, Ct |
wP, Ct |
n |
wP P . |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
1 |
|
|
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Тогда уравнение доходности примет вид |
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
P wP(1 i) 1 |
wP(1 i) 2 ... wP(1 |
i) |
n |
|
P(1 |
i) n |
0 . |
(7.8) |
||||||||||||
|
Пользуясь формулой суммы геометрической прогрессии, запишем |
||||||||||||||||||||||||
равенство (7.8) в виде |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
P wP |
(1 i) 1 |
|
(1 i) (n 1) |
P(1 i) n |
0 . |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Преобразуем последнее равенство к виду |
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
P 1 |
|
(1 i) n |
|
|
w |
P 1 |
|
(1 |
i) n |
|
|
0 . |
|
|
(7.9) |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
После сокращения в (7.9) на величину: P 1 |
|
(1 i) n , получим равенство |
|||||||||||||||||||||||
|
1 |
|
w |
0, то есть w = i. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Таким образом, внутренняя доходность в данной сделке равна w, что соответствует интуитивным представлениям, о доходности.
Пример 7.2. Инвестор вкладывает 500 у.д.е. в данный момент и 200
у.д.е. через два года и получает 1 000 у.д.е. через 5 лет. Найти доходность сделки.
Решение. По теореме 1 существует единственное решение уравнения доходности. Далее
65

Ct |
0 |
500 , Сt |
2 |
200 , Ct |
2 |
1 000 , |
A(0) |
500, A(1) |
700, |
A(2) 300. |
|||
Последовательность А(0), A(1), А(2) имеет одну перемену знака,
следовательно, по теореме 2 решение уравнения доходности положительно.
Уравнение доходности имеет вид f(i) = –500 – 200(1 + i)-2 + 1 000(1 + i)-5 = 0.
Так как f(0) = –500 – 200 +100 = 700 > 0, а f(1) = –500 – 200 × |
1 |
1000 |
1 |
< |
|
4 |
32 |
||||
|
|
|
0, то корень i0 лежит между числами 0 и 1. С помощью метода деления отрезка пополам с точностью, например, до 0, 001 находим, что i0 = 0,083,
или 8,3%.
Доходность в данной задаче имеет следующую простую интерпре-
тацию: если инвестор вложит в банк в данный момент 500 у.д.е. и через
2 года сумму 200 у.д.е. под i процентов годовых, то при i < 0,083 через 5
лет он получит менее 1 000 у.д.е., а при i > 0,083 – более 1 000 у.д.е.
Действительно, уравнение, используемое при вычислении внутренней доходности i0, можно представить в форме равенства
500 (1+ i)5 + 200 (1+i)3 = 1 000. |
(7.10) |
Накопление капитала 500 у.д.е. за 5 лет по процентной ставке I составит величину
S1= 500(1+i)5 в схеме сложных процентов. Капитал 200 у.д.е. за 3 года даёт наращение S2 = 200(1+i)3. Таким образом, накопление совокупного капитала S1 + S2 составляет левую часть уравнения (7.10).При i = i0
уравнение (7.10) превращается в тождество, так как внутренняя доходность i0 является корнем уравнения стоимости. Так как левая часть уравнения (7.10) монотонно возрастает по мере возрастания процентной ставки i, то при i > i0 накопленный капитал S1 + S2 будет больше суммы
1 000 у.д.е., а при i < i0 величина S1 + S2 будет меньше 1 000 у.д.е.
66
Из решения примера 7.2 следует, что внутренняя доходность является инструментом сравнения финансово – экономических операций (сделок).
Так, например, при i > i0 доход от вложения средств в банк будет выше,
чем доход от предпринимательской деятельности. При i < i0 доход от предпринимательской деятельности будет выше, чем от вложений в банк.
Отметим, что процентная ставка i является внутренней доходностью операции вложений в банк, если сумму 1 000 у.д.е. заменить величиной S = S1 + S2 .
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ
1.Какова цель введения внутренней нормы прибыли?
2.Какой вид имеет уравнение стоимости?
3.При каких достаточных условиях существует внутренняя норма прибыли?
67
8.Задачи для самостоятельной работы
1.Найти сумму простых процентов по кредиту 1 000 у.д.е на 53 дня при а) 8 % в год; б) 3 % в месяц. В случае а) найти годовую учётную ставку.
2.Кредит 135 у.д.е. погашается суммой 180 у.д.е. за 67 дней. Найти простую квартальную процентную ставку и годовую учётную ставку.
3.Найти текущую стоимость суммы 750 у.д.е., уплачиваемой через 5
лет при простой процентной ставке 2% в квартал. Найти соответствующую годовую учётную ставку.
4. Дисконтировать 150 у.д.е. на 5 месяцев при простой учётной ставке d = 0,06 в год. Найти годовую процентную ставку.
5. Суммы 100 и 250 у.д.е. требуются соответственно через 3 и 5 лет.
Предполагая годовую процентную ставку равной 10 %, найти инвестируемую сумму, формирующую накопление по формуле простых процентов.
6. Инвестируемая сумма 100 у.д.е. позволяет при начислении по простому годовому проценту i выплачивать через 3 месяца 40 у.д.е. и
затем ещё через 6 месяцев 119 у.д.е. Найти i в процентах.
7. Дана учётная ставка 8 % в год. Найти соответствующую ей простую процентную ставку и накопление капитала 1 500 у.д.е. за 35 дней.
8.Срочная ценная бумага сроком на 72 дня под 15 % годовых с номинальной стоимостью 1 000 у.д.е. продаётся через 25 дней банку с учётной ставкой 17 % годовых. Найти цену продажи.
9.Инвестируемая сумма 125 у.д.е. позволяет под 22 % годовых подучить через 4 месяца 50 у.д.е. и затем ещё через 7 месяцев X у.д.е.
Найти X.
10. Инвестируемая сумма 625 у.д.е. позволяет под 25 % годовых получить через 2
месяца X у.д.е. и затем ещё через 10 месяцев – 700 у.д.е. Найти X.
11. Вексель с номинальной стоимостью 100 x + 400 у.д.е. с процентной
68
ставкой (0,1 у +12) % годовых сроком на Z + 70 дней продаётся через 40 – z дней после подписания векселя банку с учётной ставкой (10-0,1 у) %
годовых. Найти норму прибыли продавца и банка, если x – номер варианта, y – пятая цифра, z – четвёртая цифра зачётной книжки.
Решить следующие задачи на сложные проценты.
12. Фактическая процентная ставка на настоящее время составляет
28% в год, но через 2 года она понизится до 20 %. Найти накопление 1 500
у.д.е. за 5 лет.
13.По первоначальному вкладу 750 у.д.е. за 7 дет накоплена сумма 1 000 у.д.е. Найти фактическую годовую процентную ставку.
14.За три года накоплена сумма 7 500 у.д.е. при фактической процентной ставке 9 % в год. Найти первоначальный вклад.
15.Даны две номинальные процентные ставки 11,5 % в год сроком на
7 дней и 11,375 % сроком на 14 дней. Найти накопление 1 000 000 у.д.е. за два последовательных недельных срока и на один двухнедельный срок.
16. Найти накопление суммы 750 у.д.е. за 5 лет, если коэффициент накопления имеет вид:
А (t1, t2) = e0,05 (t2 – t1).
Проверить выполнение принципа согласованности.
17. Фактическая процентная ставка на настоящее время составляет
17% в год, но через три года она повысится до 22 % в год. Найти накопление 2 500 у.д.е. за 7 лет.
18. По первоначальному вкладу 250 у.д.е. за 8 лет накоплена сумма
525 у.д.е. Найти фактическую годовую процентную ставку.
19. Найти текущую стоимость накопленной за 10 лет суммы 1 500
у.д.е. при годовой процентной ставке 15 %.
20. Номинальная процентная ставка X % в год сроком на 1 день сумму
100 000 у.д.е. при двукратном применении увеличивает до 1000 25 у.д.е.
Найти X.
69

21. Найти текущую стоимость суммы 3 000 у.д.е. за 5 лет, если
коэффициент накопления имеет вид:
A (t1 , t2) = е0,05 (t1– t2).
Проверить выполнение принципа согласованности.
Решить следующие задачи, используя понятие силы процента.
22. Найти |
накопленную стоимость суммы 250 у.д.е. за 75 дней, |
|
начиная от t = 0 |
при силе процента 1 (2 |
t) в год. |
23. При постоянной силе процента |
= 0,07 в год найти |
|
соответствующие ей годовую процентную и учётную ставки, а также на-
копление 100 у.д.е. за 10 месяцев.
24. Дана годовая процентная ставка i = 0,09. Найти эквивалентную ей силу процента, а также процентные ставки, конвертируемые один раз в 30
дней и в полгода. |
|
25. Сумма 350 у.д.е. инвестируется при силе процента |
at в год. |
Накопленная стоимость за 4 года, начиная от момента t = 2, равна 500
у.д.е. Найти .
26. Пусть время измеряется в годах и сила процента определяется формулой  0,1t. . Найти эквивалентную ей номинальную процентную ставку на срок 5 дней от момента t = 2 и накопление 100 у.д.е. за то же время.
0,1t. . Найти эквивалентную ей номинальную процентную ставку на срок 5 дней от момента t = 2 и накопление 100 у.д.е. за то же время.
27. Пусть сила процента определяется формулой Студли с па-
раметрами р = 0,12; r = 0,5; s = 0,07. Найти текущую стоимость 150 у.д.е. за
5 лет на момент t = 0. |
|
28. При силе процента |
1 (1 t) в год найти текущую стоимость |
на 1 марта 1989 года суммы 750 у.д.е., выплачиваемой 1 октября 1991 года,
если момент времени t 0 соответствует 1 сентября 1988 года. 29. При кусочно-постоянной силе процента
70
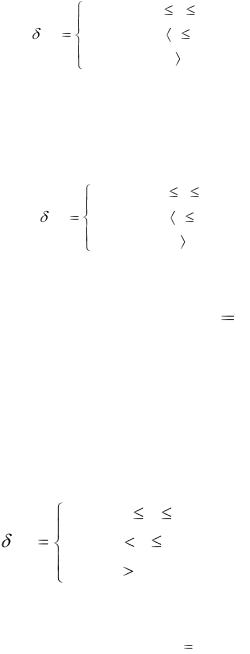
|
0,27, |
0 t |
2, |
(t) |
0,2, |
2 t |
3, |
|
0,15, |
t |
3. |
в год. Найти номинальную процентную ставку в год от момента времени t
==0 на срок 3 месяца.
30.Пусть сила процента в год даётся формулой
|
0,12, |
0 |
t 3, |
(t) |
0,8, |
3 t |
5, |
|
0,4, |
t |
5. |
Какая сумма даёт за 6 лет накопленную стоимость 300 у.д.е.?
31. Дана постоянная сила процента 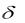 0,21в год. Найти эквивалентные ей годовую учётную ставку и годовые процентные ставки,
0,21в год. Найти эквивалентные ей годовую учётную ставку и годовые процентные ставки,
конвертируемые раз в день и в квартал.
Решить следующие задачи на тему: "Потоки наличности" 32. Пусть сила процента в год определяется формулой
|
0,12, |
0 |
t |
3, |
(t) |
0,8, |
3 |
t |
5, |
|
0, 4, |
t |
5. |
|
Найти дисконтирующий множитель V(t) затем текущую стоимость непрерывного потока наличности с нормой 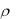 1 в год за 8 лет, начиная с момента t = 0.
1 в год за 8 лет, начиная с момента t = 0.
33. Бизнесмен должен уплатить 1 000 у.д.е. 1 января 1986 года, 3 500
у.д.е 1 января 1987 года и 3 000 у.д.е. 1 июля 1987 года. Полагая силу процента постоянной и равной 0,04 в год, найти стоимость этих платежей на 1 января 1984 года и пересчитать на 1 марта 1986 года.
34. Найти цену ежегодной ренты, выплачиваемой в конце каждого года в течение 10 лет с ежегодной суммой 150 у.д.е. , если процентная ставка равна 12 %.
71
