5404

мы называем Р текущей или дисконтированной стоимостью капитала А, и

А – накопленной стоимостью капитала Р. В данном примере

d = 1300 1000 = 0, 077,

3 1300

то есть годовая учётная ставка равна 7, 7 %.

Найдём соотношение между учётной и процентной ставками. Из формулы (1.8) следует:

Экономический смысл равенства (1.10) состоит в том, что учётную ставку можно рассматривать как текущую стоимость процентной ставки,

то есть дисконт – это процент, уплачиваемый вперёд.

Пример 1.6. Дисконтировать 900 у.д.е. за 7 месяцев при простой про-

центной ставке 10 % в год.

Решение. Найдём текущую стоимость суммы 900 у.д.е.:

Пример 1.7. Дисконтировать 600 у.д.е. за 4 месяца при учётной ставке

9% в год. Найти процентную ставку.

12

то есть годовая процентная ставка равна 9,3 %.

Примером применения простых процентов служат долговые обя-

зательства, то есть письменные обязательства уплатить указанную сумму в указанный срок.

Пример 1.8 Обязательство

Москва Обязуюсь уплатить через шестьдесят дней после указанной даты по

распоряжению г-на А 2 000 у.д.е. с процентами по ставке 11 % в год.

Подпись Г-н В

Пусть это обязательство продаётся до срока платежа 2 октября 1987 г. и

дисконтируется по учетной ставке 9,5% в год. Определить:

1)цену продажи;

2)норму прибыли г-на А;

3)норму прибыли банка;

4)дату продажи с оптимальной нормой прибыли г-на А;

5)дату покупки с оптимальной нормой прибыли банка.

Решение. При сроке погашения обязательства t = 60 дней от времени продажи до срока платежа 31 октября остается t1 = 29 дней.

Номинальная стоимость Р0 = 2000 у.д.е., процентная ставка i = 0,11,

1. Для того чтобы найти цену продажи, необходимо фактическую стоимость дисконтировать на 29 дней с учётной ставкой 9,5 %:

2. Норма прибыли г-на А:

13

Из последней формулы следует, что CA(x) изменяется монотонно при

Следовательно,

14

Вывод: ценную бумагу в данном случае выгоднее продать сразу после заключения сделки, так как норма прибыли к концу срока уменьшается в 8

раз.

2. Пусть i – d – 365idt = 0 .

Вэтом случае СА(х) постоянна: СА (х) = d(1+ 365it ) . 3. Пусть i –d – 365idt = 0.

Вэтом случае СA(X) возрастает: max C(x) = CA (t), min CA(x) = =CA(1).

5. Исследуем норму прибыли банка:

Вывод: норма прибыли банка практически не зависит от времени

покупки.

ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ

1.Как вычисляются процентные деньги в схеме простых процентов?

2.Как определяются операции наращения и дисконтирования в схеме

3.Как определяется учётная ставка и в чём заключается её экономический смысл?

4.Какие соотношения связывают учётную и процентную ставки?

15

2.СЛОЖНЫЕ ПРОЦЕНТЫ

2.1.Понятие сложных процентов.

2.2.Номинальные процентные ставки.

2.3.Коэффициенты накопления.

2.1.Понятие сложных процентов

Простые проценты имеют ограниченное практическое применение.

Пусть по некоторому типу сберегательного счёта выплачиваются простые проценты по ставке i в год. Предположим, что эти проценты гарантируются в течение двух лет, а счёт можно закрыть в любое время.

Пусть вкладчик открывает в некоторый момент счёт с начальным вкладом Р, через год закрывает его и по формуле простых процентов получает сумму А = P(1 + i). Затем открывает новый счёт с суммой А, которая через год даёт сумму А1 = Р (1 + i)2 = Р (1 + 2i + i2) .

С другой стороны, если вкладчик не закрывает счёт два года, то он накопит капитал А = Р (1 + 2i). Капитал А1 больше капитала А на сумму Рi2

= (Рi)i. Эта величина представляет собой проценты, начисленные в конце второго года на проценты полученные в конце первого года.

Спрактической точки зрения трудно представить частые переводы денег

содного счёта на другой. Кроме того, в этом случае банк будет иметь дополнительные административные расходы и, что самое главное,

вкладчик, закрыв счёт, может не открыть новый, вложив деньги в другое предприятие. По этим соображениям банки сами начисляют проценты на проценты, по крайней мере, на срок более года, то есть переходят к сложным процентам.

Процедуру взятия сложных процентов можно описать следующим образом. Пусть вкладчик положил на счёт сумму Р под сложные проценты по ставке i в год. Обозначим через Ап сумму, которую он получит через п

16

лет. По определению, сумма, которую он получит в конце n + 1-го года, состоит из суммы Ап плюс проценты от этой суммы за год, то есть: А(n+1) =An

Так как А1 = Р (1 + i), из этого следует равенство

An = P(1 + i)n . (2.2)

Таким образом, формула (2.2) даёт накопление капитала при сложных процентах за n лет. Сумма сложных процентов как разность между накопленным капиталом и исходным за n лет находится по формуле

(2.1)

Отметим, что в формулах (2.2) и (2.3) n – целое положительное. В

дальнейшем мы будем рассматривать случаи, когда n – любое положи-

тельное число.

Пусть процентная ставка зависит от времени I = i(t) и постоянна в единичном интервале времени от t до t+1. Тогда формула накопления капитала будет иметь вид:

Формула (2.2) есть частный случай формулы (2.4), когда i постоянна. В

круг задач финансовой математики входят:

1. Вычисление процентной ставки как функции времени при задан-

ных начальном капитале, накопленной стоимости и алгоритме накопления.

2.Вычисление начального капитала по заданным Ап и i(t).

3.Вычисление Ап по известным i(t) и Р.

2.2. Номинальные процентные ставки

Перейдём к изучению ситуации, когда накопление происходит в про-

извольные интервалы времени (не обязательно целые). В качестве единичного интервала возьмём год, хотя можно рассмотреть и другие единицы. Рассмотрим сделку, заключаемую в момент времени t на срок h,

где h – любое (не обязательно целое) положительное число.

17

Определение. Номинальной процентной ставкой ih(i) в единицу времени за период от t до t + h называется такое число, что фактическая (простая)

процентная ставка за этот период равна h 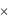in (t). Таким образом, если в момент времени t инвестируется капитал Р, то накопление капитала за период h находится по формуле

процентная ставка, выплачиваемая (или конвертируемая р-кратно). Опять

же i(1) = i

Пример 2.1. – Заданы номинальные годовые процентные ставки

Найти накопление капитала 1 000 у.д.е. за а) 2 дня, б) 1 неделю, в) 1

месяц.

Решение. Составим таблицу

Сроки

18

Замечание:

1.Номинальные процентные ставки примера 2.1 взяты из реальной практики деловой жизни Великобритании.

2.Если подсчитать доход от вложения 1 000 000 у.д.е. за два последовательных однодневных срока, то получим А = 1 000 000 (1 +

1/365 • 0,1175)2 = 1 000 644 (у.д.е.).

Прибыль за один двухдневный срок равна А = 1 000 000 (1 + 1/365 •

0,11625)2 = 1 000 637 (у.д.е.).

Это противоречие частично объясняется тем, что ожидается изменение процентных ставок и банки введением таких правил застраховывают себя от возможных потерь.

Если сумма 1 инвестируется на единичный срок при фактической процентной ставке hih(i), то сумма процентов за этот срок равна

вложенную единичную сумму можно конвертировать р раз и получить сумму процентов по формуле, аналогичной (2.3).

2.3 Коэффициенты накопления

Выберем некоторую фиксированную единицу времени (например, год).

Для t1<t2 под величиной A(t1,t2) будем понимать накопленную стоимость

19

единичной суммы за время t2 – t1. Из определения ih(t) следует, что

Отсюда получаем формулу для номинальной процентной ставки:

Равенство (2.10) соответствует тому практически очевидному факту, что за промежуток времени нулевой длины накопления капитала не происходит. Величину A(t1,t2) часто называют коэффициентом накопления,

так как величина накопления за время t2 – t1 начального капитала Р

Рассмотрим теперь три момента времени t0<t1<t2. Тогда накопление единичного капитала за время t2 – t0 определяется коэффициентом накопления A(t 0 ,t2). С другой стороны, накопление единичного капитала можно разбить на два этапа. За время t1 – t0 накопление определится коэффициентом A(t0,t1), а за время t2 – t1 величину накопленного капитала определим по формуле (2.11) как величину A(t0,t1)A(t1,t2). При нормально

Равенство (2.12) носит название принципа согласованности. На практике принцип согласованности, как правило, носит приближённый характер,

ввиду административных расходов, правил налогообложения и т.д. Тем не менее нужно иметь в виду, что в некоторых математических моделях появляются функции A(t1, t2), которые не удовлетворяют равенству (2.12).

Пример 2.2. Найти накопленную стоимость суммы 100 у.д.е.:

20

а) при номинальной ставке 4% в год на срок 1 квартал,

б) при номинальной ставке 6% в год на срок 1 месяц.

Решение:

А = 100 1,005 = 100,5 (у.д.е.).

Пример 2.3. Известно, что коэффициент накопления имеет вид (единица

времени –1 год) A(t1,tz) =exp 0,03(t2-t1).

а) показать, что A(t1,t2) удовлетворяет принципу согласованности;

б) найти накопление 1000 у.д.е. за 20 лет.

Перемножим (2.13) на (2.14) и воспользуемся свойством показательной

ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ

1.В чём принципиальное отличие простых процентов от сложных?

2.Как определяются операции наращения и дисконтирования в схеме сложных процентов?

21