
5404
.pdf
3.В чём отличие простой процентной ставки от номинальной?
4.Как определяется принцип согласованности?
3.СИЛА ПРОЦЕНТА
3.1.Определение силы процента.
3.2.Связь между силой процента и коэффициентом накопления.
3.3.Связь между номинальными процентными ставками и силой процента.
3.4.Текущая стоимость.
3.5.Формула Студли для силы процента.
3.1.Определение силы процента
В предыдущих разделах было введено понятие номинальной процентной ставки ih(t). Особый интерес представляет предел этого выражения при h 0 Знак "плюс" здесь означает тот факт, что h стремится к нулю справа,
то есть является положительной величиной. Этот предел называется силой процента, которую будем обозначать символом (t ).Таким образом, по определению,
|
h |
|
(3.1) |
(t) lim i |
|
(t). |
|
h0
Вфинансовом смысле силу процента можно рассматривать как номи-
нальную процентную ставку, конвертируемую мгновенно, однако на практике невозможно реализовать процентную ставку, конвертируемую сколько угодно часто в единицу времени. Поэтому хорошим приближением к силе процента, достаточным для целей практического финансового анализа, можно считать номинальную процентную ставку сроком на один день.
22

3.2 Связь между силой процента и коэффициентом накопления
Подставим в формулу (3.1) выражение для номинальной процентной ставки, при этом получим
(t) lim |
A(t, t h) 1 |
(3.2) |
|
|
|
|
|
h 0 |
h |
|
Коэффициент А(t,t+h) представляет собой накопление единичного капитала к моменту t + h, инвестированного в момент времени t. Таким образом, сила процента есть скорость изменения единичного капитала в момент времени t.
Поставим обратную задачу: найти коэффициенты накопления с помощью силы процента. Если эта задача будет решена, то сила процента будет той универсальной величиной, с помощью которой можно будет решать любые финансово-экономические вопросы.
Теорема. Если (t) непрерывна, a A(t0 ,t) имеет производную при t > to, где to – начальный момент времени, то при условии выполнения принципа согласованности имеет место формула
t |
|
|
|
A(t0,t) = exp (t)dt . |
(3.3) |
||
t0 |
|
|
|
Доказательство. Рассмотрим выражение w(t) = |
A(t, t |
h) 1 |
|
|
h |
|
|
|
|
||
и умножим числитель и знаменатель на величину A(to,t). Тогда на основании принципа согласованности получим
w(t) = |
A(t |
0,t) A(t,t h) A(t0,t) |
|
A(t0 |
,t h) A(t0,t) |
. |
(3.4) |
|
|
hA(t0 ,t) |
|
|
hA(t |
0,t) |
|||
|
|
|
|
|
|
|||
Так как величина A(to,t) не зависит от приращения h, то формула (3.1) в
силу (2.9) принимает вид
(t) |
1 |
lim |
A(t0 , t) |
A(t0 , t) |
. |
(3.5) |
|
|
|
||||
|
|
|
|
|
|
|
|
A(t0,t) h 0 |
h |
|
|||
Функция A(t0,t) является функцией одной переменной, а предел, стоящий в правой части (3.5), есть, по определению, производная от A(to,t). Поэтому
23
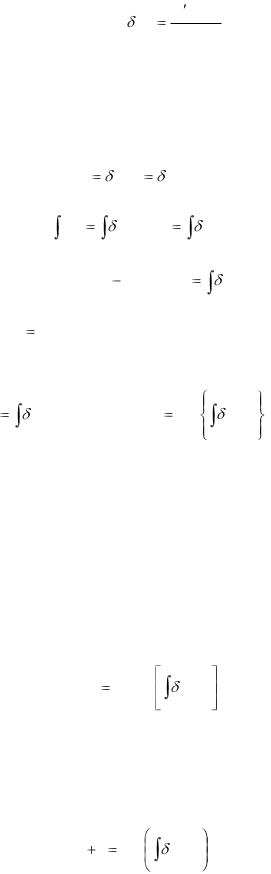
равенство (3.5) можно записать в виде
|
A (t0 , t) |
(3.6) |
(t) |
A(t0 , t) . |
Равенство (3.6) является дифференциальным уравнением первого порядка с разделяющимися переменными относительно неизвестной функции А. Решим (3.6):
|
|
1 dA |
|
, |
dA |
dt. |
(3.7) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
A dt |
|
A |
|
||||||||||
|
|
1 dA |
t |
dt, InA |
|
t |
t |
dt, |
|||||||
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
A |
|
|
|
|
|
|
t |
0 |
|
|||
|
t0 |
t0 |
|
|
|
|
|
|
t0 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
InA(t0 ,t) |
|
InA(t0 ,t0 ) |
dt. |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t0 |
Так как А(t0 , t0 ) |
1 (см. формулу (2.10)), то равенство (3.7) принимает |
||||||||||||||
вид |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
InA(t0 ,t) |
(t)dt или |
A(t0 , t) |
|
exp |
(t)dt . |
||||||||||
t0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t0 |
Теорема доказана.
Замечание. Доказательство этой теоремы имеет важное методоло-
гическое значение, так как здесь явно прослеживается основная идея теории сложных процессов – идея непрерывного роста денег. Если в начальный момент времени t = 0 инвестируется сумма Р 0 , то накопленный капитал A(t) за время t находится по формуле
|
t |
(3.8) |
|
|
|
A(t) P0 exp |
|
(t)dt . |
|
0 |
|
Из формулы (3.3) можно получить связь между силой процента и годовой процентной ставкой. Для этого достаточно в (3.3) положить t0 =
0, t = 1:
|
1 |
(3.9) |
1 1 exp |
|
(t)dt . |
|
0 |
|
24

Пример 3.1. Найти накопленную стоимость 100 у.д.е. за год при силе процента 0,083 5 в год. Найти годовую фактическую процентную ставку,
соответствующую этой силе процента.
Решение. По формуле (3.8)
1
A 1 100exp 0,0835dt .
0
1
По формуле Ньютона-Лейбница 0,0835dt 0,835, поэтому А (1) = 100е0,0835
0
у.д.е.
На основании формулы (3.9) i = е0,0835 – 1= 0,0871.
Пример 3.2. Годовая фактическая процентная ставка равна 6 % Найти соответствующую ей постоянную силу процента.
Решение. По формуле (3.9)
|
|
1 |
i |
e . |
|
(3.10) |
|
Тогда |
|
|
|
|
|
|
|
|
In(1,06) |
0,058. |
|
(3.11) |
|||
Пример 3.3. Накопление происходит при переменной силе процента, |
|||||||
которая задаётся формулой |
(t) |
a b exp(t /10), где единица измерения |
|||||
времени – год. Найти а, b, если известно, что сумма 100 у.д.е. даёт |
|
||||||
накопление 150 у.д.е. через 5 лет и 190 у.д.е. через 10 лет. |
|
||||||
Решение. Воспользуемся формулой (3.8) |
|
|
|||||
|
5 |
|
|
|
|
(3.12) |
|
А(5) |
100exp |
a |
b exp(t /10 dt |
150, |
|||
|
|||||||
|
0 |
|
|
|
|
|
|
|
10 |
|
|
|
|
||
A(10) |
100exp |
a |
b exp t /10 dt |
190. |
(3.13) |
||
|
|
0 |
|
|
|
|
|
Вычислим интегралы, стоящие в правых частях равенств (3.12), (3.13):
25
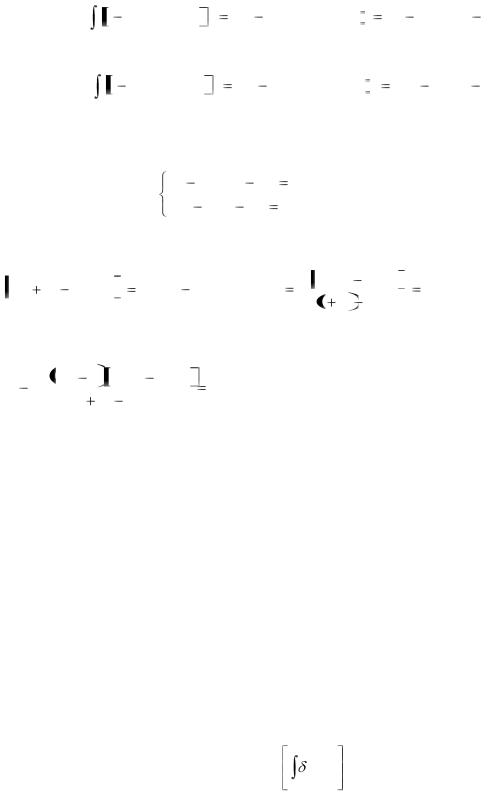
5 |
|
|
|
|
|
|
|
|
|
|
|
|
a |
b exp(t /10) dt |
(at |
10b exp(t /10) |
t 5 |
5a |
10b(e |
1/ 2 |
1), |
||||
t 0 |
|
|||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
a |
b exp(t /10) dt |
(at |
10b exp(t /10) |
t |
10 |
10a 10b(e |
1). |
|||||
t |
0 |
|||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
После этого система (3.12), (3.13) примет вид: |
|
|
|
|
|
|||||||
|
5a 10(e1/ 2 1)b |
In1,5, |
|
|
|
|
(3.14) |
|||||
|
10a 10(e 1)b |
In1,9. |
|
|
|
|
|
|||||
Умножим первое уравнение на 2 и вычтем из него второе: |
|
|||||||||||
10(1 e) 20e1/ 2 b |
2In15, In1,9 или |
b |
|
2In1,5 In1,9 |
0,0402 . |
|
||||||
10 1 e 20e1 / 2 |
|
|||||||||||
|
|
|
|
|
|
|
||||||
Подставим теперь выражение для в первое уравнение системы (3.14):
5a |
10 e1/ 2 |
1 2In1,5 In1,9 |
In1,5, |
а = 0,5448. |
|
10(1 |
е) 20е1/ 2 |
||||
|
|
|
3.3 Связь между номинальными процентными ставками и силой
процента
В предыдущем разделе была установлена связь между фактической годовой процентной ставкой и силой процента. Аналогичным образом можно получить соотношения, связывающие номинальные процентные ставки с силой процента и, следовательно, с фактической годовой про-
центной ставкой.
За период времени h от начального момента t0 = 0 единичный капитал
прирастится на величину A(0,h) = exp (t)dt .
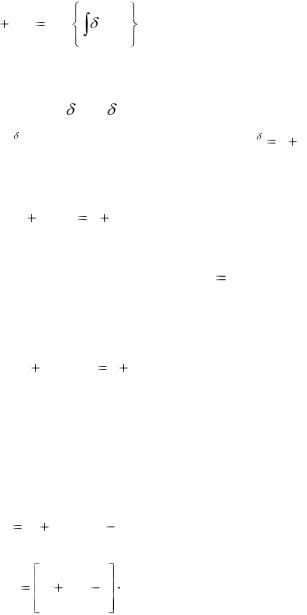
|
h |
(3.15) |
|
|
|
1 hih exp |
|
(t)dt . |
|
0 |
|
Рассмотрим практически важный случай, когда сила процента не зависит от времени, то есть (t)= . В этом случае формула (3.15)
принимает вид: 1+hih = e h |
Учитывая тот факт, что e 1 i (см.формулу |
||||||||||||
(3.10)) получим, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
(3.16) |
|
|
|
|
|
|
|
|
|
|
|
|
|||
(1 |
hi |
) h |
|
1 |
i. |
|
|
||||||
|
|
h |
|
|
|
|
|
|
|
|
|
||
Рассмотрим практически важный случай, когда h |
1 |
p-целое. Тогда |
|||||||||||
p |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
формула (3.16) примет вид |
|
|
|
|
|
|
|
|
|
|
|
|
|
(1 |
|
1 |
|
i |
( p) |
) |
p |
1 i. |
|
(3.17) |
|||
|
p |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|||
Здесь i(р) – номинальная процентная ставка, конвертируемая р раз в единицу времени, в частности в год. Из (3.17) можно получить
выражение i через i(р) и наоборот: |
|
|
|
|
|||||||
i |
(1 |
1 |
i |
( p) |
) |
p |
1, |
(3.18) |
|||
|
p |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
(3.19) |
|
|
|
|
|
|
|
|
|
|
|
||
i ( p) |
|
|
|
|
|
|
|
|
|||
|
(1 i) p |
|
|
1 p. |
|
||||||
Из формулы (3.19) следует, что номинальная процентная ставка i(р)
эквивалента фактической процентной ставке в единицу времени i в том смысле, что они приносят одинаковый доход за единицу времени.
Пример 3.4. Найти накопленную стоимость 100 у.д.е. за 20 лет при:
а) фактическая процентная ставка 5 % в год ;
б) номинальная процентная ставка 5 % в год, выплачиваемая ежеквартально;
27

в) фактическая ставка 5 % в год, выплачиваемая в течение 10 лет, и
номинальная процентная ставка, выплачиваемая ежеквартально в течение последующих 10 лет.
Решение. А. Пользуясь формулой (2.2), получим А = 100(1+0,05)20 =
=265,33 у.д.е.
Б. Так как 20 лет состоят из 80 кварталов, то А = 100(1 + 14  0,05)80 = 270,15
0,05)80 = 270,15
у.д.е.; |
|
|
|
|
В. А = 100(1 + 0,05)10 (1 |
1 |
0,05)40 |
267,73 у.д.е. |
|
4 |
||||
|
|
|
Пример 3.5. Пусть фактическая процентная ставка в год равна
10 %. Найти эквивалентную ей фактическую ставку в квартал.
Решение. Воспользуемся формулой (3.19): 14 i(4) (1 0,1)1/ 4 1 0,024.
Это фактическая квартальная ставка. Номинальная ставка: i(4) =
4 (1 0,1)1/ 4 1 0,096 .
0,096 .
Пример 3.6. При i = 0,07 найти: а) i(12), б) i(4), г) .
Решение. Воспользуемся формулой (3.19):
а) i (12) 12 (1 0,07)1/ 12 1 0,06785 ,
0,06785 ,
б) i (4)
в) i (2)
По формуле (3.10) 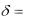
В этом примере выполняются неравенства: < i(12) < i(4) < i(2) < i.
Эти неравенства выполняются всегда, то есть для любых р1 < р2
< i ( p2 ) < i p1 ) < i.
28
3.4.Текущая стоимость
Впредыдущих разделах была выведена формула накопления капитала по известной силе процента:
t |
(3.20) |
|
A P exp (t)dt ,
0
где Р – начальный капитал; А – накопленная стоимость. Чтобы найти текущую стоимость, достаточно воспользоваться формулой (3.20)
и найти Р:
|
t |
(3.21) |
|
|
|
P Aexp |
|
(t)dt . |
|
0 |
|
Пусть накопленная стоимость А = 1. В этом случае величину Р обозначим через V(t):
|
t |
(3.22) |
V (t) exp |
|
(t)dt . |
|
0 |
|
Таким образом, V(t) – это текущая стоимость суммы 1, накопленной
за время t.
Замечание. Формула (3.20) и, следовательно, формула (3.21) были
выведены в случае, когда (t) является непрерывной функцией. Мате-
матически точно можно показать, что формула (3.20) остаётся верной,
когда (t) кусочно-непрерывная, в частности, кусочно-постоянная.
Пример 3.7. Пусть сила процента равна 6 %. Найти текущую стои-
мость суммы 100 у.д.е., выплачиваемой через 20 лет.
Решение. По формуле (3.21)
20
P 100exp 0,06dt 100  e 20 0,06100
e 20 0,06100  e1,2 36,79у.д.е.
e1,2 36,79у.д.е.
0
Пример 3.8. А. Пусть сила процента в банке А является кусочно-
постоянной:
29
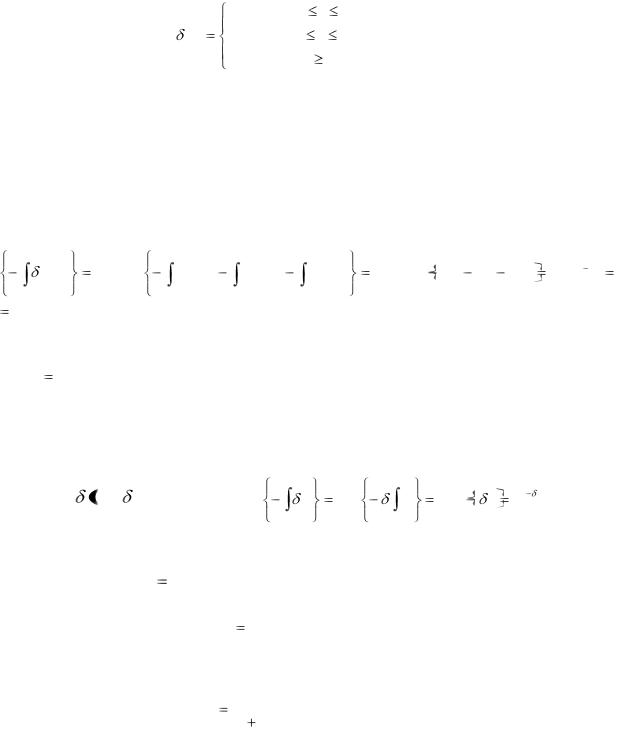
|
0,08, |
0 |
t |
5, |
(t) |
0,06, |
5 |
t |
10, |
|
0,04, |
|
t |
10. |
Какая сумма дает за 20 лет накопленную стоимость 250 у.д.е.?
Б. Банк Б выплачивает проценты по фактической ставке 6 % в год в течение 20 лет. В какой банк следует поместить деньги, чтобы за 20 лет получить максимальный доход?
Решение: А. Воспользуемся формулой (3.21) : P = 250 exp
20 |
|
5 |
10 |
20 |
|
(t)dt |
250exp 0,08ве |
0,06dt |
0,04dt 250exp 0,4 0,3 0,4 250е 1,3 |
0 |
|
0 |
5 |
10 |
83,22 у.д.е. |
|
|
|
|
Б. Найдём текущую стоимость суммы 250 у.д.е. за 20 лет: Р = |
||||
250 |
77,95 |
у.д.е. |
|
|
|
|
|
||
1,06 20 |
|
|
||
|
|
|
|
|
Вывод: доход в банке А выше.
Рассмотрим практически важный частный случай, когда сила процента
постоянна, t 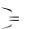 . При этом exp
. При этом exp
Обозначим exp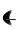
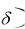 V , тогда
V , тогда
t |
|
t |
|
|
dt |
exp |
dt |
exp |
t (e )t . |
0 |
|
0 |
|
|
V (t) V t |
(3.23) |
для любых t > 0. На основании (3.10) формула (3.23) принимает вид
V (t) |
1 |
|
. |
(3.24) |
(1 |
i)t |
|
Все вышесказанное можно выразить в терминах учётной ставки, если вспомнить соотношение. Тогда V(t) = (1 – d)t.
30

3.5 Формула Студли для силы процента
Важным примером математической формулы для силы процента является формула Студли, которую можно записать в виде
(t) p |
S |
, |
|
||
1 r est |
||
|
|
(3.25) |
где p,s,r – параметры, которые определяются по заданной статистике.
Сила процента, определяемая формулой (3.25), обладает важным свойством: текущая стоимость любой суммы равна средневзвешенной текущих стоимостей двух сумм при различных постоянных значениях силы процента. Действительно,
|
|
t |
|
|
|
|
|
|
|
|
t |
|
|
s |
|
|
|
|
|
|
|
t |
|
|
rse sy |
|
|
|
|
||||
V (t) |
exp |
( у)dу |
exp |
( p |
|
|
|
|
|
|
)dy |
exp |
( p s |
|
|
|
|
|
|
)dy |
|
||||||||||||
1 |
r |
est |
|
1 |
r |
esy |
|
|
|||||||||||||||||||||||||
|
|
0 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
dre sy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
exp |
( p |
s)t |
|
|
|
|
exp |
|
( p |
s)t |
|
exp In(1 |
re sy ) |
t |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
1 |
|
r |
esy |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
||
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
exp |
( p |
s)t exp In(1 |
re st ) |
In(1 |
|
|
r) |
|
exp |
( p |
s)t |
1 re st |
|
|
1 |
|
|
1 |
|
x |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
1 |
r |
1 |
|
r |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
x exp |
( p |
s)t |
|
|
|
r |
|
exp pt |
1 |
|
|
V t |
|
|
1 |
V t , |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
1 |
|
|
r |
|
|
1 |
r |
1 |
1 |
|
r |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
где V |
e ( p |
s) ,V |
2 |
|
|
e p . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Итак, если сила процента (t) определяется формулой Студли (3.25), то
дисконтирующий множитель V(t) находится по формуле V(t) =
1 |
|
е p s t |
|
r |
|
e p t . |
|
|
|
|
|
||
1 |
r |
1 |
r |
|||
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ
1.Каково экономическое содержание понятия силы процента?
2.Каковы формулы накопления и дисконтирования в схеме непрерывных процентов?
31
