
Министерство образования Российской Федерации
Хабаровская государственная академия экономики и права
Кафедра естественнонаучных дисциплин
ФИЗИКА
Методические указания к лабораторному практикуму для
студентов 1 курса коммерческого факультета,
обучающихся по специальности 060800 и 351100
Хабаровск 2001

2
ББК В 3 Х 12
Составители: к. ф.-м. н. О.Д. Шереметьев Рецензент: доцент ДВГУПС, к.т.н. О.Г. Заволока
Утверждено издательскобиблиотечным академии в качестве методических указаний для студентов
ФИЗИКА Методические указания к лабораторному практикуму
для студентов 1 курса коммерческого факультета, обучающихся по специальности 060800 и 351100
ЛР № 020756 от 02.0498 г.
Редактор Г.С. Одинцова
Подписано в печать__________. Формат 60Х84/16 |
Бумага писчая. |
|
Печать офсетная. Усл. п.л. |
Уч.-изд.л. |
Тираж 60 экз. |
680042, г.Хабаровск, ул. Тихоокеанская, 134 ХГАЭП, РИЦ.
© Хабаровская государственная академия экономики и права, 2001
3
Лабораторная работа №1
Обработка и анализ результатов измерений
Цель работы: изучение методов измерения физических величин, практических приемов обработки и анализа результатов измерений.
Краткая теория: методы измерения физических величин. Погрешности измерений
Измерение в широком смысле слова — это операция, посредством которой устанавливается численное соотношение между, измеряемой величиной и заранее выбранной мерой. Мы будем рассматривать измерение физических величин.
Физическая величина — это свойство, общее в качественном отношении многим объектам (физическим системам, их состояниям и происходящим в них процессам), но в количественном отношении — индивидуальное для каждого физического объекта.
Измерить физическую величину — это значит сравнить ее с другой, однородной величиной, принятой за единицу измерения.
Для измерения физических величин применяются различные технические средства, специально для этого предназначенные и имеющие нормированные метрологические свойства. Поясним некоторые из указанных средств измерений. Мера — это средство измерений в виде тела или устройства, предназначенного для воспроизведения величин одного или нескольких размеров, значения которых известны с необходимой для измерений точностью. Примером меры могут служить гиря, измерительная колба, масштабная линейка.
В отличие от меры измерительный прибор не воспроизводит известное значение величины. Измеряемая величина в нем преобразуется в показание или сигнал, пропорциональный измеряемой величине в форме, доступной для непосредственного воспроизведения. Примером измерительного прибора могут служить амперметр, вольтметр, термопара и пр.
Измерения физических величин могут отличаться друг от друга особенностями технического или методического характера. С методической точки зрения измерения физических величин поддаются определенной систематизации. Их можно, например, подразделять на прямые и косвенные.
Если измеряемая величина непосредственно сравнивается с соответствующей единицей ее измерения или определяется путем отсчета показаний измерительного прибора, градуированного в соответственных единицах, то такое измерение называется прямым. Например, измерения толщины проволоки микрометром, промежутка времени секундомером, силы тока амперметром являются прямыми.
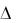
4
Большинство физических величин измеряется косвенным путем. Косвенным называется такое измерение, при котором искомая физическая величина непосредственно не измеряется, а вычисляется по результатам прямых измерений некоторых вспомогательных величин, связанных с искомой величиной определенной функциональной зависимостью.
При любых измерениях физических величин получаются результаты, которые неизбежно содержат погрешности (ошибки). Эти погрешности обусловлены самыми разнообразными причинами (несовершенство мер и измерительных приборов, несовершенство наших чувств). Результаты измерений являются поэтому лишь приближенными, более или менее близкими к истинным значениям измеряемых величин.
Разность между истинным значением измеряемой величины х и фактически измеренным х' называется истинной абсолютной погрешностью, или ошибкой измерения:
х = х - х’. |
(1) |
Отношение истинной абсолютной погрешности к истинному значению измеряемой величины х называется истинной относительной погрешностью измерения:
E = |
х |
. |
(2) |
|
|||
|
х |
|
|
Относительная погрешность—величина отвлеченная, она выражается в долях единицы или в процентах и поэтому позволяет сравнивать точность независимых друг от друга измерений (например, точность измерения диаметра и высоты цилиндра).
Так как никакое измерение не может дать истинного значения измеряемой величины, то задачей измерения любой физической величины является нахождение приближенного наиболее вероятного значения этой величины, а также определение и оценка допущенной при этом погрешности.
Погрешности (ошибки), которые имеют место при измерении физических величин, подразделяются на три группы: грубые, систематические, случайные. Грубые ошибки (промахи) — это ошибки, явно искажающие результаты измерений. Причинами грубых ошибок могут быть неисправности экспериментальной установки или измерительного прибора. Но чаще всего это следствие ошибок самого экспериментатора: неправильное определение цены деления измерительного прибора, неверный отсчет делений по шкале прибора, ошибочная запись результатов прямых измерений и т. п. В дальнейшем изложении будем предполагать, что измерения не содержат грубых ошибок (промахов).
Систематические погрешности обусловлены действием постоянных по величине и направлению факторов. Например, неточностью изготовления мер, неправильной градуировкой шкал или неправильной установкой измерительных приборов, а также постоянным и односторонним воздействием

5
на измеряемую величину или измерительную установку какого-либо внешнего фактора.
При повторных измерениях данной величины в одинаковых условиях систематическая погрешность каждый раз повторяется, имея одну и ту же величину и знак, или изменяется по определенному закону. При внимательном анализе принципа действия применяемых приборов, методики измерения и окружающих условий, систематические погрешности можно либо исключить в самом процессе измерения, либо учесть в окончательном результате измерений, внеся соответствующую поправку.
Случайные погрешности обусловлены действием большого числа самых разнообразных, как правило, переменных факторов, в своем большинстве не поддающихся учету и контролю и проявляющихся в каждом отдельном измерении по-разному. В силу неупорядоченности совокупного действия этих факторов предвидеть появление случайной погрешности и предугадать ее величину и знак невозможно. Погрешность такого рода потому и называется случайной, что появление ее — дело случая, появление ее не вытекает из данных условий эксперимента. Она может быть, а может и не быть.
Случайные погрешности проявляют себя в том, что при неизменных условиях эксперимента и при полностью исключенных систематических погрешностях результаты повторных измерений одной и той же величины оказываются несколько отличающимися друг от друга. Случайные погрешности по указанным выше причинам не могут быть исключены из результатов измерений как, например, погрешности систематические.
Среднее арифметическое значение, средняя квадратичная и средняя арифметическая погрешности измеряемой величины
Первой величиной, которую приходится вычислять при обработке результатов опытов, является среднее арифметическое из результатов ряда
|
|
|
1 |
|
n |
|
|
|
|
|
|
||||
измерений, которое определяется по формуле |
х |
|
|
xi . |
(3) |
||
n i |
|||||||
|
|
|
1 |
|
|||
Практически число измерений всегда ограничено, |
поэтому |
среднее |
|||||
арифметическое Χ не равно истинному значению измеряемой величины х, но будет тем ближе к нему, чем больше число выполненных измерений п. В теории вероятностей доказывается, что среднее арифметическое из результатов отдельных измерений является наиболее вероятным значением измеряемой величины. Это утверждение справедливо при условии, когда все измерения равноточные, а распределение погрешности измерений подчиняется закону распределения Гаусса.
Если вместо истинного значения неизвестной величины использовать
среднее арифметическое Χ , тогда на основании равенства (1) имеем:
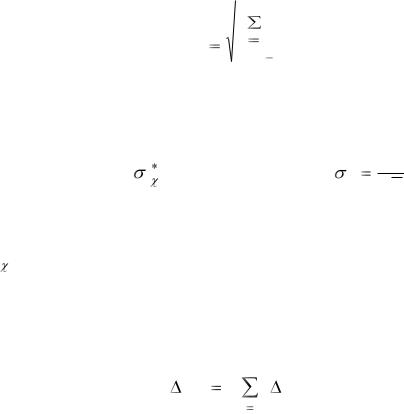
6
|
|
|
|
|
|
|
|
|
|
|
х1 = Χ |
|
- |
х1 |
|
||||
|
|
|
|
|
|
|
|||
• |
х2 = Χ |
• |
- |
х2 |
|
||||
• |
• |
• |
• |
• |
|
||||
• |
• |
• |
• |
• |
• |
• |
(4) |
||
• |
• |
• |
• |
• |
• |
• |
|||
|
|||||||||
|
|
|
|
|
|
|
|||
|
хn = Χ |
|
- |
хn |
|
||||
В (4) погрешность хi, несколько отличается от истинной и называется
|
|
|
|
абсолютной погрешностью единичного измерения хi = Χ - хi . |
(5) |
||
Лучшим из критериев для оценки погрешностей результатов измерений является средняя квадратичная погрешность, которая характеризует степень (меру) рассеяния результатов отдельных измерений (хi) около среднего их значения. Для определения среднеквадратической погрешности единичных измерений при ограниченном числе опытов используется
|
|
|
n |
|
|
|
|
|
|
Δxi2 |
|
|
|
S´х |
i |
1 |
. |
(6) |
||
|
n 1 |
|||||
|
|
|
|
|
|
|
Средняя квадратическая погрешность, вычисляемая по формуле (6), характеризует погрешность единичного результата из всего ряда n измерений.
Как уже отмечалось, при увеличении числа n измерений наблюдается взаимная компенсация случайных ошибок. Поэтому усредненная средняя
квадратичная погрешность |
|
, определяемая как |
* |
|
х |
||
|
|
|
S ' x и характеризу- 
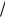 n
n
ющая окончательный результат измерений, уменьшается при увеличении числа n повторных измерений искомой величины. Так как вычисления ве-
личины 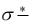 достаточно громоздки, то в ряде случаев, если не оговорено в
достаточно громоздки, то в ряде случаев, если не оговорено в
условиях решаемой задачи, для оценки ошибки, допущенной при определении средней величины, пользуются средней арифметической погрешностью, которая вычисляется как средняя величина всех величин абсолютных погрешностей единичных измерений (12), взятых по модулю:
|
1 |
|
n |
|
|
хср |
|
|
/ хi / . |
(7) |
|
n i |
|||||
|
1 |
|
|||
Так как суммирование в (7) выполняется без учета знака ∆хi , то формула
(7) дает среднее значение максимально возможной погрешности.
Вопрос о том, какой формулой пользоваться при оценке измерений, решается при планировании эксперимента. Считается, что при числе измерений меньше пяти можно ограничиться вычислением средней абсолютной погрешности по формуле (7).
Средняя абсолютная погрешность дает возможность указать пределы (интервал), внутри которых заключено истинное значение измеряемой величины.
Сама по себе абсолютная погрешность не дает достаточно наглядного представления о степени точности измерения, поэтому, как отмечалось вы-
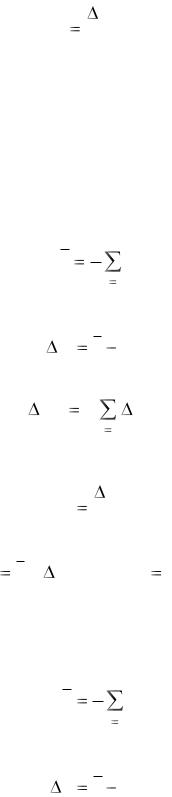
7
ше, для оценки точности результата применяется относительная погрешность. Относительная погрешность величины х при ограниченном числе опытов вычисляется по формуле
E |
хср |
. |
(8) |
||
|
|
|
|||
|
х |
||||
|
|
|
|
||
Обработка результатов прямых измерений
В общем случае порядок обработки результатов прямых измерений следующий (предполагается, что систематических ошибок нет).
Случай 1. Число измерений меньше пяти
1.По формуле (3) находится средний результат х, определяемый как среднее арифметическое от результатов всех измерений, т. е.
1 1
хn i 1 хi .
2.По формуле (4) вычисляются абсолютные погрешности отдельных измерений:
хi х хi .
3. По формуле (7) определяется средняя абсолютная погрешность:
хср |
1 |
|
n |
|
хi |
|
. |
|
|
|
|
||||||
|
|
|
|
|
||||
n i |
1 |
|||||||
|
|
|
|
|
||||
4. По формуле (8) вычисляют среднюю относительную погрешность результата измерений:
Eх |
хср |
. |
||
|
|
|
||
|
х |
|||
|
|
|
||
5. Записывают окончательный результат по следующей форме:
х х 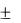 хср , при Ех ....%
хср , при Ех ....%
Случай 2. Число измерений свыше пяти
1.По формуле (3) находится средний результат:
1 n
хn i 1 xi
2.По формуле (4) определяются абсолютные погрешности отдельных измерений:
хi x xi
3. По формуле (6) вычисляется средняя квадратическая погрешность единичного измерения:
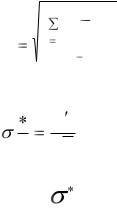
8
|
n |
|
|
|
|
( х |
х )2 |
|
|||
S´х |
1 |
|
i |
. |
|
|
i |
|
|
|
|
|
|
n |
1 |
|
|
4. Вычисляется среднее квадратическое отклонение для среднего значения измеряемой величины по формуле:
S х .
х 
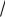 n
n
5. Записывается окончательный результат по следующей форме
х 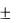 х .
х .
Иногда случайные погрешности измерений могут оказаться меньше той величины, которую в состоянии зарегистрировать измерительный прибор (инструмент). В этом случае при любом числе измерений получается один и тот же результат. В подобных случаях в качестве средней абсолютной погрешности хср принимают половину цены деления шкалы прибора (инструмента). Эту величину иногда называют предельной или приборной погрешностью и обозначают хпр (для нониусных приборов и секундомера хпр равна точности прибора).
Оценка достоверности результатов измерений
В любом эксперименте число измерений физической величины всегда по тем или иным причинам ограничено. В связи с этим может быть поставлена задача - оценить достоверность полученного результата. Иными словами, определить, с какой вероятностью можно утверждать, что допущенная при этом ошибка не превосходит наперед заданную величину ε. Упомянутую вероятность принято называть доверительной вероятностью. Обозначим ее буквой Рα.
Может быть, поставлена и обратная задача - определить границы интервала ±ε, чтобы с заданной вероятностью Рα можно было утверждать, что истинное значение измерений величины х не выйдет за пределы указанного так называемого доверительного интервала.
Доверительный интервал характеризует точность полученного результата, а доверительная вероятность — его надежность. Методы решения этих двух групп задач имеются и особенно подробно разработаны для случая, когда погрешности измерений распределены по нормальному закону. Теория вероятностей дает также методы для определения числа опытов (повторных измерений), при которых обеспечивается заданная точность и надежность ожидаемого результата. В данной работе эти методы не рассматриваются (ограничимся только их упоминанием), так как при выполнении лабораторных работ подобные задачи обычно не ставятся.
Особый интерес, представляет случай оценки достоверности результата измерений физических величин при весьма малом числе повторных измерений. Например, n<10. Это именно тот случай, с которым мы часто встреча-
9
емся при выполнении лабораторных работ по физике. При решении указанного рода задач рекомендуется использовать метод, в основе которого лежит распределение (закон) Стьюдента.
Для удобства практического применения рассматриваемого метода имеются таблицы, с помощью которых можно определить доверительный интервал ±ε, соответствующий заданной доверительной вероятности Рα или решить обратную задачу.
Ниже приведены те части упомянутых таблиц, которые могут потребоваться при оценке результатов измерений на лабораторных занятиях.
Пусть, например, произведено n равноточных (в одинаковых условиях) измерений некоторой физической величины х и вычислено ее среднее зна-
чение х . Требуется найти доверительный интервал ε, соответствующий заданной доверительной вероятности Рα. Задача в общем виде решается так.
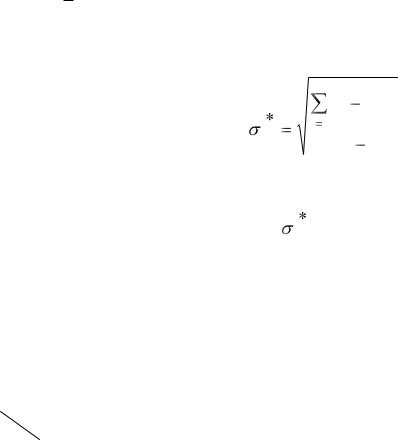
По формуле с учетом (6) вычисляют
|
|
|
n |
|
|
|
|
|
|
|
|
(х |
хi )2 |
||||
|
|
i |
1 |
|
|
|
. |
|
х |
n(n |
1) |
||||||
|
||||||||
Затем для заданных значений n и Рα. находят по табл.1 величину tc . Искомое значение ε в вычисляется на основе формулы
ε = |
|
tc . |
(9) |
|
|||
|
х |
|
|
При решении обратной задачи вначале вычисляют по формуле (9) параметр tc. Искомое значение ε доверительной вероятности Рα берется из табл. 2 для заданного числа n и вычисленного параметра tс.
Таблица 1
Значение параметра tc при заданном числе опытов n и доверительной вероятности Рα
Рα |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
0,95 |
0,98 |
0,99 |
0,995 |
0,999 |
|
n |
|||||||||||
|
|
|
|
|
|
|
|
|
|
||
2 |
1,000 |
1,376 |
1,963 |
3,08 |
6,31 |
12,71 |
31,8 |
63,7 |
127,3 |
637,2 |
|
3 |
0,816 |
1,061 |
1,336 |
1,886 |
2,91 |
4,30 |
6,96 |
9,92 |
14,1 |
31,6 |
|
4 |
0,765 |
0,978 |
1,250 |
1,638 |
2,35 |
3,18 |
4,54 |
5,84 |
7,5 |
12,94 |
|
5 |
0,741 |
0,941 |
1,190 |
1,533 |
2,13 |
2,77 |
3,75 |
4,60 |
5,6 |
8,61 |
|
6 |
0,727 |
0,920 |
1,156 |
1,476 |
2,02 |
2,57 |
3,36 |
4,03 |
4,77 |
6,86 |
|
7 |
0,718 |
0,906 |
1,134 |
1,440 |
1,943 |
2,45 |
3,14 |
3,71 |
4,32 |
5,96 |
|
8 |
0,711 |
0,896 |
1,119 |
1,415 |
1,895 |
2,36 |
3,00 |
3,50 |
4,03 |
5,40 |
|
9 |
0,706 |
0,889 |
1,108 |
1,397 |
1,860 |
2,31 |
2,90 |
3,36 |
3,83 |
5,04 |
|
10 |
0,703 |
0,883 |
1,110 |
1,383 |
1,833 |
2,26 |
2,82 |
3,25 |
3,69 |
4,78 |
|
|
|
|
|
|
|
|
|
|
|
|
10
|
|
|
|
|
Таблица 2 |
|
Значение доверительной вероятности Рα при заданном |
|
|||
|
|
числе опытов n и параметре tc |
|
||
№ |
2 |
2,5 |
3 |
|
3,5 |
2 |
0,705 |
0,758 |
0,795 |
|
0,823 |
3 |
0,816 |
0,870 |
0,905 |
|
0,928 |
4 |
0,861 |
0,912 |
0,942 |
|
0,961 |
5 |
0,884 |
0,933 |
0,960 |
|
0,975 |
6 |
0,898 |
0,946 |
0,970 |
|
0,983 |
7 |
0,908 |
0,953 |
0,976 |
|
0,987 |
8 |
0,914 |
0,959 |
0,980 |
|
0,990 |
9 |
0,919 |
0,963 |
0,983 |
|
0,992 |
10 |
0,923 |
0,969 |
0,985 |
|
0,939 |
Обработка результатов косвенных измерений
Очень редко содержание лабораторной работы или научного эксперимента сводится к получению результата прямого измерения. Большей частью искомая величина является функцией нескольких других величин.
Задача обработки опытов при косвенных измерениях заключается в том, чтобы на основании результатов прямых измерении некоторых величин (аргументов), связанных с искомой величиной определенной функциональной зависимостью, вычислить наиболее вероятное значение искомой величины и оценить погрешность косвенных измерений.
Существует несколько способов обработки косвенных измерений. Рассмотрим следующие два способа.
Пусть по методу косвенных измерений определяется некоторая физическая величина R = f (x, y, z,…). Результаты прямых измерений ее аргументов х, у, z приведены в табл. 3.
Таблица 3
Номер опыта |
x |
y |
z |
• • |
• |
|
|
|
|
||
|
|
|
|
|
|
1 |
х1 |
y1 |
z1 |
• • |
• |
2 |
х2 |
y2 |
z2 |
• • |
• |
• |
|
||||
• |
• |
• |
• |
|
|
|
|
||||
• |
• |
• |
• |
• |
|
• |
• |
• |
• |
• |
|
n |
хn |
yn |
zn |
|
|
• • |
• |
||||
|
|
|
|
|
|
Первый способ обработки результатов заключается в следующем. С помощью расчетной формулы вычисляют искомую величину по результатам каждого опыта
R1 = f(x1,y1,z1,…)
R2 |
= f(x2,y2,z2,…) |
||||||||
• |
• |
• |
• |
• |
• |
• |
• |
• |
• |
• |
• |
• |
• |
• |
• |
• |
• |
• |
• |
• |
• |
• |
• |
• |
• |
• |
• |
• |
• |
Rn = f(xn,yn,zn,…)
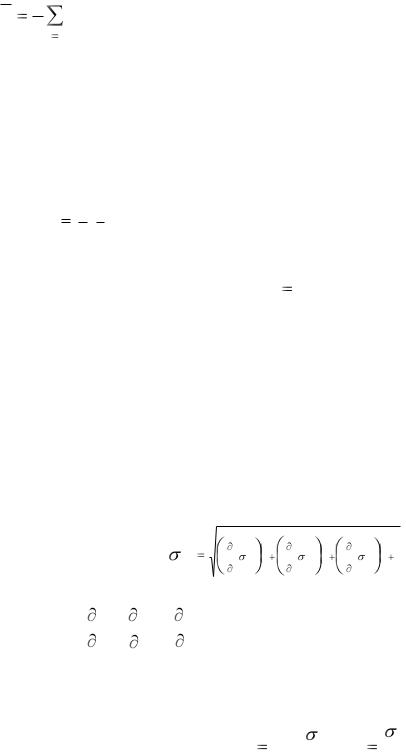
11
Далее обычным методом можно вычислить ее наивероятнейшее значение
1 n
R Ri , а также среднюю погрешность, используя формулы (7). n i 1
Описанный способ обработки результатов применим, в принципе, во всех без исключения случаях косвенных измерений. Однако наиболее целесообразно применять его тогда, когда число повторных измерений аргументов небольшое, а расчетная формула косвенно измеряемой величины сравнительно проста.
При втором способе обработки результатов опытов вначале вычисляют, используя результаты прямых измерений (табл. 3), средние арифметические значения каждого из аргументов, а также погрешности их измерения. Под-
ставив x, y, z, ... в расчетную формулу, определяют наиболее вероятное значение измеряемой величины
|
|
|
|
|
|
|
|
|
R f (x, y, z,...) |
(10*) |
|||||||
и выполняют оценку результатов косвенных измерений величины.
Второй способ обработки результатов применим лишь к таким косвенным измерениям, при которых истинные значения аргументов от измерения к измерению остаются постоянными.
Погрешности косвенных измерений величины R = f (x, y, z,…) зависят от погрешностей прямых измерений ее аргументов.
Если систематические погрешности измерений аргументов исключены, а случайные погрешности измерения этих аргументов нe зависят друг от друга (некореллированы), то ошибка косвенного измерения величины R определяется в общем случае по формуле
|
|
|
|
|
|
|
f |
2 |
f |
2 |
f |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
.. …… .. , |
(11) |
|||
|
|
|
|
|
R |
|
|
x |
|
y |
|
z |
||
|
|
|
|
|
|
x |
y |
z |
||||||
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
где |
f |
; |
f |
; |
f |
- частные производные; |
|
|||||||
x |
y |
z |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
σx, σy, σz - средние квадратические погрешности измерения аргументов х, у, z, ... .
Относительная погрешность вычисляется по формуле
ER |
|
|
|
R |
|
|
|
R |
|
. |
(12) |
|||||
|
|
|
|
|
|
|
|
|
|
|
||||||
f (x, y, z,...) |
R |
|||||||||||||||
|
|
|
|
|||||||||||||
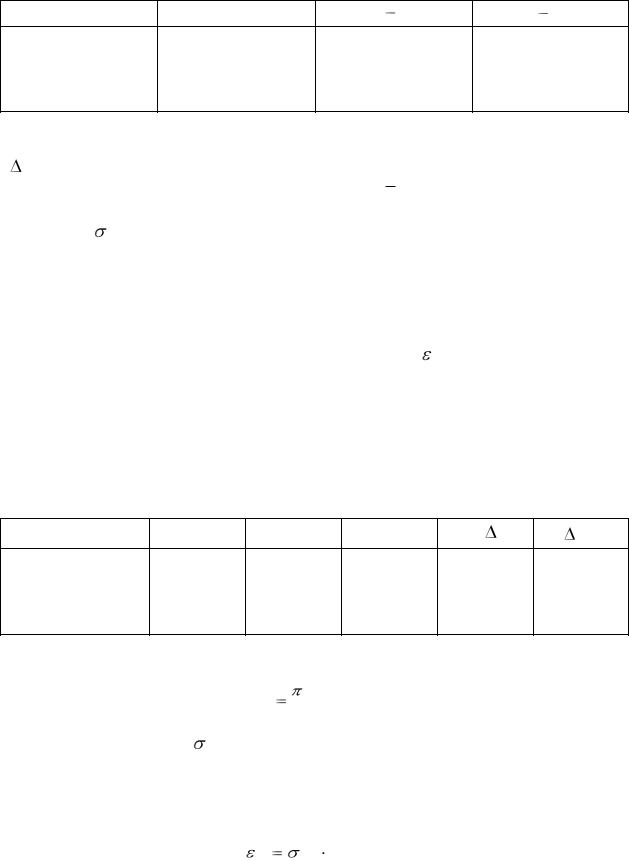
В ряде случаев значительно проще (с точки зрения обработки результатов измерений) вычислить вначале относительную погрешность ER, а затем, используя формулу (12), абсолютную погрешность результата косвенного измерения:

12
|
|
|
|
R ER R . |
(13) |
||
При этом формулы для вычисления относительной погрешности результата составляются в каждом отдельном случае в зависимости от того, каким образом искомая величина связана своими аргументами. Имеются таблицы формул относительных погрешностей для наиболее часто встречающихся видов (структуры) расчетных формул (табл. 4).
Таблица 4
Определение относительной погрешности ER, допускаемой при вычислении приближенной величины R, зависящей от приближенной А, В, С
Характер связи главной величины |
Формула для определения |
||||||||||||||
с приближенными величинами |
относительной погрешности |
||||||||||||||
Сумма: А+В |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
( |
А) |
2 |
( |
|
В) |
2 |
|
||||||||
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А В |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Разность: А-В |
( |
А)2 |
( |
|
В)2 |
||||||||||
|
|
|
|
|
А В |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
Произведение: А·В |
|
|
|
А 2 |
|
|
В 2 |
||||||||
|
|
|
А |
|
|
|
|
|
В |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
А |
|
|
|
|
|
|
|
|
|
|
||||
Частное: |
|
|
|
А 2 |
|
|
В 2 |
||||||||
В |
|
|
|
|
А |
|
|
|
|
|
В |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Степень: Аm |
|
|
|
m |
|
A |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
A |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Изучение нониусов
Измерение длины производится с помощью масштабных линеек. Для увеличения точности измерения пользуются вспомогательными подвижными шкалами – нониусами. Например, если масштабная линейка разделена на миллиметры, т. е. цена одного деления линейки 1 мм, то с помощью нониуса можно повысить точность измерений по ней до одной десятой или более мм.
Нониусы бывают линейными и круговыми. Разберем устройство линейного нониуса. На нониусе m делений, которые в сумме равны – 1 делению основной шкалы. Если a – цена деления нониуса, b – цена деления масштабной линейки, то можно написать
a m =(m-1)b .
Отношение |
b |
b a называется точностью нониуса. |
|
m |
|||
|
|
Если, например, b=1 мм, а m=10, то точность нониуса 0,1 мм. Искомая длина тела равна:
L = k b + L , |
(14) |

13
где k – целое число делений масштабной линейки;
ΔL – число делении миллиметра, которое необходимо определить с помощью нониуса.
Обозначим через n - число делений нониуса, совпадающее с любым де-
лением масштабной линейки. |
|
|
|
|
|
Следовательно, |
L nb na n(b |
a) n |
b |
0,1n |
. |
|
m |
|
|||
Таким образом, длина измеряемого тела равна целому числу k мм масштабной линейки плюс десятые доли числа миллиметров. Аналогично устроены и круговые нониусы.
Нижняя шкала наиболее распространенного микрометра представляет собой обычную миллиметровую шкалу.
Ризки верхней шкалы сдвинуты по отношению к ризкам нижней шкалы на 0,5 мм. При повороте микрометрического винта на 1 оборот барабан С вместе со всем винтом передвигается, на 0,5 мм, открывая или закрывая поочередно ризки то верхней, то нижней шкалы. Шкала на барабане содержит
50 делений, таким образом, точность микрометра |
b |
|
0,5 |
0,01мм . |
|
m 50 |
|||||
|
|
||||
При отсчете по микрометру необходимо учитывать целое число ризки верхней и нижней шкалы k (умножая это число на 0,5 мм) и номер деления барабана n, который в момент отсчета совпадает с осью шкалы стебля D, умножая его на точность микрометра. Иными словами, числовое значение L длины измеряемого микрометром предмета находят по формуле
L 0,5k |
|
n |
мм |
(15) |
100 |
|
|||
Для того чтобы измерить длину предмета или диаметр отверстия штангенциркулем, следует поместить предмет между неподвижной и подвижной ножками C и D или развести выступы АВ по диаметру внутри измеряемого отверстия. Движение перемещающегося устройства штангенциркуля проводится без сильного нажима. Вычисление длины производят по формуле (15), снимая отсчет по основной шкале и нониусу.
Вмикрометре для измерения длины предмет зажимают между упором А
имикрометрическим винтом В, вращая последний только с помощью головки Е.
Длину измеряемого предмета находят с помощью формулы (15), используя показания линейной шкалы D и шкалы барабана С.
Порядок проведения работы
Задание 1. Измерение диаметра проволоки с помощью микрометра.
1. Измерьте не менее 7 раз диаметр проволоки в разных местах. Результаты занести в табл. 5.
14
Таблица 5
|
|
|
|
|
|
|
d i ) 2 |
Номер измерения |
d |
d d |
i |
( |
d |
||
|
|
|
|
|
|
|
|
1
·
·
·
7
2.Определите границу допускаемой абсолютной ошибки микрометра
хпр (приборная ошибка).
3.Вычислите среднее значение диаметра d , среднеквадратическое от-
клонение |
* |
по формулам методики обработки результатов прямых изме- |
|
d |
|||
|
|
рений (случай 2).
4. Определите границу доверительного интервала для заданной доверительной вероятности Pa (задается преподавателем) и числа опытов n. Сравните приборную погрешность с доверительным интервалом. В окончательный результат запишите большее значение d  d
d
Задание 2. Определение объема цилиндра с помощью микрометра и штангенциркуля.
1. Измерьте не менее 7 раз диаметр цилиндра микрометром, а высоту штангенциркулем. Результаты измерений запишите в таблицу (табл. 6).
Таблица 6
Номер измерения |
D |
h |
V |
Vi |
Vi |
2 |
1
·
·
·
7
2. Определите объем цилиндра для каждого отдельного измерения
|
|
|
|
D 2 h |
. |
(16) |
|
|
|
Vi |
i i |
||
|
|
|
|
|
||
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
3. Определите Vcр и |
|
* |
по формулам методики обработки |
|
||
V |
|
|||||
|
|
|
|
|
||
результатов прямых измерений (случай 2).
4. Определите доверительный интервал Ε< для косвенно измеряемой величины по заданной доверительной вероятности Ра, и числу опытов n.
|
* |
t. cт. |
||
V |
|
|
||
V |
||||
|
|
|||
