
- •Министерство образования Российской Федерации
- •Хабаровская государственная академия экономики и права
- •КОРРЕЛЯЦИОННО-РЕГРЕССИОННЫЙ АНАЛИЗ И ПРОГНОЗИРОВАНИЕ
- •1. Задача
- •Задания для выполнения лабораторной работы
- •Щелкнув мышью по первой строке Numeric Data, появится список (рис.6):
- •Выберем второй пункт Multiple – Variable Analysis, откроется диалоговое окно для ввода переменных (рис.7).
- •Таблица 1
- •Таблица 2
- •Таблица 4
- •Таблица 10
- •Таблица 11
- •Уравнения линейных трендов
- •Таблица 15
- •Таблица 16
- •Таблица 17
- •Прогнозные расчеты
- •Ход работы
- •Анализ матрицы коэффициентов корреляции
- •Варианты заданий
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Вариант 11
- •Вариант 12
- •Вариант 13
- •Вариант 15
- •Критические точки распределения Стъюдента
- •Приложение 3
- •Окончание прил. 4
- •Библиографический список
- •ВОПРОСЫ И ЗАДАНИЯ ДЛЯ ЗАЩИТЫ ЛАБОРАТОРНОЙ РАБОТЫ
- •Корреляционно-регрессионный анализ и прогнозирование
- •Подписано в печать . Формат 60х84/16. Бумага писчая.
- •Выписка из протокола № 7

24
Щелкните мышью по кнопке строки Plot Fitted Model, затем по кнопке ОК, появится график (рис.21).
Рис. 21
Ход работы
3.1. Оценка параметров распределения 3.1.1. Точечные оценки представим в табл. 20.
|
|
|
|
|
|
Таблица 20 |
|
|
|
|
|
|
|
|
|
|
Средняя х |
С.К.О |
Дисперсия |
Коэффициент |
|
x |
|||||
|
|
S |
S2 |
вариации |
||
Y |
301,667 |
104,322 |
10883,1 |
34,58% |
||
X1 |
7,027 |
2,62 |
6,87 |
37,32% |
||
X2 |
15,83 |
0,66 |
0,44 |
4% |
||
X3 |
105,413 |
2,51 |
6,31 |
2% |
||
Средние, С.К.О, дисперсии, коэффициент вариации выпишем из распечатки (табл. 3).
Коэффициенты вариации Vy, Vx1, Vx2, Vx3 вычисляются по формуле
Vx |
100 |
S x |
||
|
|
|
||
|
x |
|||
|
|
|
||
Наибольшее рассеяние вокруг средних имеем ряд значений х1.
3.1.2. Рассчитаем интервальные оценки для средних значений и дисперсий генеральной совокупности.
Доверительный интервал для средних значений определяется по формуле
|
|
|
|
S x |
|
|
|
х х t |
|
|
|
||||
/ 2 |
|
|
, |
||||
|
N |
||||||
|
|
|
|
|
|||

25
где х , Sх , N – известны,
t /2 определяем по таблице критических значений распределения Стьюдента; =0,05 t /2=2,14 (прил. 2).
=N-1=15-1=14 - число степеней свободы.
У=301,667 57,7 |
243,96 |
У 359,367 |
||
х1=7,027 |
1,45 |
5,577 |
х1 |
8,477 |
х2=15,83 |
0,365 |
15,465 |
х2 |
16,195 |
х3=105,413 1,387 |
104,026 х3 106,8 |
|||
Доверительные интервалы для средних приведены в табл. 4. Доверителны границы дисперсий определяются из соотношения
|
|
S 2 |
N |
1 |
|
2 S 2 N |
1 |
|
||
|
|
x |
2 |
/ 2 |
|
|
x 2 |
/ 2 |
, |
|
|
|
|
N 1, |
|
|
N 1,1 |
|
|||
где S2 - выборочная дисперсия, |
|
|
|
|
||||||
N - объем выборки, |
=0,05. |
|
|
|
|
|
||||
2 |
2 |
|
|
|
|
|
|
|
2 – распределения |
|
N 1, / 2 |
и N 1,1 / 2 |
найдем по |
таблице |
|||||||
(прил. 1) , |
=0,05, N=15 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
26,1 |
2 |
|
5,63 |
||
|
N 1, |
/ 2 |
|
N 1,1 |
/ 2 |
|||||
|
|
|
|
|
||||||
5837,6 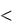
3,68 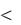
2
Y
2 x1
27061,6
17,68
Аналогично найдите доверительные для |
2 |
, |
2 |
х 2 |
х3 |
Доверительный интервал для у найден в табл. 7.
3.2.Корреляционный анализ
Из табл. 4 выпишем матрицу парных коэффициентов корреляции (см.
табл. 21).
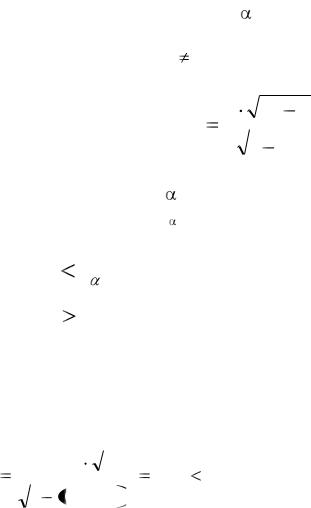
26
|
|
|
|
Таблица 21 |
|
|
|
|
|
|
Y |
X1 |
X2 |
X3 |
Y |
|
0,4384 |
0,8097 |
0,9364 |
X1 |
|
|
0,3184 |
0,5498 |
X2 |
|
|
|
0,8102 |
X3 |
|
|
|
|
Анализ матрицы коэффициентов корреляции
Проверим значимость полученных коэффициентов корреляции. При заданном уровне значимости =0,05 проверим гипотезу о
равенстве нулю генерального коэффициента корреляции Н0: rг-0 , при конкурирующей гипотезе Н1: rг 0.
Рассчитаем для каждого коэффициента t – статистику по формуле
t |
r |
N 2 |
|||
|
|
|
|
||
|
|
|
|
||
1 |
r 2 |
||||
|
|||||
По таблице критических точек распределения Стьюдента, при заданном уровне значимости =0,05 и числе степеней свободы N-2=13. Находим критическую точку t =2,16 по таблицам критических точек распределения Стьюдента (прил. 2).
Если |
|
|
t |
|
t |
|
нет оснований отвергнуть нулевую гипотезу Н0 |
|||||||||||
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
t |
|
t2 - Н0 отвергается, принимается гипотеза Н1, что |
|||||||||
|
|
|
|
|
|
|
|
|||||||||||
коэффициент корреляции rxi x j |
существенно отличен от нуля, т.е значим. |
|||||||||||||||||
Рассчитаем t для всех коэффициентов |
||||||||||||||||||
ryx |
1 |
, ryx |
2 |
, ryx |
3 |
, rx x |
2 |
, rx x |
3 |
, rx |
x |
3 |
||||||
|
|
|
|
|
|
1 |
|
1 |
2 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
t yx1 |
|
0,4384 |
13 |
|
|
1,77 |
2,16. |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|||||||
|
1 |
|
0,4384 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||

27
t yx |
4,94 |
2,16 |
|
2 |
|
t yx |
3,3 |
2,16 |
|
3 |
|
tx1x2 1,22 2,16 tx1x3 2,38 2,16 tx2 x3 495 2,16
Коэффициенты ryx1 , rx1x2 - незначимы.
Коэффициенты ryx2 , ryx3 , rx1x3 , rx2 x3 - значимы, следовательно, между
соответствующими показателями существует линейная зависимость, о тесноте связи можно судить по значению коэффициента корреляции, используя шкалу Чеддока (табл. 22).
|
|
|
|
|
|
|
Таблица 22 |
||
|
|
|
|
|
|
|
|
|
|
Показания |
|
|
|
|
|
|
|
|
|
тесноты |
0,1-0,3 |
0,3-0,5 |
0,5-0,7 |
0,7-0,9 |
0,9-0,99 |
||||
связи |
|
|
|
|
|
|
|
|
|
Характерис |
|
|
|
|
|
|
Весьма |
||
тика силы |
слабая |
|
|
умеренная |
заметная |
высокая |
высокая |
||
связи |
|
|
|
|
|
|
|
|
|
Тот факт, что r |
x |
|
0,8102 0,8 говорит о том, что показатели х |
2 |
и х |
||||
|
x |
3 |
|
|
|
|
3 |
||
|
2 |
|
|
|
|
|
|
|
|
коллинеарны и при моделировании зависимости объема реализации продукции y от х2 (цена за ед. продукции) и х3 (индекса потребительских цен) один из факторов можно отбросить как дублирующий.
3.3.Регрессионный анализ
Из табл. 8, 9, 10, 11, 12, 13, 14 выпишем уравнения множественной и
парной регрессий в натуральном масштабе. |
|
У= - 3862,2 – 3,51x1+18,24x2+36,99x3 |
(3.3.1) |
У= - 1612,33+8х1+117,33х2 |
(3.3.2) |
У= - 4029,32 – 4,35х1+41,37х3 |
(3.3.3) |
У= - 3639,97+23,37x2+33,88x3 |
(3.3.4) |
У= 179,067+17,44x1 |
(3.3.5) |
У= - 1715,58+127,405х2 |
(3.3.6) |
У= - 3796,63+38,87х3 |
(3.3.7) |
В стандартизированном масштабе уравнения регрессий имеют вид для парной :

где
y 0
xk0
28
|
|
|
|
|
|
|
|
ryxi xi |
xi |
|
|
|
|
У |
У |
||||||||
|
|
|
|
SУ |
|
S x |
|
|
|
||
|
|
|
|
|
|
|
|
i |
|
|
|
для множественной: |
|
|
|
|
|
|
|
|
|||
|
|
у 0 |
|
2 х10 |
3 х20 |
4 х30 , |
|||||
k вk |
Sx |
|
|
|
|
|
|
|
|
||
k |
|
|
|
|
|
|
|
|
|||
|
- стандартизированный коэффициент регрессии. |
||||||||||
|
S y |
|
|
|
|
|
|
|
|
||
|
y |
y |
|
|||
|
|
|
|
|
|
стандартизированное значение результативного признака y. |
|
|
- |
||||
|
S y |
|
||||
|
|
|
|
|
||
xk |
x k |
|
||||
|
|
|
- |
стандартизированное значение фактора xk. |
||
|
S x |
|
||||
|
k |
|
|
|
|
|
Выполнить самостоятельно.
3.3.2.Исследуем полученные уравнения на автокорреляцию остатков по критерию Дарбина – Уотсона.
Если автокорреляция отсутствует, то d 4, при полной автокорреляции d 0 и d 4. Для d-статистики найдены критические границы (dU - верхняя, dL – нижняя), позволяющие принять или отклонить гипотезу об отсутствии автокорреляции остатков при определенном уровне значимости =0,05. Составлена таблица значений этого критерия (прил. 3). Приведём часть этой таблицы (см. табл. 23).
Таблица 23
n |
m=1 |
m=2 |
m=3 |
m=4 |
m=5 |
|||||
|
dL |
dU |
dL |
dU |
dL |
dU |
dL |
dU |
dL |
dU |
15 |
1,08 |
1,36 |
0,95 |
1,54 |
0,82 |
1,75 |
0,69 |
1,97 |
0,56 |
2,21 |
где n – объем выборки, m – число факторов в уравнении регрессии.
Если вычисляемое значение d находится в пределах от dU до (4 – dU), то гапотеза об отстутствии автокорреляции не отклоняется, если же dL<d<dU или 4 – dU<d<4-dL, то нет статистических оснований ни принять, ни отклонить эту гипотезу (область неопределенности). Если d<dL или
d>4 – dL, то это указывает на наличие автокорреляции.
есть |
dL |
? |
dU |
нет |
4-dU |
? |
4-dL есть |
(-) |
|
|
|
|
|
|
(+) |
Составим шкалу для уравнения (3.3.1) |
|
|
|
||||
DL=0,71 |
dU=1,61 |
|
|
|
|
|
|
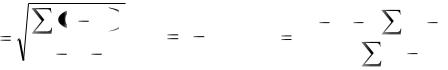
29
есть (-) |
0,71 |
|
1,61 |
|
2,39 |
|
3,29 есть (+) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dL |
? |
dU |
нет |
4-dU |
? |
4-dL |
||||
Расчетное значение dL=1,31 (см. табл. 8) попадает в область неопределенности. Вопрос о наличии и отсутствии автокорреляции не решен, с определенной долей риска это уравнение можно использовать для принятия решений на его основе. Аналогично проверьте гипотезу о наличии автокорреляции уравнений (3.3.2), (3.3.3), (3.3.4), (3.3.5), (3.3.6), (3.3.7).
3.3.3. Оценка точности уравнений регрессии.
Оценим точность полученных уравнений регрессии по стандартной ошибке (Sост), коэффициенту множественной детерминации (R2) и по статистическому критерию Фишера (F). Заполним табл. 24, используя данные таблицы (8, 9, 10, 11, 12, 13, 14).
|
|
|
Таблица 24 |
|
|
|
|
Уравнение |
Sост |
R2 |
F |
регрессии |
|
|
|
Y(x1x2x3) |
39,11 |
88,94 |
29,49 |
Y(x1x2) |
62,54 |
69,18 |
13,47 |
Y(x1x2) |
38,19 |
88,51 |
46,22 |
Y(x2x3) |
38,32 |
88,43 |
45,87 |
Y(x1) |
97,3 |
19,22 |
3,03 |
Y(x2) |
63,53 |
65,55 |
27,74 |
Y(x3) |
38,001 |
87,67 |
92,48 |
При расчете точности уравнений регрессии использовались формулы
|
|
y yˆ 2 |
|
S 2 |
|
|
|
|
|
|
|
||
|
|
; R 2 1 |
(n m 1) |
( yˆ |
|
|
y)2 |
||||||
S |
|
|
ост |
; F |
|
|
|
|
, |
||||
ост |
|
2 |
|
|
|
||||||||
n m 1 |
m |
( y |
yˆ ) |
2 |
|||||||||
|
|
|
S |
y |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||
где m – число зависимых переменных в выбранной модели, n – число наблюдений.
Наименьшую стандартную ошибку имеет уравнение регрессии y(х3). Наибольший коэффициент множественной детерминацией R2=88,94 имеет уравнение регрессии y(x1x2x3). Он показывает, что уровень продаж на 88,94

30
зависит от изменения выбранных факторов, остальные 11% - это изменения за счет неучтенных факторов и случайных отклонений.
Проверим значимость полученных уравнений.
Установим сначала общую значимость модели, используя критерий Фишера. Сравним расчетное значение F статистики с табличным F( , 1, 2)
(прил. 4).
- уровень значимости ( =0,05) 1-число степеней свободы числителя
1=m, m-число независимых переменных в уравнении 2-число степеней свободы знаменателя ( 2=n-1-m)
Проверим значимость уравнения Y(x1x2x3) (3.3.1). Расчетное значение критерия F выпишем из табл. 8. (F-Ratio) F=29,49
Из прил. 4 выпишем табличное значение F.
F(0,05, 3, 11)=3,58 |
|
|
=0,05 |
1=3 |
2=11 |
F>F(0,05, 3, 11) |
уравнение регрессии значимо. |
|
Проверим значимость каждого из коэффициентов регрессии. Для |
||
коэффициентов регрессии гипотезы формулируются так: |
||
Н0: вк 0.
Н1: вк 0.
Проведем испытание гипотезы на 5% уровне значимости, пользуясь двусторонним t - критерием при (n-1-m) степенях свободы.
Если t t / 2 , то Н0 отвергается, принимается Н1.
t(0,025, 11)=2,2.
Расчетное значение t статистик выпишем из распечатки (табл. 8,
Tstatistic).
t x |
|
0,71 |
2,2 |
в1 |
3,5 незначим |
1 |
|
|
|
|
|
t x |
2 |
0,65 |
2,2 |
в2 |
незначим |
|
|
|
|
|
|
t x3 |
4,43 |
2,2 |
в3 значим, влияние фактора x3 на моделируемый |
||
показатель можно признать значимым.
Так как два коэффициента регрессии незначимо отличны от 0, то модель не достоверна и не может быть использована для анализа и прогноза показателя Y.
Аналогично проверьте на значимость другие модели.
Значимость уравнения и коэффициентов регрессии можно проверить, используя величину Р.
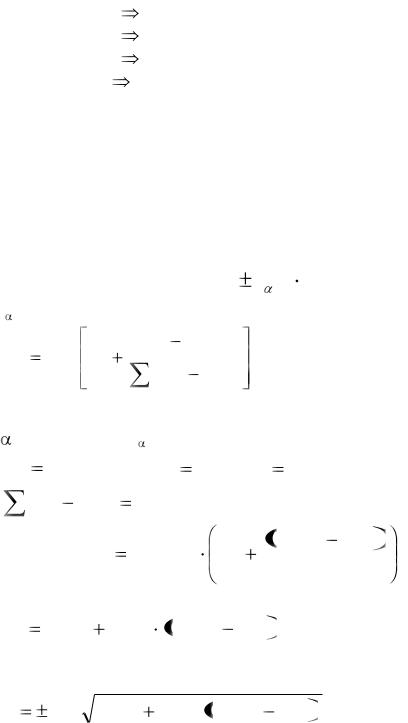
31
В каждой сводке регрессионного анализа рассчитана действительная вероятность появления события Н0 Р-Value. Как уже отмечалось, гипотеза Н0 проверяется на 5% уровне значимости. Если Р-Value меньше 0,05, то Н0 отвергается, следовательно результат является значимым. Если Р-Value больше 0,05, то результат не значим.
Например из табл. 8.
|
P-Value |
|
X1 |
0,4922>0,05 |
в1 – незначим |
X2 |
0,5263>0,05 |
в2 – незначим |
X3 |
0,0010<0,05 |
в3 – значим |
Model |
0,000<0,05 |
уравнение значимо |
3.4.Прогнозные расчеты
Из полученных уравнений регрессии Y(x3) “лучше” описывает изменения объема продаж продукции по выбранному уравнению.
3.4.1. Рассчитаем доверительные границы для уравнения из соотношения.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
yˆ |
|
t |
/ 2 S |
|
|
|
t /2 – статистика Стьюдента. |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x3 р ) 2 |
|
|
|
|
|
|
|||
S y2 |
S |
ост2 |
|
|
|
1 |
|
( x 3 |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
N |
|
( x3i |
|
x3 ) 2 |
|
|
|
|||||||||||||
значение x3 |
для которого определяется yˆ |
|
|
|||||||||||||||||||
=0,05 |
r=15 |
t /2=2,14 |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
S 2 |
(38,01)2 |
|
|
|
||||||||||||
|
x 3 |
105,41 |
|
1444,76 |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
ост |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
(x |
3i |
|
x 3 )2 |
77,82 |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
105,41 x3P |
2 |
|
||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|||||
Получаем S yˆ |
1444,45 |
|
|
|
|
|
|
|
|
. |
||||||||||||
15 |
|
|
77,82 |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
После преобразований получаем. |
|
|
|
|||||||||||||||||||
Sy2ˆ |
96,29 |
16,32 105,41 |
|
x3P |
2 . |
|
|
|||||||||||||||
Следовательно, доверительные границы уравнения регрессии определяются из соотношения
yˆ |
2 |
2,14 96,32 16,32 105,41 x3P |
Графически это будут ветки гиперболы, расположенные выше и ниже прямой линии регрессии, причем гипербола наиболее близко будет
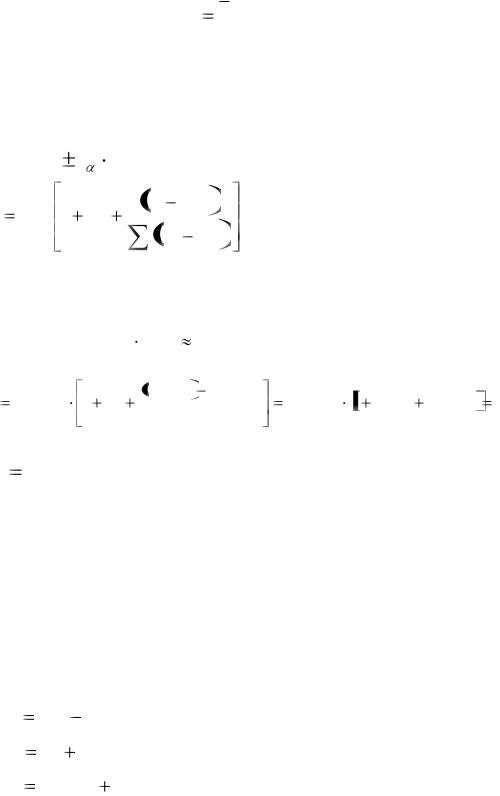
32
располагаться к прямой при x3P x (см. рис. 22). Числовые значения
доверительных интервалов для уравнения получены в табл. 19.
Чтобы получить доверительный интервал для определенных значений, необходимо учесть дисперсию разброса отдельных значений исследуемого показателя вокруг линии регрессии.
Доверительные интервалы для прогнозов индивидуальных значений y
будут равны yˆ |
|
|
|
ˆ |
|
|
|
|
|
|
|
|
|
|
|
||
t SP , |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
ˆ 2 |
2 |
1 |
|
|
|
|
|
x3 |
x3P |
|
|
|
|||||
где SP |
Sост 1 |
|
N |
|
|
|
|
|
|
|
|
|
2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
x2i |
|
x3 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Пусть, например, нужно рассчитать доверительные границы для |
|||||||||||||||||
расчетного значения y |
при x3=105,6. |
|
|
yˆ . |
|||||||||||||
По уравнению регрессии y= - 3796,63+38,87x3 найдем |
|||||||||||||||||
yˆ = - 3796,63+38,87 105,6 |
308,042. |
|
|
||||||||||||||
Вычислим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ˆ 2 |
|
|
|
1 |
|
105,41 105,6) |
2 |
|
|
||||||||
S P |
1444,45 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
1444,45 1 0,666 |
0,0004 1541,22 |
|
15 |
88,514 |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
||||||||||
ˆ
SP 39,25
Доверительные границы
308,042 – 83,99 < y < 308,042+83,99
224,052 < y < 392,032
Доверительные границы прогнозных индивидуальных значений рассчитаем в табл. 19. (Prediction Limits).
Рассчитаем прогнозные значения реализации продукции на ближайшие три полугодия, результаты расчетов поместим в таблице.
Из табл. 15, 16, 17 выпишем уравнения линейных трендов для факторов x1,x2,x3.
x1( x4 ) |
7,2 |
0,02x4 |
|
x2( x |
) |
15 |
0,064x4 |
4 |
|
|
|
x3( x |
) |
102,85 0,32x4 |
|
4 |
|
|
|
Коэффициенты корреляции для этих факторов в зависимости от фактора времени больше 0,7, что говорит о наличии линейных трендов.
33
|
|
|
Таблица 25 |
|
|
|
|
Период |
16 |
17 |
18 |
Прогноз |
|
|
|
Реклама х2 |
6,88 |
6,86 |
6,84 |
Цена ед. прод. |
16,024 |
16,088 |
16,152 |
Индекс |
|
|
|
потребительских |
107,97 |
108,29 |
108,61 |
цен |
|
|
|
y(x3) |
400,163 |
412,6 |
425,04 |
y(x1x3) |
407,71 |
420,79 |
434,107 |
y(x1x2x3) |
399,58 |
412,64 |
425,67 |
y(x1x2) |
322,8 |
330,2 |
337,5 |
Полученные прогнозные значения являются точечными, более обоснованным прогнозом является нахождение интервалов для прогнозных значений.
3.4.5.
Проанализируем основные характеристики объемов продаж с использованием аппарата производственных функций.
Полученные уравнения регрессии можно рассмотреть как производственные функции.
Проведем экономический анализ по фактору х3 – индекс потребительских цен.
y= - 3796,63+38,87 x3
Рассчитаем коэффициент эластичности объема продаж по индексу потребительских цен.
Ex |
|
d y |
: |
y |
|
|
|
||
|
|
|
|
|
|
|
|
||
4 |
d x |
|
x3 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
В начале периода E |
x3 |
30,84 в конце периода E |
11,34. |
||||||
|
|
|
|
|
|
|
|
x3 |
|
E x3 показывает, что d увеличение индекса потребительских цен на 1% увеличивал объем продаж на 30%, а к концу периода на 11,34%.
