Аверянов Введение в оператсионные системы и основы программирования 2015

водная функции f(x) будут определяться выражениями:

На левой границе первая и вторая производная будут иметь вид:

Значения первой и второй производной на правой границе сетки узлов будут вычисляться по формулам:

Задачи по теме «Численное дифференцирование»

Задача 4.20. Вычислить таблицу точных значений первых производных функции ′ на основе аналитических формул дифференцирования и приближенных значений производных по форму-

лам (4.69) – (4.71).

Сравнить результаты.

1.Оценить погрешности (модули разности между точным и приближенным значением).

2.Выяснить влияние на погрешность величины шага h и количества точек N.

251

Варианты функций для задачи 4.20 и 4.21

.

3.sh .

.

6.ch .

7. sh .

9.sh .

10.ch .

11./ .

12.ch .

13.sin .

14.sin .

15.sh .

16.cos .

17.cos .

18.tg π /4 .

19.sin .

20.sin .

22.cos .

23.cos .

24. ln 1 .

25.sin .

26./ .

27. arcsin /2 .

28.arctg .

Задача 4.21. Вычислить таблицу точных значений вторых про-

ренцирования и приближенных значений производных по форму-

лам (4.69) – (4.71).

Сравнить результаты.

1.Оценить погрешности (модули разности между точным и приближенным значением).

2.Выяснить влияние на погрешность величины шага h и количества точек N.

4.6.ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ

4.6.1. Формулы интегрирования, вытекающие из кусочной интерполяции функций

Численное интегрирование – задача вычисления определенного интеграла функции f(x), непрерывной на отрезке [ab]. Если известна первообразная F(x), то определенный интеграл вычисляется по формуле Ньютона–Лейбница:

При трудностях нахождения первообразной функция f(x) может

нить кусочно-линейную интерполяцию функции f(x), заменив ее на отрезках , интерполяционным полиномом Лагранжа первой степени:

. (4.73)

Для увеличения точности интегрирования используется кусоч- но-квадратичная интерполяция функции на отрезке , полиномом Лагранжа второй степени:

, (4.74)

253

и – остаточные члены интегрирования соответствующего прядка точности. В обоих случаях определенный интеграл функции на отрезке [ab] будет равен сумме интегралов на составляющих его отрезках.

Для удобства интегрирования вводится переменная:

. (4.75)

В результате полиномы Лагранжа первой и второй степени запишутся в виде:

Интегрирование полинома Лагранжа первой степени на отрезке [ , сводится к его интегрированию на отрезке [0,1 по переменной q. Новые пределы интегрирования получаются подстановкой старых пределов в выражение (4.75):

Интерполяция функции полиномами Лагранжа второй степени позволяет получить квадратурную формулу Симпсона:

254

(4.80)

1

3 4 .

На отрезке [ локальные интегралы суммируются, при этом количество узлов N должно быть четным:

Численное интегрирование по формулам (4.79) и (4.81) имеет наглядную геометрическую интерпретацию: определенный интеграл – это площадь под кривой функции на отрезке [ .

Кусочно-линейная интерполяция позволяет рассматривать интеграл как сумму площадей локальных трапеций (криволинейных, в случае кусочно-квадратичной интерполяции).

4.6.2. Метод прямоугольников

Существуют еще более простые геометрические интерпретации и соответствующие им методы вычисления определенных интегралов. Это так называемые методы прямоугольников (рис. 4.20 и 4.21). Интегралы вычисляются по формулам (4.82) или (4.83) для ступенчатых функций, которыми интерполируется функция на отрезке [ .

В результате интеграл представляет собой сумму площадей прямоугольников:

(4.82)

или

. (4.83)

255

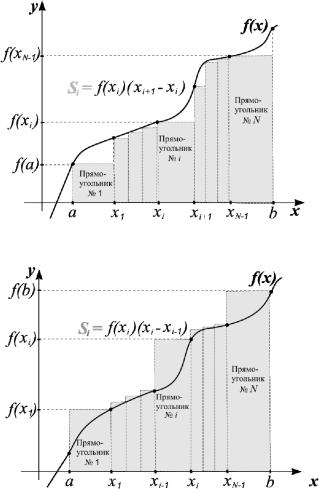
Рис. 4.20. Метод прямоугольников (по нижнемупределу)

Рис. 4.21. Метод прямоугольников (по верхнемупределу)

В первом случае вычисляемая площадь заведомо меньше фактического интеграла, а во втором – заведомо больше, поэтому эти вычислительные схемы называют методами прямоугольников по нижнему и верхнему пределу.

256

вычислительная формула, совпадающая с методом трапеций (4.79).

Задачи по теме «Численное интегрирование»

чины шага h (количества точек N) на расхождение результатов. Для вычисления интеграла используются два метода, указанных

в задаче.

Задача 4.22. Формула прямоугольников и формула трапеций. Задача 4.23. Формула прямоугольников и формула Симпсона. Задача 4.24. Формула трапеций и формула Симпсона.

СПИСОК ЛИТЕРАТУРЫ

1.Таненбаум Э. Современные операционные системы. 3-е изд. СПб.: Питер, 2010.

2.Столяров А.В. Введение в операционные системы: конспект лекций. М.: Издательский отдел факультета ВМиК МГУ им. В.М. Ломоносова, 2006.

3.Иртегов Д.В. Введение в операционные системы. 2-е изд., перераб. и доп. СПб.: БХВ. Петербурr, 2008.

4.Браун П. Введение в операционную систему UNIX: пер. с

англ. М.: Мир, 1987.

5.Колисниченко Д.Н., Аллен Питер В. LINUX: полное руководство. СПб: Наука и техника, 2006.

6.Ктитров С.В., Овсянникова Н.В. Командный язык ОС UNIX: лабораторный практикум. М.: МИФИ, 2007.

7.Уильям Р. Станек Командная строка Microsoft Windows. Справочник администратора: пер. с англ. М.: Издательскоторговый дом «Русская Редакция», 2004.

8.Попов А.В. Командные файлы и сценарии Windows Script Host. СПб.: БХВ-Петербурr, 2002.

9.Баррон Д. Введение в языки программирования: пер. с англ.

М.: Мир, 1980.

10.Роберт У. Себеста. Основные концепции языков программирования: пер. с англ. 5-е изд. М.: Вильямс, 2001.

11.Меткалф М., Рид. Дж. Описание языка программирования Фортран 90: пер. с англ. М.: Мир, 1995.

12.Бартенев О.В. Современный FORTRAN. М.: Диалог-МИФИ,

1999.

13.Программирование на Фортране 77: пер. с англ. / Дж. Ашкрофт, Р. Элдридж, Р. Полсон, Г. Уилсон. М.: Радио и связь, 1990.

14.Ращиков В.И. Численные методы. Компьютерный практикум: учебно-методическое пособие. М.: НИЯУ МИФИ, 2009.

15.Рошаль А.С. Лабораторный практикум по курсу «Численные методы и программирование». М.: МИФИ, 1992.

16.Самарский А.А, Михайлов А.П. Математическое моделирование: Идеи. Методы. Примеры. 2-е изд., испр. М.: Физматлит, 2002.

258