Аверянов Введение в оператсионные системы и основы программирования 2015

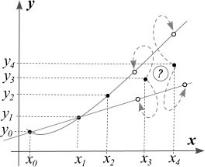
Задача 4.5. Принадлежность точек параболе или прямой. На

,задана также линейная функция. Требуется выяснить, ка-

4.2.ФИГУРЫ НА КООРДИНАТНОЙ ПЛОСКОСТИ

4.2.1.Треугольник на координатной плоскости

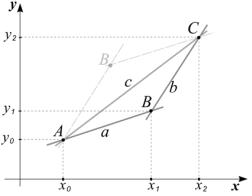
Простейшей фигурой на координатной плоскости является треугольник (рис. 4.8). Если координаты , , и точек A, B и C различны и расположены по возрастанию, то существует всего два вида треугольников: с точкой B выше или ниже прямой AC (как бы ни проводилась сторона AC и какие бы формы или размеры не принимал такой треугольник).

Рис. 4.8. Треугольник на координатной плоскости

Первый закономерный вопрос в отношении треугольника: если отсутствует картинка, но известны длины сторон a, b и c или координаты точек A, B и C – это вопрос о его существовании?

222

Если треугольник определен тремя сторонами a, b и c, то диагональ (максимальная из сторон) может оказаться слишком длинной и две другие стороны просто «не дотянутся» друг до друга, т.е. при трех заданных сторонах длина максимальной из них должна быть строго меньше суммы двух других. Если же длина диагонали равна сумме двух других сторон – это означает что все точки A, B и C лежат на одной прямой?

Точки A, B и C могут оказаться лежащими на одной прямой и в том случае, если треугольник задан координатами этих точек. Это легко проверить, составив уравнение прямой, проходящей через две любые точки, а затем проверить принадлежность оставшейся точки этой прямой.

Убедившись в существовании треугольника можно классифицировать его как тупоугольный, прямоугольный – при наличии в нем таких тупого или прямого угла, а также как остроугольный, если все углы треугольника острые. Классификацию можно построить на теореме косинусов:

где α – угол противолежащий стороне a (аналогичное соотношение можно записать для двух других сторон).

Однако для классификации треугольника можно обойтись следствием теоремы косинусов – теоремой Пифагора. Если сумма квадратов катетов равна квадрату гипотенузы – треугольник прямоугольный, если меньше – треугольник тупоугольный, если больше, тогда остроугольный.

Также можно классифицировать треугольник как равнобедренный при наличии двух равных сторон, а если между собой равны все три стороны – как равносторонний. В противном случае треугольник является разносторонним.

Если треугольник определен точками A, B и C на координатной плоскости (рис. 4.8), то длины его сторон легко находятся по теореме Пифагора:

Рассмотрим задачу нахождения площади треугольника, заданного тремя сторонами или тремя точками. Площадь треугольника при трех известных сторонах a, b и c может быть вычислена по формуле Герона:

Площадь треугольника, заданного точками A, B и C на координатной плоскости (рис. 4.8), может быть также вычислена по формуле Герона (4.16) (после вычисления сторон a, b и c).

В дополнение к вышесказанному рассмотрим геометрический метод вычисления площади треугольника. На рис. 4.8 можно видеть три трапеции: , и , соответственно площадь треугольника будет вычисляться как

Здесь взятие модуля разности гарантирует выполнение этого соотношения для случаев, когда точка B расположена как выше, так и ниже стороны .

Подстановка формул площади трапеции (половина суммы оснований, умноженная на высоту) в (4.17) приводит к формуле

|

(4.18)

|.

4.2.2. Криволинейная трапеция на координатной плоскости

Рассмотрим простейшие методы вычисления площади криволинейной трапеции (рис. 4.9).

Криволинейная трапеция представляет собой область под графиком параболы , ограниченную вертикальными прямыми, проходящими через точки и . Значения коэффициентов a, b и c считаются известными.

224

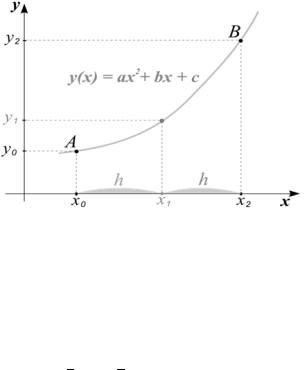
Рис. 4.9. Криволинейная трапеция

Поскольку вычисление первообразной Y(x) от квадратичной функции y(x) не представляет никаких трудностей, то площадь трапеции легко вычислить по формуле Ньютона–Лейбница:

Для контроля правильности полученного результата при программировании задачи вычислим с использованием интерполяционного полинома Лагранжа второй степени (4.11). Для этого

принимающую целые значения 0, 1 и 2 в точках , и . Тогда с учетом (4.20) и (4.21) выражение для интерполяционного полинома Лагранжа второй степени (4.11) запишется как

1 2 2 1 . (4.22)

Интегрируя полином Лагранжа в соответствующих пределах, получим выражение

(4.23)

4,

называемое формулой Симпсона.

Задачи по теме «Фигуры на координатной плоскости»

Задача 4.6. Существование и классификация треугольника, определённого через длины сторон. Задано несколько троек чи-

сел a, b и c – возможные стороны треугольника (см. варианты заданий). Необходимо выполнить следующие действия.

1.Запрограммировать последовательный ввод с клавиатуры значений a, b и c.

2.Переставить значения длин сторон a, b и c таким образом, чтобы сторона c оказалась гипотенузой.

3.Проверить возможность существования треугольника с гипотенузой в соответствии с теоремой косинусов (используя формулу (4.14)) или теоремой Пифагора.

4.Если треугольник существует, то на основании теоремы косинусов или теоремы Пифагора классифицировать его как:

1) тупоугольный;

2) прямоугольный;

3) остроугольный.

226

5. Классифицировать существующий треугольник как:

1)разносторонний;

2)равносторонний;

3)равнобедренный.

Варианты данных для задачи 4.6

Задача 4.7. Существование и классификация треугольника, определённого через координаты вершин на плоскости. На ко-

ординатной плоскости задано несколько наборов по три точки A, B и C с координатами , , , и , соответственно

(см. рис. 4.8).

1.Необходимо проверить существование треугольника (не лежат ли точки на одной прямой).

2.Если треугольник существует, то классифицировать его как тупоугольный, прямоугольный или остроугольный, а также как разносторонний, равнобедренный или равносторонний.

Задача 4.8. Вычисление площади треугольника, определённого через координаты вершин на плоскости. Дополнить задачу

3.7 (используя те же варианты данных) вычислением площади треугольников по формуле Герона, а также через суперпозицию площадей трапеций. Сравнить результаты. Погрешность вычислений:

ε0,01.

Задача 3.9. Вычисление площади криволинейной трапеции.

Вычислить площадь криволинейной трапеции (см. рис. 4.9) по формуле Ньютона–Лейбница (4.19) и проверить результат по формуле Симпсона (4.23). Трапеция ограничена параболой

Варианты данных к задаче 3.9

1. 7,54; 6,34; 4,52; 1,19; 3,02.

228

4.3. РЕШЕНИЕ НЕЛИНЕЙНЫХ УРАВНЕНИЙ

4.3.1. Подход к решению нелинейных уравнений

Распространенной задачей в самых разных областях вычисле-

Рис. 4.10. Приближенное решение нелинейного уравнения. Пологая функция

229

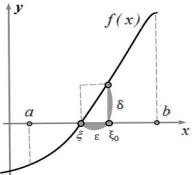
Рис. 4.11. Приближенное решение нелинейного уравнения. Крутая функция

При этом значения функции в точках ξ и ξ должны отличаться не более чем на величину невязки δ – малой положительной величины. Величины погрешности и невязки являются необходимыми начальными данными для решения задачи нахождения корня нелинейного уравнения:

Значимость величин отклонения – погрешности ε и невязки δ, иллюстрируется на рисунках выше. Если в окрестности корня ξ функция достаточно пологая (см. рис. 4.10), то величина погрешности ε достаточна для регулирования точности решения. Если же функция круто возрастает или убывает (см. рис. 4.11), то для точности решения становится существенным значение невязки δ.

4.3.2. Деление отрезка пополам (дихотомия)

Основная идея решения уравнения (4.24) методом дихотомии заключается в том, что корень уравнения – ξ, являющийся внутрен-