Леонтева Сборник лабораторныкх работ по физике Мекханика 2015

Образец представляет собой прямоугольную пластинку, выполненную из различных материалов. Каждый образец имеет две рабочие поверхности с разной чистотой обработки.

В верхнем кронштейне 7 размещается механизм подвеса маятника, который позволяет регулировать его длину.

Маятник 8 представляет собой тонкую эластичную нить с подвешенным на ней испытуемым шаром, который в свою очередь, имеет конус, предназначенный для пересечения оптической оси датчика фотоэлектрического 9.

Датчик фотоэлектрический 9 размещается на нижнем кронштейне и служит для выдачи электрического сигнала на миллисекундомер 10.

Миллисекундомер физический 10 выполнен самостоятельным прибором с цифровой индикацией времени и количества полных периодов колебаний маятника. Миллисекундомер жестко закреплен на основании и соединён кабелем с датчиком фотоэлектрическим. Устройство и принцип работы миллисекундомера приведены в паспорте ФПМ 14 ПС.

Меры безопасности

К работе с установкой допускаются лица, ознакомленные с её устройством и принципом действия

Перед началом работы с установкой убедитесь, что она заземлена. Во избежание поломки червячного редуктора не разрешается прилагать дополнительных усилий к верхнему кронштейну и вертикальному стержню.

После проведения работы с установкой необходимо отключить миллисекундомер от сети.

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

1. Подготовьте установку к работе. Для этого:

-установите в гнездо шкалы исследуемый образец;

-отрегулируйте положения основания при помощи регулировочных опор таким образом, чтобы нить подвеса маятника совпала

снулевым делением шкалы;

-установите с помощью маховичка угол наклона образца рав-

ным 90°, при этом шарик должен касаться поверхности исследуе-

81

мого образца, а сила нормального давления должна отсутствовать. Добейтесь этого с помощью регулировочных опор;

-установите угол наклона образца равным 6°. Отрегулируйте длину маятника с помощью устройства на верхнем кронштейне таким образом, чтобы при колебании маятника шарик перемещался по рабочей поверхности образца, не касаясь шкалы;

-подключите к разъёму ВХОД на миллисекундомере фотоэлектрический датчик. Включите в сеть шнур питания миллисекундомера;

-нажмите на кнопку СЕТЬ, расположенную на лицевой панели миллисекундомера, при этом должны загореться цифровые индикаторы;

-отклоните рукой маятник на угол 5–6°, нажмите кнопку СБРОС на лицевой панели миллисекундомера и без толчка отпустите маятник. Убедитесь, что маятник совершает колебательные движения и миллисекундомер отсчитывает время и число полных колебаний маятника;

-после 15–20 колебаний маятника нажмите на кнопку СТОП миллисекундомера, при этом убедитесь, что счёт времени и числа полных периодов колебаний прекращается в момент очередного периода колебаний.

2.Протрите рабочие поверхности исследуемых образцов неворсистой тканью, смоченной в спирте (бензине).

3.Запишите в табл. 10.1 материал шара маятника и исследуемого образца.

4. Установите угол наклона образца β = 30°.

82

5.Отклоните маятник от положения равновесия на угол α0 ~ 10°, нажмите кнопку ПУСК и отпустите маятник.

6.Нажмите кнопку СТОП миллисекундомера при достижении

амплитуды колебания маятника αn ~ 5°, снимите с миллисекундомера число n полных колебаний маятника. Запишите значения углов α0, αn и число колебаний п в табл. 10.1.

7.Аналогичные измерения проведите для углов наклона образ-

ца β = 45°, β = 60°, β = 75°.

8.Вычислите коэффициент трения k по формуле (10.3) для каждого угла наклона и результаты запишите в табл. 10.1.

9.Найдите погрешность измерения k и запишите её в табл.

10.1.

10.Повторите измерения для всех пар образцов, входящих в установку.

11.Если значения k для всех углов наклона β имеют близкие значения, значит все предположения при выводе расчётной формулы (10.3) верны. Если значения k имеют значительный разброс, следовательно какие-то из предположений в данном опыте не выполняются. Какие именно предположения не выполняются в вашем опыте?

КОНТРОЛЬНЫЕ ВОПРОСЫ

1.Какие виды движения может совершать твёрдое тело?

2.Сформулируйте теорему Эйлера.

3.Что называется моментом силы?

4.При каких условиях возникает вращение твёрдого тела?

5.Чем определяется угловое ускорение твёрдого тела?

6.Что называется трением качения?

7.Что такое коэффициент трения качения?

8. Выведите формулу k = R tg β cos αn −cos α0 .

2n(αn + α0 )

9. Почему автомобили, предназначенные для езды по бездорожью, снабжены колёсами большого диаметра?

83

Приложение к работе 10

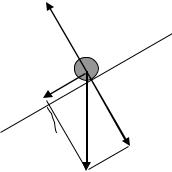
Для вывода формулы (10.3) воспользуемся законом сохранения энергии:

Выберем в качестве точки 1 ту, где маятник отклонён на максимальный угол α0. При этом его скорость равна нулю и Е1 = U1, где U1 – потенциальная энергия шарика в точке 1.

Аналогично, точка 2 – это положение максимально отклонённого маятника, совершившего n колебаний. Точно также Е2 = U2, где U2, потенциальная энергия в точке 2. Итак:

Е2 − E1 = U2 − U1.

В (10.П2) первые два члена справа представляют собой работу силы трения покоя, а последний член – работу трения качения. Поскольку по определению коэффициента трения качения Fтр = kN/R, то два последних слагаемых взаимно уничтожаются, и работа силы трения:

dAтр = −FтрdS .

где Sn – путь, пройденный шариком за n колебаний

Найдём теперь Sn. Если шарик совершил одно колебание, то он прошёл путь равный

L(α0 + α' + α' + α1), (10.П3)

где α0 − начальный угол отклонения, α1 – конечный угол отклонения, α' – максимальный угол отклонения после прохождения шари-

84

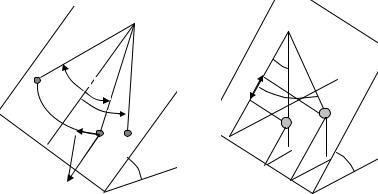
ком положения равновесия (рис. 10.П2). Так как трение качения мало, то изменение амплитуды за одно колебание также мало:

α0 ≈ α' ≈ α1.

Поэтому путь, пройденный за одно колебание, можно записать как 2L(α0 + α1). Аналогично, путь, пройденный за второе колебание

2L(α1 + α2). Путь, пройденный за n-е колебание – 2L(αn–1 + αn). Сумма этих величин и есть Sn:

Sn = 2L(α0 + α1) + 2L(α1 + α2) +...+ 2L(αn-1 + αn).

Найдём убыль потенциальной энергии шарика за одно колебание с произвольным номером m:

Um−1 – U m = mg (hm−1 – hm),

где hm−1 и hm – значения высоты, на которой находится шарик в

С другой стороны, эта величина равна работе сил трения за одно колебание:

Um−1 – U m = Aтр = Fтр Sm = 2k NL(αm–1 + αm)/R. (10.П5)

85

Поскольку углы отклонения малы, то:

Таким образом, при каждом колебании угол отклонения уменьшается на одну и ту же малую величину

Δα = 4Rk ctgβ.

Тогда углы α0 , α1 , α2 ,... образуют арифметическую прогрессию и

Sn = 2n·L· [(α0+ α1) + (αn-1+ αn)]/2 ~ 2 ·n·L· (α0+αn).

Найдём теперь из (10.П4) убыль потенциальной энергии шарика за n колебаний:

U0 – Un = m·g·L· (cos αn – cos α0)·sin β.

Приравнивая её работе сил трения за n колебаний:

Aтр = Fтр Sn = k·N·2· n· L· (α0+αn)/R, (10.П8)

после сокращения на m·g·L, с учётом малости всех углов отклонения, получаем формулу для коэффициента трения качения k:

k = R α0 −αn tgβ. 4n

Оценим теперь условия, при которых справедливы полученные результаты. Мы предполагали, что затухание колебаний является слабым, поэтому количество колебаний п велико:

86

Это неравенство означает, что все наши выводы справедливы, если угол наклона β не слишком мал, причём это требование тем существенней, чем больше k. В условиях данной лабораторной работы максимальный угол отклонения α0 ~ 10°~ 1/6 рад, k ~ 5 10–3 см, R~ 1 см. Тем самым

Наличие сильного неравенства означает, что tgβ, по крайней мере, в 3–4 раза больше 0,12. Таким образом, tgβ ≥ 0,5, поэтому

β ≥ 30°.

На величину угла β накладывается также ограничение сверху, т.е. угол β не может быть слишком большим. Действительно, если угол β окажется очень близким к 90°, то шарик будет слабо прижиматься к наклонной плоскости, сила реакции N = m·g·cosβ будет мала, а вместе с ней и сила трения также будет мала. Но при такой слабой силе трения шарик будет скользить по поверхности. Найдём максимально допустимый угол наклона поверхности. Он определя-

ется из условия Fтр.пок < kскольжN. Сила реакции опоры N = mg·cosβ, а проекция силы тяжести на направление движения шарика равна

(см. рис. 10.П2)

mg sinβ sinα.

Сила трения покоя не может быть больше этой величины, откуда получаем неравенство

mg sinβ sinα<kскольжmg·cosβ.

Сокращая обе стороны на mg, находим

tgβ < kскольж/sinα0.

Коэффициент трения металлов имеет величину близкую к 0,7, угол α0 ~ 1/6, откуда получаем

tgβ < 4.

Это неравенство даёт ограничение:

β < 75°.

Итак, угол наклона β должен находиться в диапазоне: 30°< β < 75°.

87

Работа № 11

ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ И ПРОВЕРКА ТЕОРЕМЫ ШТЕЙНЕРА МЕТОДОМ КРУТИЛЬНЫХ КОЛЕБАНИЙ

Цель работы: определить момент инерции цилиндра относительно оси, проходящей через центр тяжести тела, и проверить теорему Штейнера.

Приборы и принадлежности: трифилярный подвес, образцы для измерения (цилиндры), секундомер, штангенциркуль.

ВВЕДЕНИЕ

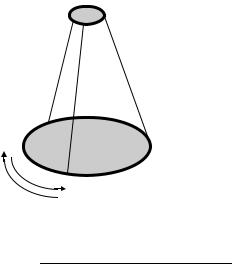
В данной работе определяется момент инерции тела и проверяется на опыте справедливость теоремы Штейнера. Для этой цели используется метод крутильных колебаний, применяемый на приборе с трифилярным подвесом, представляющим собой круглую платформу, подвешенную на трёх симметрично расположенных нитях, укреплённых у краёв платформы (рис. 11.1).

1 Вывод формулы (11.1) см. в приложении 2.

88

где L – длина нити, m – масса системы (платформы или платформы с грузом), R – радиус нижней платформы, r – радиус верхнего диска, I – момент инерции системы. На использовании этой зависимости и основана методика нашей работы.

Из формулы (11.1) получаем выражение для момента инерции платформы

Это соотношение справедливо, если погрешности измерения остальных величин L, m, R, r малы.

Для того чтобы определить момент инерции Iц цилиндра относительно оси, проходящей через его центр тяжести, следует определить момент инерции пустой платформы I0 и момент инерции I1 платформы, нагруженной цилиндром, расположенным посередине платформы. В этом случае ось вращения проходит через центры тяжести платформы и цилиндра. Очевидно, что I1 = I 0 + Iц, откуда

В лабораторной работе проверяется также справедливость теоремы Штейнера, согласно которой момент инерции тела I относительно любой оси ОО' равен сумме момента инерции этого тела Iц относительно оси CC', параллельной данной и проходящей через центр тяжести тела, и произведения массы тела m на квадрат расстояния d от центра тяжести тела до оси

вращения (рис. 11.2):

I = Iц + md2.

Для проверки этой теоремы необходимо измерить величины Iц и I, а также измерить расстояние d и массу тела m. После этого сравнить величину I – Iц с величиной md2.

89

Величина Iц определяется в первой части работы. Для проверки теоремы Штейнера следует поместить симметрично относительно оси вращения по краям платформы два одинаковых цилиндра (рис. 11.3) и определить момент инерции платформы I2, нагруженной этими цилиндрами.

будет моментом инерции одного цилиндра относительно оси, отстоящей от его центра

dтяжести на расстоянии d. Затем, измерив расстояние d, следует проверить, будет ли величина I – Iц равна величине md2.

3. Измерьте период колебаний T0 ненагруженной платформы. Для этого сообщите нижней платформе вращательный импульс резким поворотом верхнего диска так, чтобы нижняя платформа повернулась на 6–8 градусов, Измерьте t0 – время 30 полных колебаний, и вычислите T0 = t0 /30.

90