Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный исследовательский ядерный университет (МИФИ)

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Баскаков Несобственные интегралы 2014

.pdf

Скачиваний:

Добавлен:

12.11.2022

Размер:

1.05 Mб

Скачать

☆

<<< < Предыдущая 1 2 34 / 64 5 6 > Следующая >>>

−1

1−r

e− y dy

(1 −e

)∫

−i ∫

+ ∫

+o(1) = 0 ,

(7.10)

πiy

−1

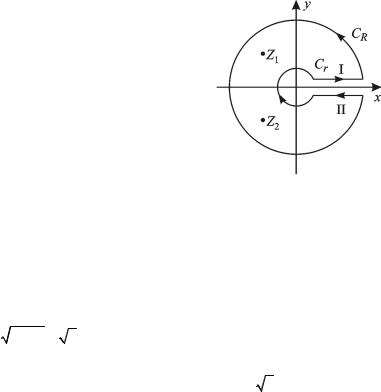
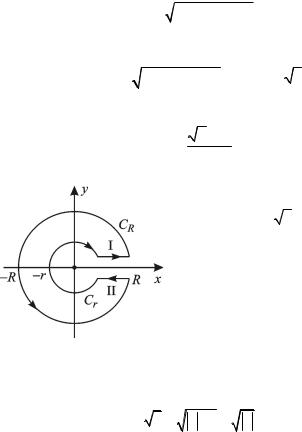
где I, II – дуги окружности, получающиеся при обходе особых то-

чек z = i , z = 0 соответственно.

Вблизи точки z = i

имеем:

eiz

e−1 +c (z −i) +...

e−1

f (z) = e2π( z−i) −1 =

2π(z

−i) +c2′

(z −i)2

+... =

2π(z −i) + p(z −i) ,

где p(z −i)

– правильная функция в точке z = i . Поскольку на дуге

I имеем z =i +reiϕ ,

dz = ireiϕdϕ, то

∫

e−1

−π∫/2

ireiϕ dϕ

+ o(1) = −ie−1 / 4 + o(1) , r → 0 .

2π

iϕ

Аналогично,

∫

∫0

i dϕ+ o(1) = −

+o(1) ,

r → 0

2π

π/2

и равенство (7.10) принимает вид

−1

1−r

e−y

−1

(1 −e

)∫

= i ∫

dy +

(1 + e

) + o(1)

(7.11)

2πiy

−1

при r → 0 ,

R → ∞.

Отметим, что

1−r

e− y dy

1−r

e−y

−1

∫

= − ∫

dy =

−1)

+ o(1) ,

(7.12)

2πiy

−

тогда отделяя в (7.11) мнимую и действительную часть, пользуясь выражением (7.12), окончательно получаем:

∞	sin x			1		1	−1
∫e−πx		dx =					+ e	−1 .
			2				−1
0	sh πx				1		−e
Пример 7.6.* Вычислить интегралы Эйлера
J1 = +∞∫cos x2 dx ;			J2		= +∞∫sin x2 dx .
0							0

В качестве вспомогательной функции выбираем f (z) = eiz2 , а контур подсчета интегралов указан на рис. 7.9.

Рис. 7.9

Контур C =[0; R] CR [BO] . На дуге CR после замены ξ = z2 получим

	∫	f (z) dz =	1	∫ eiξ dξ		,
	CR		2	C′2	ξ
				R
где C′	2 – четверть окружности радиуса				R2	. Тогда по лемме Жор-
R

дана этот интеграл стремится к нулю при R → ∞.

По теореме Коши, если на OA положить z = x , а на OB z =± i , имеем:

∫R eix2 dx + ∫+ i ∫0 e−t2 dt = 0 .

0 CR R

Переходя к пределу при R → ∞ и пользуясь значением интеграла вероятности erf∞ =1 , получим:

+∞∫eix2 dx = i	π	.
	2
0

Отделив в этом выражении действительную и мнимую часть, получаем:

+∞∫cos x2dx =	+∞∫sin x2dx =	1	π .	(7.13)

0	0	2	2

С последними интегралами связаны специальные функции – интегралы Френеля:

S (x) = ∫x	sin t dt	;	C(x) = ∫x	cost dt	.

0	2πt		0	2πt

Действительно, их можно легко получить из (7.13) с помощью замены t = τ2 . Пользуясь этой подстановкой, получим:

	2	x
S(x) =	2	∫sin τ2dτ,
S(x) =	π	∫sin τ2dτ,
		0
	2	x
C(x) =	2	∫cos τ2dτ.
C(x) =	π	∫cos τ2dτ.
		0

Тогда выражение (7.13) можно записать в виде

S(+∞) =C(+∞) =1/ 2 .

8. ВЫЧИСЛЕНИЕ ИНТЕГРАЛОВ, СОДЕРЖАЩИХ МНОГОЗНАЧНЫЕ ФУНКЦИИ

В этом разделе рассмотрим примеры вычисления интегралов, содержащих многозначные функции в составе подынтегральной.

Пример 8.1. Вычислить интеграл

			+∞	ln x dx
			∫					.
			∫	(x	2	+1)	2	.
			0	(x		+1)
В	качестве		вспомогательной						рассмотрим	функцию
f (z) =	ln z	, имеющую особую точку при z = 0 (точка ветвле-
f (z) =	(z2 +1)2	, имеющую особую точку при z = 0 (точка ветвле-
	(z2 +1)2
ния функции ln z ).
Тогда воспользуемся контуром, в котором для f (z)										возможно
выделение однозначной ветви (рис. 8.1).

Рис. 8.1

Обозначим через ln z ту часть, которая определяется равенством 0 < arg z < π. Тогда f (z) в точке z = i имеет полюс второго

порядка с вычетом

c−1	= lim	d	(z −

	z→i	dz

По теореме о вычетах

	−r
	∫	+ ∫
	−R	Cr

i)2 f (z)		=	d	ln z				=	π+ 2i .

			dz	(z +i)2				z=i	8

+ ∫R	+ ∫		dz =		iπ2	−		π .

r		CR		4			2

При z = R eiϕ , 0 < ϕ< π имеем, начиная с достаточно большого R,

ln z = ln2 R +ϕ2 ≤ 2ln R ;

следовательно,

	∫		≤		2ln R	πR
	∫		≤		2 2	πR
	СR				(R −1)
и ∫→0 при R → ∞.
CR
Аналогично получаем,		что при z = reiϕ , 0 < ϕ< π, начиная с
достаточно малого r,
		ln z		≤ 2ln1 / r ,
		ln z		≤ 2ln1 / r ,

следовательно,

∫≤ (12ln1− r2/)r2 πr

и этот интеграл также стремится к нулю при r → 0 . Преобразуя с помощью замены z = −x первый интеграл, получим:

−r	R	ln x +iπ
∫	= ∫					dx .
		(1+ x	2	)	2
−R	r

Таким образом, в пределе при r → 0 , R → ∞ получаем:

2 +∞∫	ln x dx	+πi +∞∫	dx			=	iπ2	−	π .
	2 2		2	)	2
0	(1 + x )	0	(1+ x			4			2

Сравнивая действительные и мнимые части, получаем:

+∞

ln x dx

∫

; ∫

= −

+1)

Пример 8.2.* Вычислить интеграл

+∞	ln x dx
∫0
		.
	(x +1)2 + 4

Для вычисления данного интеграла воспользуемся вспомогательной функцией

f (z) =	ln2	z
	(z +1)2		+4

и контуром, указанным на рис. 8.2.

Контур выбран таким образом, чтобы f (z) была однозначна на нем,

т.е. внутри контура ln z однозначен, так как считаем, что 0 < arg z < 2π . На

верхнем и нижнем берегах разреза, входящего в контур, ln2 z принимает значения ln2 x и

(ln x + 2πi)2 = ln2 x + 4πiln x −4π2

соответственно. Тогда интегралы от

ln2 x взаимно уничтожаются и появляется возможность вычислить искомый интеграл. Внутри контура лежат

два	полюса	z1,2 = −1±2i функции
f (z)	с вычетами
			(c		)	=	1		[ln r +i(π−ϕ)]2 ,
			(c		)	=			[ln r +i(π−ϕ)]2 ,
			−1 1				4i
							4i
			(c	)		= −		1		[ln r +i(π+ϕ)]2 ,
			(c	)	2	= −				[ln r +i(π+ϕ)]2 ,
			−1		2			4i
								4i
где r = 1 + 22		=	5 ; ϕ = arctg 2 .
Применив теорему о вычетах, получаем
		∫ + ∫ + ∫ + ∫ = π2 4ϕ(π−i ln
		I	II	CR				Cr

Рис. 8.2

5 ).

В соответствии со сказанным выше имеем:

4πi ln x − 4π2

∫

+ ∫ = −∫

dx .

(x +

+ 4

Как

предыдущем

примере,

следует доказать, что

limr→0

∫= Rlim→∞

∫=0 , и тогда в пределе при

r → 0 ,

R → ∞ получаем,

что

+∞

ln x dx

4πϕ

(π−i ln 5 ).

4π

∫0

− 4πi ∫0

(x +1)2 + 4

Сравнив мнимые части, получим искомый интеграл

+∞

ln x dx

ϕln

∫0

arctg 2 .

(x +1)2 + 4

Пример 8.3.* Вычислить интеграл

+∞

x−1/ 2

∫0

dx .

x +1

Этот интеграл можно вычислить двумя способами.

Способ 1. Сделаем сразу подстановку x =et , тогда данный интеграл сводится к интегралу, аналогичному интегралу в примере

7.4 из разд. 7.

Способ 2. В качестве вспомогательной рассмотрим функцию


f (z) =		z−1/ 2		=	e−1/ 2 ln z	,
	1		+ z		1 + z

а в качестве контура возьмем контур на рис. 8.3.

Заметим, что на нижнем берегу разреза

		1	πi
	2

Рис. 8.3	f (xe2πi ) =e	2	f (x) .

Проделав все основные выкладки и оценки получили:

+∞∫	x−1/ 2 dx	=	π	= π.
	1 + x		sin π / 2
0

Пример 8.4. Вычислить интеграл

2∫π	dt		.
		2
0 (2 + cost)
Интегралы этого типа легко	вычисляются с помощью замены
z = eit . Тогда

dt = dz / ieit = dz / iz ;

cost = 12 (z +1/ z) .

Исходный интеграл представим в виде:

2∫π

∫

z dz

0 (2 + cost)

+ 4z +1)

Внутри окружности

=1 подынтегральная функция имеет один

полюс z0 = 3 − 2

c−1

с вычетом

	z			1
d					.
=			=
	3 + 2))2			2 33/ 2
dz (z + (
		z=z0

По теореме о вычетах искомый интеграл равен

2∫π	dt		=	4π	.
2∫π	(2 + cost)	2	=	3/2	.
0	(2 + cost)			3

Пример 8.5. Вычислить интеграл

2∫π	(1+ 2cost)2 cos 2t	dt .
	5 / 6 −1 / 3cos t
0

Решение осуществляется с помощью замены z = eit . Тогда имеем:

2∫π

(1 + 2cost)2 cos 2t dt

∫

(1+ z + z2 )2 dz

5 / 6 −1/ 3cost

z −

(1 + z2 )

Один из корней подынтегральной функции

z = 5 / 6 ±		7 / 12
1,2	1	/ 3

лежит внутри, а другой – вне окружности z =1, так как z1z2 =1;

причем эти корни – действительные и различны. Тогда по теореме о вычетах

	2π		(1+ 2cost)2 e2it dt					(1+ z		+ z2 )2			2π					z	2
	∫						= 2π		1	1	=							1	,
	∫		5	/ 6 −1/ 3cost			= 2π	5 / 6 − z / 3			=						1/ 6		,
	0									1			7 /12
где z1			1	5			5		1			z1		5		3		7
	=				−	7 /12	=3	−		7 / 13	,		=	2	−				– полюс,
	=	1/ 3			−	7 /12	=3	−	2	7 / 13	,		=		−	2		3	– полюс,
		1/ 3		6			6		2							2		3

лежащий внутри окружности. Откуда, пользуясь действительностью правой части последнего равенства, получаем:

2π	(1	+ 2cost)				2	cos2t				2π					5		1	2
∫	(1	+ 2cost)					cos2t		dt =		2π					5	−	1			.
		5		1									18
										7 / 12			18			6		12
										7 / 12						6		12
0			−		cost
0		6	−	3	cost
		6		3
Пример 8.6.* Вычислить интеграл
							1			dx
							∫			dx				.
							∫	3 (1− x)(1 + x)				2		.
							−1	3 (1− x)(1 + x)
В качестве вспомогательной рассмотрим функцию																				g(z) =		1	,
В качестве вспомогательной рассмотрим функцию																				g(z) =		f (z)	,
																						f (z)
где f (z) = 3 (1− z)(1+ z)2 .								Функция f (z)							во внешности отрезка

[−1;1] распадается на три однозначные ветви. Действительно, положим ϕ1 = arg(1 + z) ; ϕ2 =arg(1− z) . При обходе против часовой стрелки замкнутого пути, изображенного на рис. 8.4 пунктиром,

каждый	из ϕ1	и ϕ2 получает приращение		2π , но тогда
arg f (z) =	ϕ1 + 2ϕ2	получает приращение	2π и,	таким образом,
	3
f (z) возвращается к исходному значению.
Будем рассматривать ту ветвь функции			f (z) ,	которая на верх-

нем берегу отрезка [−1;1] принимает положительное значение. Возьмем контур, который на рис. 8.4 изображен сплошной ли-

нией. На берегу I имеем arg f (z) = 0 , т.е. f (z) = 3 (1 − x)(1+ x)2 ; на

берегу II, после обхода точки z =1 по часовой стрелке, arg f (z) = −2π/ 3 , т.е. f (z) = e−2πi /3 3 (1− x)(1+ x)2 .

Рис. 8.4

Оценивая аналогичным способом, изложенным выше, интегралы по малым окружностям Cr′, Cr′′, получаем, что они стремятся к

нулю при r → 0 . Далее, по теореме Коши для многосвязных областей:

(1 −e2πi/3 ) ∫1	dx		= ∫	dx	.
		2		f (x)
−1 3 (1− x)(1 + x)			CR
Остается вычислить ∫,	для чего воспользуемся разложением
СК

выбранной ветви в окрестности бесконечно удаленной точки. Для этого выносим ( −z3 ) из-под знака корня и преобразуем выражение

g(z) =

−

1 −1/3

−2/3

f (z)

−πi/3

где

−

1 −1/3

1 −2/3

– те ветви функций,

которые положи-

тельны на сегменте (1; R) при достаточно больших R действительной оси. Разложим последние по формуле бинома, находим вычет

выбранной ветви в бесконечно удаленной точке. Этот вычет равен

(−eπi/3 ) – коэффициент при

1 / z

с обратным знаком. Пользуясь

тем, что ∫ равен произведению 2πi

на этот вычет, получаем

(1 −e2πi/3 ) ∫1

= −eπi/3 2πi ,

3 (1 − x)(1 + x)

−1

откуда

2π

∫

3 (1− x)(1 + x)

sin

−1

Пример 8.7.* Вычислить интеграл

+∞∫

Рис. 8.5

4 z = 4

4x ln x dx .

x2 +9

Для вычисления интеграла в качестве вспомогательной возьмем функ-

цию f (z) =	4	z ln z	, имеющую точ-
	z	2 +9

кой ветвления		z = 0 , и контур, в ко-

тором многозначная функция f (z)

распадается на ветви (рис. 8.5). Выбираем какую-либо ветвь функции

f (z)	в		указанном	контуре:
ln z = ln	z	+i(ϕ+ 2πk) ,		положив,

например,			k = 0 ,	получаем
ln z = ln	z		+iϕ,

z eiϕ = 4 z eiϕ/ 4 .

Очевидно, что на верхнем берегу разреза, обозначенном I на

рис. 8.5, z = xei0 = x , а на нижнем берегу (II) – z = xe2 πi .

В данном контуре однозначная функция имеет полюсы первого порядка z1,2 = ±3i . Тогда, пользуясь теоремами Коши, имеем:

<<< < Предыдущая 1 2 34 / 64 5 6 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
12.11.20221.02 Mб1Банкова НумералсНумберс Анд Фигурес ин Профессионал 2011.pdf
#
12.11.2022738.59 Кб4Банкова ПРАЦТИЦЕ МАКЕС ПЕРФЕЦТ ПРЕСЕНТ ФОРМС 2015.pdf
#
12.11.20221.91 Mб43Баранник Лекции по курсу Теория переноса нейтронов 2012.pdf
#
12.11.20221.09 Mб4Баранов Лабораторный практикум 2012.pdf
#
12.11.2022508.05 Кб7Барменков Дополнителные главы курса ТФКП.Римановы поверкхности 2015.pdf
#
12.11.20221.05 Mб5Баскаков Несобственные интегралы 2014.pdf
#
12.11.20223.67 Mб0Батова Бридгинг тхе Гап 2013.pdf
#
12.11.20222.38 Mб1Бежко Применение ЕВМ в експерименталных исследованиях 2011.pdf
#
12.11.20221.81 Mб0Белехов Психолого-педагогическое обеспечение образоватлного 2011.pdf
#
12.11.2022583.9 Кб3Белобородов Надежност тестов 2012.pdf
#
12.11.20224.94 Mб60Беляев Физика ядерной медицины Ч.2 Учебное пособие 2012.pdf