Баскаков Несобственные интегралы 2014

∫b

f (x) dx + ∫ f (z) dz = 2πiK ,

(7.1)

a

C

Таким образом, вопрос

вычисления интеграла по ин-

тегралу (a; b) сводится к вы-

числению интеграла по кон-

туру C с помощью формулы

(7.1).

Если интервал (a; b) сов-

Рис. 7.1

падает с (−∞; +∞) , и функция

∫R

f (x) dx + ∫ f (z) dz = 2πi KR .

(7.2)

−R

CR

Заметим, что при

R → ∞ интеграл ∫R

f (x) dx

стремится к ис-

−R

Условия, о которых мы здесь упомянули, вытекают из следую-

щих лемм.

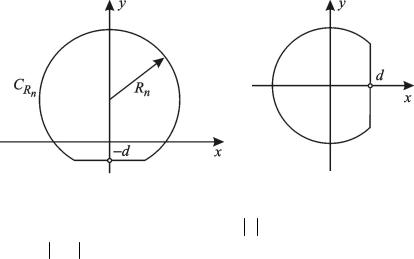
Лемма 7.1 (Жордана). Пусть d – некоторое положительное чис-

ло;

{R }∞

– последовательность положительных чисел,

R → ∞;

n n=1

функция

g(z) имеет лишь

конечное число особых

точек, а

CR

={z :

z

= Rn , Im z > −d} (рис. 7.2). Тогда если

n

lim sup g(z) = 0 , то lim

∫

g(z)eiλz dz = 0

n→∞ z CR

n→∞

n

CRn

форме: в условиях леммы из равенства lim sup g(z) = 0 следует

R→∞ z CR

Rlim→∞

∫ g(z)eiλz dz = 0 .

(7.3)

CR

Rlim→∞ ∫g( p)epλ dp =0 .

(7.4)

γR

Если сделать замену p = −p ,

то получаем следующую формули-

ровку леммы Жордана.

Лемма 7.1′′. Пусть d ≥ 0 и γR ={z :

z

= R, Re z ≥ −d}

(рис. 7.3).

Тогда если lim sup

g(z)

= 0 , то для любого λ < 0

R→∞ z γR

Rlim→∞ ∫g( p)epλdp =0 .

R

γR

}

Пусть C

={z :

z

= R, Im z ≥

0 .

а ее аналитическое продолжение

f (z)

имеет лишь конечное число

особых точек {μ

}n

в области Im z > 0 и, крометого,

K

k =1

Rlim→∞ ∫

f (z) dz = 0 .

(7.5)

Тогда

CR

+∞

f (x) dx = 2πi

n

Res f (z) .

∫

∑ z=μk

−∞

k =1

Если функция

f (x)

определена на (−∞; +∞) всюду,

за исклю-

чением точек x1 , x2 , …,

xl , то для вычисления интеграла

+∞

x1 −ρ

(V .P.) ∫

f (x) dx = Rlim→∞

limρ→0 ∫

f (x) dx +

−∞

−R

x2 −ρ

xl −ρ

R

+ ∫ f (x) dx +... +

∫

f (x) dx + ∫

f (x) dx

(7.6)

1

l

1

l

x +ρ

x

− +ρ

x +ρ

+∞

n

l

(V .P.)

∫

f (x) dx = 2πi

+ πi

(7.7)

Res f (z)

Res f (z) .

∑ z=μk

∑ z=xk

−∞

k =1

k =1

lim max

zf (z)

= 0 .

R

→∞ z CR

Пример 7.1. Вычислить интеграл

+∞

x +1

−∞∫

dx .

(x2 +1)(x2 + 4)

Функция f (z) =

z +1

аналитична в полуплоскости

(x2 +1)(x2 + 4)

z1 = i

и z2 = 2i . Заметим также,

что f (z)

является аналитиче-

ским

продолжением подынте-

гральной функции. Через CR

обозначим контур

{

z

= R, Im z ≥ 0, R > 2}

(рис.7.4).

Покажем,

что

Рис. 7.4

lim max

zf (x)

= 0 .

Действи-

R→∞

z CR

тельно,

zf (z)

=

z(z +1)

=

Reiϕ(Reiϕ +1)

≤

(z2 +1)(z2 + 4)

z=Re

iϕ

(R2 e2iϕ +1)(R2e2iϕ + 4)

R2 (1 +1/ R)

1+1/ R

eiϕ

≤

=

;

=1 .

R4 (1

+1/ R2 )(1+ 4 / R2 )

R2 (1+1/ R2 )(1+ 4 / R2 )

Таким образом,

0 ≤ max

zf (z)

≤

1+1 / R

.

R2 (1 +1 / R2 )(1+

4 / R2 )

z CR

Переходя к пределу в последнем неравенстве, получаем

lim max

z(z +1)

≤ lim

1 +1 / R

= 0 .

(z2 +1)(z2 +4)

1

4

R→∞ z CR

R→∞

R

2

1

+

1+

R

2

R

2

Отсюда следует, что

lim max

zf (z)

= 0 .

R→∞ z CR

Используя утверждение 7.2, получаем

∞

2πi Res f (z) + Res f (z)

∫

f (x) dx =

,

z =2i

z=i

−∞

z +1

i +1

Res f (z) =

(z +i)(z2

+4)

=

(z −i)

′

6

z=i

z=i

+∞

i +1

1 +2i

π

∫

f (x) dx = 2πi

−

=

.

−∞

6i

12i

6

Рассмотрим пример вычисления интегралов вида

+∞∫eikx f (x) dx ,

λ .

−∞

+∞ cos3x dx

Пример 7.2. Вычислить интеграл

∫

. Поскольку

(x

2

+9)

2

0

cos3x

= Re

e3iz

,

(x2 +9)2

(z2 +9)2

z {z: Im z=0}

введем вспомогательную функцию

f (z) =

e3iz

,

которая имеет

(z2 +9)2

три особые точки

z1 =3i , z2 = −3i

– полюса второго порядка и

z3 =∞ – существенно особая точка. При

R > 3 выбираем контур

γR =CR [−R; R] с направлением обхода против часовой стрелки

(рис. 7.5).

Имеет место равенство

e3iz dz

=

e3iz dz

+

R

e3ix

dx = J1 (R) + J2 (R) .

∫ (z2 +9)2

∫ (z2 +

9)2

∫ (x2 +9)2

γR

CR

−R