
Лекция_1
.pdf
Лекция 1. Базовые представления о векторах
1. Вектор можно представить как отрезок, для которого указано где его начало, а где конец. Наглядно – это стрелка. Однако на практике такое определение чаще всего неудобно. Поэтому следует несколько конкретизировать понятие вектора. Для этого представим себе пространство как совокупность точек. Для определения положения точки в этом пространстве необходимо ввести систему координат. Сначала для простоты рассмотрим двумерное пространство. Положение произвольной точки в
декартовой системе координат определяется двумя координатами – проекциями точки на ортогональные числовые оси Ox (ось абсцисс) и Oy
(ось ординат) этой системы с началом отсчета в точке O (рис.1). Например,
координаты точки P равны x |
P1 |
, y |
P1 |
. Каждой паре точек можно сопоставить |
|||||
1 |
|
|
|
|
|
|
|
||
вектор-стрелку. На рис.1 представлены два вектора |
PP |
и Q Q |
. Координаты |
||||||
|
|
|
|
|
1 |
2 |
1 |
2 |
|
вектора определяются разностью соответственных координат точек его
концов. Например, координаты вектора Q1Q2 |
равны: |
|
Q1Q2 xQ 2 xQ1, yQ 2 |
yQ1 . |
(1) |
Таким образом, вектор представляет собой набор чисел, являющихся его координатами в заданной системе координат. Если перейти в другую систему координат, в которой положение eё начала – 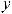
 точки O – несколько смещено, то
точки O – несколько смещено, то  координаты вектора изменятся. Таким
координаты вектора изменятся. Таким
образом, обозначение вектора в духе (1)
предполагает то, что мы знаем о какой
системе координат идет речь. Ориентация
осей системы координат определяется так
называемыми базисными векторами-ортами
Рис.1
– масштабными векторами, длины которых принимаются за единицу. На рис. 1 это векторы i и j. Тройка O,i, j определяет заданную систему координат.
Произвольный вектор (1) можно представить в виде разложения по базисным векторам:
(2)
2. Векторы, сопоставляемые физическим величинам, могут быть
закрепленными (связанными), скользящими или свободными. Свободным вектором называют вектор с фиксированным направлением и величиной, но который можно перемещать параллельно самому себе. Такие векторы описывают векторные физические величины, не меняющиеся при переходе из одной точки пространства в другую. Свободными являются, например,
базисные векторы, векторы угловых перемещений, скоростей, ускорений,
моментов силы, импульса. Свободные векторы можно складывать и умножать, даже если они не имеют общего начала. Для этого просто надо, не меняя длин и направлений, совместить начала векторов. Закрепленным вектором называется вектор, начало которого находится в фиксированной точке. Примером связанного вектора является сила, приложенная к
материальной точке, линейные перемещение, |
||
скорость, ускорение материальной точки. Для |
||
скользящего вектора нельзя указать точку |
||
приложения, а можно говорить только о линии |
||
действия. Примером такого вектора является |
||
сила, приложенная к твердому телу. При |
||
осуществлении |
алгебраических |
операций |
необходимо |
помнить, что связанные и |
|
скользящие векторы можно перемещать только |
Рис.2 |
|
вдоль линий действия. Связанные и скользящие векторы могут быть по правилам линейной алгебры выражены через свободные. Именно поэтому

правила работы с векторными величинами формулируются для свободных векторов.
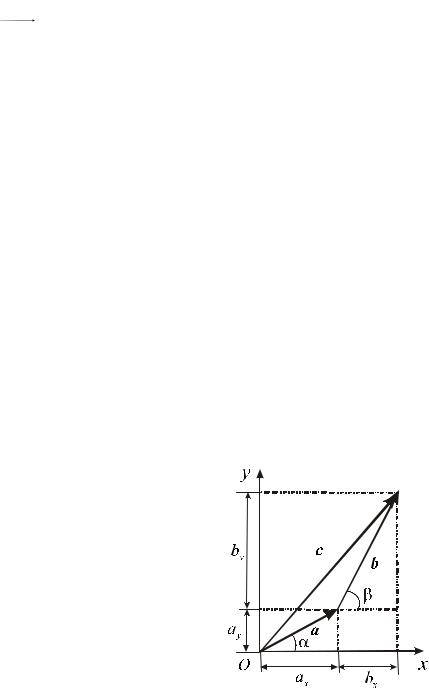
3. Рис.2 иллюстрирует правило определения суммы двух векторов a и b . Для этого начало вектора b совмещают с концом вектора a . Достраивая до треугольника, получают вектор c a b. При этом, как видно из рис.2,
координаты получившегося вектора равны сумме соответствующих координат векторов a и b :
c cxi cy j ax bx i ay by j. |
(3) |
Таким образом, при сложении векторов необходимо просто сложить их соответствующие координаты. Вычитание векторов определяется аналогично: разность векторов a и b эквивалентна сумме векторов a и b :
c a b ax bx i ay by j. |
(3.1) |
Как видно из рис. 2, величина (модуль) вектора определяется согласно теореме Пифагора:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Q1Q2 |
|
|
|
xQ 2 xQ1 |
2 yQ 2 |
yQ1 |
2 , |
|||||||
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(4) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
a |
|
a |
|
|
a2 |
a2 . |
|
|
|
||
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
x |
y |
|
|
|
|
Величина вектора является, разумеется, также и расстоянием между двумя точками: его началом и его концом.
Из рис.2 также следует, что проекции вектора на оси координат определяются через его модуль и углы наклона к соответствующим осям следующим образом:
ax a cos , ay a sin . (5)
4. В трехмерном пространстве положение произвольной точки в декартовой системе координат определяется тремя координатами – проекциями точки P на ортогональные оси Ox (ось абсцисс), Oy (ось ординат) и Oz (ось аппликат) этой системы с началом отсчета в точке O
(рис.3). Вектор r OP , проведенный из начала координат O в точку
P xP , yP , zP , называется радиус-вектором точки P . Коль скоро координаты
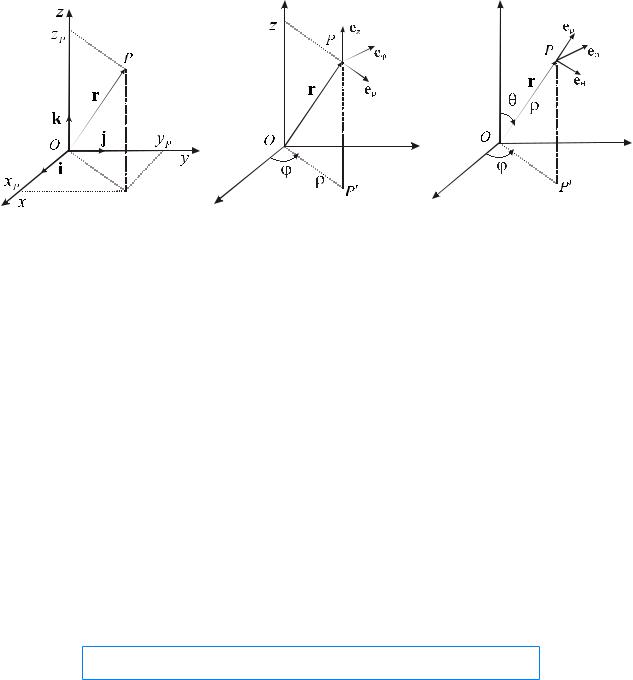
точки O равны нулю, то координатами радиус-вектора являются координаты
его конца, т.е. точки P . В дальнейшем для краткости записи базисные
векторы будем обозначать как ex ,ey ,ez . Радиус-вектор может быть разложен по этим трем векторам:
r xPex yPey zPez . |
(6) |
Рис.3 |
|
Рис.4 |
Рис.5 |
|
Рассмотрим теперь два произвольных вектора |
a axex ayey azez и |
|||
b bxex byey bzez . |
Скалярным произведением этих |
векторов называется |
||
следующая конструкция: |
|
|||
|
|
|
|
|
|
|
ab axbx ayby azbz . |
|
(7) |
|
|
|
|
|
При этом говорят, что определена метрика пространства. В данном случае метрика называется евклидовой. Метрика пространства задаёт правило
определения расстояния между двумя точками. В самом деле, если вектор a |
|
умножить скалярно сам на себя, то получим формулу (4). |
|
5. Помимо скалярного произведения векторов, существует их |
|
векторное произведение, определяемое согласно следующему правилу: |
|
a b c aybz azby ex azbx axbz ey axby aybx ez . |
(8) |
Следует обратить внимание на то, что скалярное произведение – это число
(скаляр), а векторное произведение суть вектор с координатами,

определяемыми согласно (8). Направление и величину этого вектора наглядно можно представить следующим образом.
Направление вектора с перпендикулярно как вектору a , так и вектору b , то
есть вектор c перпендикулярен плоскости, в которой лежат два вектора a и
b , произведение которых мы и находим. Если, например, a и b лежат в плоскости Oxy , то вектор a b c параллелен оси Oz . Чтобы определить,
направлен ли он по оси Oz или против неё, надо воспользоваться правилом правого винта, которое для наглядности сформулируем
так. Шариковую или любую другую ручку с правым |
|
|||||||||
винтом располагаем вдоль вектора c , а затем вращаем |
|
|||||||||
колпачок от первого вектора в произведении (в нашем |
|
|||||||||
случае вектора a ) ко второму (вектору b ). Направление |
|
|||||||||
движения колпачка покажет направление вектора c (рис. |
Рис.6 |
|||||||||
6). Величина вектора c может вычислена согласно |
||||||||||
|
||||||||||
следующей формуле |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
c |
|
a |
|
b |
sin |
, |
(9) |
|
|
|
|
|
|
|
|
|
|
|
|
вкоторой – угол между векторами a и b .
6.Положение точки можно задать также с помощью цилиндрической и сферической систем координат. Цилиндрическими координатами точки P
называют расстояние (полярный радиус) от начала координат до её проекции P на плоскость Oxy (рис. 4), угол (полярный угол) между осью
Ox и направлением , и координату z . Базисные векторы такой системы координат постоянны по модулю, но, в отличие от орт декартовой системы,
при движении точки P меняют свою ориентацию. Про такой базис говорят,
что он локальный (локальный репер), т.е. определен в каждой точке свой.
Радиус-вектор в такой системе координат представим в виде: |
|
r e zez . |
(10) |
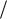
Вектор e |
|
|
направлен вдоль направления OP в сторону его увеличения, а |
||
вектор e |
– по касательной к окружности радиуса |
в сторону увеличения |
угла |
(против часовой стрелки). Связь |
между декартовыми и |
цилиндрическими координатами легко получить, пользуясь рис. 4:
|
|
x cos , y sin , z z. |
|
(11) |
Причем полярный |
угол |
изменяется в полуинтервале |
0,2 , |
полярный |
|
|
|
|
|
радиус в полуинтервале |
0, , а координата z в интервале , . Если |
|||
|
|
|
|
|
зафиксировать значение аппликаты, положив, например, |
z 0 , то формулы |
|||
(11) представляют |
так называемые полярные координаты на |
плоскости |
||
z 0 .
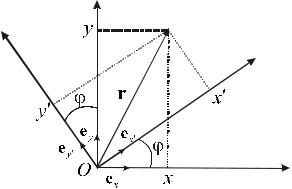
Сферические координаты , , определяются следующим образом
(рис.5): расстояние от начала координат до точки P , угол между осью
Ox и направлением из начала координат до проекции P , и угол |
между |
осью z и направлением . Радиус-вектор имеем вид: |
|
r e . |
(12) |
Из рис. 5 следует, что |
|
x sin cos , y sin sin , z cos . |
(13) |
Проекцией вектора на некоторую ось, направление которой задается единичным вектором e , называется скалярное произведение этого вектора на вектор e . Например, проекция радиус-вектора на ось аппликат равна
rez xex |
yey zez ez |
xexez yeyez zezez z . |
(14) |
||||||
Здесь учтено, что exez |
|
|
ex |
|
ez |
|
cosexez |
1 1 cos 2 0, eyez 0 |
и ezez 1. |
|
|
|
|||||||
Легко видеть, что скалярное произведение определяет угол между произвольными векторами a и b . В самом деле, через два вектора всегда
можно провести плоскость. Выберем в этой плоскости полярные координатыa, 1 для первого вектора и b, 2 для второго, записав указанные векторы в виде (см. рис.2)
a axex |
ayey |
a cos 1ex |
|
|
a sin 1ey , |
|
|||||||
b bxex |
byey |
b cos 2ex |
|
|
bsin 2ey . |
|
|||||||
Тогда согласно (7) их скалярное произведение принимает вид: |
|
||||||||||||
ab ab cos 1 cos 2 absin 1 sin 2 ab cos 1 2 ab cos ab . |
|
||||||||||||
Следовательно, угол между двумя векторами определяется условием: |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
cos ab |
|
|
ab |
|
|
. |
|
(15) |
|||
|
|
|
a |
|
b |
|
|
||||||
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|||||||||||
7. Как отмечалось выше, для задания вектора в трёхмерном |
|||||||||||||
пространстве необходимо задать три его координаты: |
|
||||||||||||
|
|
|
|
|
|
|
|
|
3 |
|
|
||
r xex yey zez x e . |
(16) |
||||||||||||
|
|
|
|
|
|
|
|
1 |
|
||||
Здесь мы для краткости ввели обозначения |
|
|
|
|
|
||||||||
x x1, y x2 , z x3 , ex e1, ey e2 , ez e3.
Если мы теперь переместим начало системы координат из точки O в точку
O на вектор |
|
R X ,Y , Z |
(17) |
и повернем саму систему координат на некоторый угол, то координаты вектора изменятся. При этом, конечно, изменятся и базисные векторы.
Радиус-вектор в новой системе координат связан с радиус-вектором в старой системе координат следующей формулой
|
3 |
3 |
r r R |
или x e x e |
|
|
1 |
1 |
3 |
|
X e . |
(18) |
1
Умножим последовательно равенство (18) скалярно на орты исходной системы координат e :
3 |
3 |
x e e x e e |
|
1 |
1 |
3 |
|
X e e . |
(19) |
1
Учитывая, что скалярное произведение базисных векторов представляют
символ Кронекера:
|
1, |
при |
|
e e |
при , |
(20) |
|
|
0, |
|
|
выражение (19) примет вид |
|
|
|
3 |
3 |
3 |
|
x x cose e X , |
(21) |
||
1 |
1 |
1 |
|
в котором коэффициенты |
|
|
|
|
cose e |
A , |
(22) |
характеризующие ориентацию новой системы координат относительно старой, называются направляющими косинусами. Учитывая определение
(20) и обозначение (22), соотношение радиус-векторов (21) можно представить в виде
3 |
|
x X x A . |
(23) |
1 |
|
Полученное соотношение между старыми и новыми координатами можно записать в развернутом виде:
x X Axx x Axy y Axz z , |
|
y Y Ayx x Ayy y Ayz z , |
(24) |
z Z Azx x Azy y Azz z . |
|
Направляющие косинусы образуют так называемую матрицу поворота осей координат:
ˆ |
|
A |
A |
A |
|
|
xx |
xy |
xz |
|
|
A Ayx |
Ayy |
Ayz . |
(25) |
||
|
|
A |
A |
A |
|
|
|
zx |
zy |
zz |
|
В случае, когда R 0 , мы имеем дело только лишь с преобразованием базисных векторов без их параллельного переноса. Тогда (23) принимает вид:
3 |
|
x A x . |
(26) |
1
Раньше уже было отмечено, что вектор представляет собой набор трех чисел.
Но не всякая физическая величина, характеризуемая тремя числами, является
вектором. Чтобы физическая величина была вектором, необходимо, чтобы эти три числа вели себя при переходе из одной системы координат в другую
как компоненты радиус-вектора при преобразованиях (26). Ниже мы уточним данное определение.
Выражение (26) можно представить в векторно-матричном виде:
x |
|
|
|
Axx |
Axy |
y |
|
|
A |
A |
|
|
|
|
|
yx |
yy |
z |
|
|
|
A |
A |
|
|
|
|
zx |
zy |
Axz
Ayz
Azz
x |
|
|
|
|
|
, |
(27) |
y |
|
||
z |
|
|
|
|
|
|
|
определив тем самым, правило перемножения матрицы на вектор. Согласно
(27), например, для вычисления первой компоненты x вектора |
r , |
надо |
сложить произведения элементов первой строки матрицы |
ˆ |
на |
A |
||
соответствующие компоненты вектора r . |
|
|
Рис.7
Заметим, что вектор можно представить либо в виде строки (1), либо в виде столбца, как мы это сделали в соотношении (27). Оба способа представления равноправны. Только надо иметь в виду, что определив,
например, вектор в виде строки, его запись в виде столбца будет означать его транспонирование. Под транспонированием понимают операцию замены строк столбцами и наоборот. Т.е.
x |
|
|
|
|
|
T |
(28) |
y |
x, y, z . |
||
|
|
|
|
z |
|
|
|
Скалярное произведение (7) при этом можно представить в виде матричного умножения вектора a на транспонированный вектор b
|
bx |
|
|
|
|
|
|
ab axbx ayby azbz |
|
|
ax |
,ay ,az bx |
,by |
,bz . |
(29) |
ax ,ay ,az by |
|||||||
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
|
bz |
|
|
|
|
|
|
Рассмотрим поворот осей координат на угол в плоскости z 0 . Из рис. 7
видно, что связь между ортами начальной и повернутой систем координат представима в виде
|
|
ex ex cos ey sin , |
|
|
|
||
|
|
ey |
ex sin ey cos , |
|
|
(30) |
|
|
|
|
ez ez . |
|
|
|
|
Поэтому |
exex Axx |
cos , |
exey Axy sin , |
eyex Ayx sin |
и |
||
eyey Ayy cos . Учитывая, |
что |
координата z |
вектора при |
этом |
не |
||
изменяется, |
получим |
соотношение, |
определяющее |
с помощью |
матрицы |
||
ˆ |
|
|
|
|
|
|
|
поворота Az переход от нового вектора r к старому r : |
|
|
|||||
xyz
cos
sin0
sin |
0 |
x |
|
|
|
cos |
0 |
|
|
ˆ |
(31) |
y |
|
или r Az r |
|||
0 |
1 |
|
|
|
|
z |
|
|
|
|
|
ˆ |
определяет переход от старого вектора |
||||||
Матрица обратного поворота Az |
|||||||||
r к новому r : |
|
|
|
|
|
|
|
|
|
|
|
|
|
ˆ |
r . |
|
|
|
(32) |
|
|
r Az |
|
|
|
||||
Непосредственным вычислением нетрудно показать, что |
|
|
|||||||
|
|
ˆ |
|
ˆ |
ˆ |
ˆ |
|
|
|
|
|
det Az 1, |
Az Az |
E, |
|
(33) |
|||
ˆ 1 |
ˆ |
ˆT |
|
|
ˆ |
ˆ |
ˆ |
|
|
|
|
1 |
2 , |
||||||
Az |
Az Az |
, Az 1 |
Az 2 |
Az |
|||||
где ˆ – единичная матрица (матрица, все элементы которой равны единице),
E
ˆ |
ˆ 1 |
– матрица, обратная |
ˆ |
|
det Az – |
определитель матрицы, Az |
к Az . |
||
Напомним, |
|
ˆ 1 |
ˆ |
ˆ |
что по определению обратного элемента Az |
Az |
E . Под |
||
определителем матрицы понимают следующую конструкцию:
