Добавил:

AD Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Тверской Государственный Университет

Предмет:

Векторный и тензорный анализ

Файл:

Лекция 11

.pdf

Скачиваний:

Добавлен:

21.12.2022

Размер:

682.33 Кб

Скачать

☆

Лекция 11. Дифференциальные операции в криволинейных

координатах

1. Градиент в криволинейных системах координат. Дифференциал скалярного поля f r можно представить в виде

dq1

dq2

dq3

(189)

e1dq1

e2dq2 e3dq3 .

Второй множитель в последней строке – это дифференциал радиус-вектора.

Следовательно, первый множитель – это градиент:

gradf e1	f	e2	f		e3	f		.	(190)
	1		q	2		q	3
	q

Градиент представляет собой геометрический объект, имеющий по определению разложение по взаимному базису ek . Говорят, что градиент – это ковектор. Чтобы его преобразовать в вектор (перейти к контравариантным компонентам), необходимо перейти к разложению по исходному базису ei :

gradf ek	f	e	gik	f	.	(191)
	qk			qk
		i

Следовательно, компоненты вектора-градиента имеют вид:

gradf i gik

(192)

В ортогональной системе координат

Поэтому выражение

для

градиента можно преобразовать:

1 f

gradf ei H 2

(193)

Во введенном ортонормированном базисе компоненты вектора-градиента

имеют вид (физические компоненты вектора):

f i

(194)

2.Производная от вектора в криволинейных системах координат.

Найдем производную от вектора v v e

по координате x :

v e

x e v

x .

(195)

Но согласно (93)

e .

Указание: повторить материал лекций 4 и 5. Следовательно, (195) можно переписать в виде

			v
	v	e		v	e v e .	(196)
x	v	e	x	v	e v e .	(196)
x			x

Здесь мы ввели ковариантную производную от вектора:

v	v	v .	(197)
	x

Как видно, использование ковариантной производной позволяет выносить базисный вектор за скобку. Это очень удобное в использовании свойство.

Задание 42. Показать, что

e . Указание: Используйте e e

e e

и (92).

v .

3.Дивергенция в криволинейных системах координат.

Дивергенцией векторного поля называется свертка

divv	v	v	v	.	(198)
		x

В декартовых координатах символы Кристоффеля равны нулю. Поэтому дивергенция принимает вид (145). В общем случае, как может показаться,

всегда приходится считать символы Кристоффеля. Но, как мы увидим ниже,

формулу (198) можно представить в виде, не содержащим символы Кристоффеля. Для этого докажем следующее соотношение:

		dg gg dg		.		(199)

В самом деле, в силу (60.1) имеем
	g	1	g g		.	(200)
			g g		.	(200)
	g	6
	g	6

Это – алгебраическое дополнение. Следовательно, компоненты тензора,

обратного к метрическому, имеют вид:

			g
g		1	g	.
g				.
	g	g g

Так как дифференциал определителя метрического тензора равен

dg g dg ,

то с учетом (201) получаем соотношение (199).

Задание 43. Показать, что

a.dg g g dg .

b.dg gg dg .

Указание: используйте соотношение g g .

Из (199) следует полезное для дальнейших выкладок равенство:

1	g	g	g	.
g x
			x

Найдем . Согласно (95) и (96) запишем

Раскрывая скобки, получим

(201)

(202)

(203)

В силу (203) выражение (204) принимает вид:

2g x

В результате выражение для дивергенции (198) имеет вид:

divv

1 g

g x

В ортогональных координатах

g H

v .

Значит, дивергенция принимает вид

H2 H3v1ф

H1H3vф2

H1H

2 v3ф

divv

Задание 44. Вывести формулу (208) самостоятельно.

(204)

(205)

(206)

(207)

(208)

4. Лапласиан скалярного поля. В силу определения оператора

Лапласа (173) имеем:

f f	1			f .
			g

		g x

Согласно (192) перепишем (209) в окончательном виде:

g g

g x

В ортогональных координатах Лапласиан скалярного поля имеет вид:

f	1				H2 H3 f						H1H3 f						H1H2 f
																					.
	H H	H		1	H		1		x	2	H		x	2	x	3	H		x	3	.
	H H	H		x	H	1		x	x		H	2	x		x		H	3	x
	1 2		3			1						2						3

(209)

(210)

(211)

Задание 45. Вывести формулу (211) самостоятельно.

5.Ротор в криволинейных системах координат. Согласно (126) и

(169) выражение для ротора следует записать в виде:

rota a
		a e .	(212)

	g x

Из выше изложенного видно, что при переходе к криволинейным координатам обычная частная производная заменяется на ковариантную.

Таким образом, например, мы получили выражение для дивергенции (198).

Может и в (212) тоже следует произвести такую замену? Оказывается, что в этом нет необходимости. Дело в том, что в (212) производные стоят не поодиночке, а представлены в виде разностей

a a .x x

Но, как легко убедиться, эти разности не изменятся, если в них частные производные заменить на ковариантные:

(213)

Здесь мы учли, что символы Кристоффеля симметричны по двум нижним индексам.

Таким образом, ротор вектора является геометрическим объектом,

контравариантные компоненты которого находятся по формуле

rota		a
			.	(214)
		x
	g

Ковариантные компоненты находим по общим правилам:

rota		rota
rota	g	rota	g		a .	(215)
				g
				g

Так как g и a g a , то (215) принимает вид

rota
	g	g	g		a .	(216)
	g	g	g		a .	(216)
				g
				g

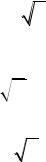
С использованием (60.1) можно показать, что
g	g	g	g.	(217)

Задание 46. Вывести соотношение (217).

Следовательно, (215) примет вид:

rota
	g a .		(218)

Можно ввести геометрические объекты

e 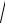g ,

e		(219)

		,
	g	,
	g

которые, при замене координат преобразуются как компоненты абсолютно антисимметричного тензора (существующие нюансы будут рассмотрены в в лекциях по тензорному анализу).

Задание 47. Используя (212), (126) и (127), показать, что в ортогональных координатах ротор принимает вид:

e1*

e*2

e*3

rota

(220)

H1 x1

H2 x2

H3 x3

a1ф

a2ф

a3ф

Задание 48.

1.Вычислить физические компоненты градиента скалярного поля,

записанного в цилиндрических координатах:

a.f cos ,

b.f e z n cos n ,

c.f 2 2 cos ez sin ,

d.f cos z sin2 3 .

2.Вычислить физические компоненты градиента скалярного поля,

записанного в сферических координатах:

a.f r2 cos ,

b.f 1r cos kr cos ,

c.f r12 3cos2 1 sin 2 ,

d.f 3r2 sin e r cos r .

3.Найти уравнение векторных (силовых) линий следующих полей,

записанных в цилиндрических или сферических координатах:

a.a e e ez ,

b.a e e zez ,

c. a	2c cos	e		csin	e .

	r3		r	r3

4.Вычислить дивергенцию векторного поля, компоненты которого заданы в цилиндрических координатах:

a.a

b.a

0 ,

a c 2		2		0;
	R2		, az
		2

a 0 , az c R2 2 ;

c.a ф 2 R cos , a ф R r sin , azф 0 ;

d.aф , aф z sin , aфz e coscz .

5.Вычислить дивергенцию векторного поля, компоненты которого заданы в сферических координатах:

cos

, a cr

sin , a 0

;

ar c

cos , a c

sin ,

0 ;

arф 2r c cos , a ф

csin , a ф r sin ;

d. ar	2cos	, a	sin	, a	0 .
	r3		r3
ф		ф		ф

6. Найти лапласиан скалярного поля, заданного в цилиндрических координатах:

a. f cR3 cos ;

b. f c 3R 2 cos ; c. f 2 z2 cos .

7. Найти лапласиан скалярного поля, заданного в сферических координатах:

a. f rc3 3cos2 1 ; b. f cr sin2 cos 2 .

8. Выяснить, являются следующие поля потенциальными. Если это так, то найти их потенциалы.

a. a e e zez ;

a e sin e

cos e

2ze

;

a er

e ;

;

sin

2cos

sin

e .

9.Вычислить физические компоненты лапласиана векторного поля,

компоненты которого заданы в цилиндрических координатах:

a.a ф 0 , a ф c , azф 0 ;


b.	a ф	0 , a ф	c R		, azф	0 .

				2

Указание: Используйте тождество (185) a = grad diva rot rota .

10.Вычислить физические компоненты лапласиана векторного поля,

компоненты которого заданы в сферических координатах:

, a

sin ;

rф

arф

, a ф

cr sin

Указание: Используйте тождество (185) a = grad

diva rot rota .

Соседние файлы в предмете Векторный и тензорный анализ

#
21.12.2022653.24 Кб2v9DcYFk7dtU.jpg
#
21.12.2022658.7 Кб2Yzdxu2S6R5E.jpg
#
21.12.2022385.42 Кб0_xiLm2mAXB4.jpg
#
21.12.2022615.04 Кб7ВиТА _Физика тест(который будет в конце семестра ) .pdf
#
21.12.2022682.33 Кб8Лекция 11.pdf
#
07.11.2022682.31 Кб5Лекция 6.pdf
#
07.11.2022713.53 Кб4Лекция 7.pdf
#
07.11.20221.23 Mб10Лекция_1.pdf
#
07.11.2022708.28 Кб7Лекция_2.pdf
#
07.11.2022853.22 Кб10Лекция_3.pdf