
Операции с тензорами 15.12
.pdf
|
|
|
|
|
|
|
Операции с тензорами |
|
|
|
|
|
||||||
1. |
Сложение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X 1 2 ... p x Y 1 2 ... p x Z 1 2 ... p x |
|
|
|
|||||||||
|
|
|
|
|
|
|
1 2 ... q |
|
|
1 2 ... q |
1 2 ... q |
|
|
|
|
|||
2. |
Свертка |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X 1 2 ... ... p x X 1 2 ... ... p |
x Tr X X |
1 2 ... 1 1... p x |
|||||||||||||||
|
|
... ... |
q |
|
|
... ... |
q |
|
|
... |
|
... |
q |
|||||
|
1 2 |
|
|
|
|
1 2 |
|
|
|
|
|
1 2 |
1 |
1 |
|
|||
3. |
Тензорное произведение |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
X x Y x Z x |
|
|
|
|
|
|
|
|
|
|||||||
|
|
1 2 ... p |
1 2 ... n |
|
|
|
|
1 2 ... p 1 2 ... n |
|
|||||||||
|
|
X 1 2 ... q |
x Y 1 2 ... m |
x X x Y x |
1 2 |
... q 1 2 ... m |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Пример. Диада. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
компоненты |
|
|
|
||
|
X x X |
|
|
|
|
|
|
|
|
|
|
тензора |
|
|
|
|
||
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
X Y X e Y e |
X Y |
e e |
|
|||||||||||||
|
Y x Y e |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
базис |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Произвольный тензор можно записать в виде:
X X 1 2 ... p e |
e |
... e |
e 1 e 2 ... e q |
1 2 ... q 1 |
2 |
p |
|
|
|
|
базис |
Пример. Произведение двух тензоров, взятых в разных точках пространства, не является тензором.
|
|
Z |
|
X |
|
x Y |
|
|
преобразование |
координат |
Z |
|
X |
|
x |
Y |
|
|
x |
|
|||||||||||||||||||||||
X x |
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Y x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Так как X x и Y x – тензоры, то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
X |
x |
X |
|
x |
x |
|
x |
x |
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
Y |
|
x |
|
|
Y |
|
x |
|
x |
|
x |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
Z |
X |
|
x |
|
x |
|
Y |
|
x |
|
x |
|
x |
|
x |
|
|
x |
|
x |
|
|
|
|
||||||||||||||
|
|
|
|
|
x |
|
x |
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Если бы Z |
был бы тензором, то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
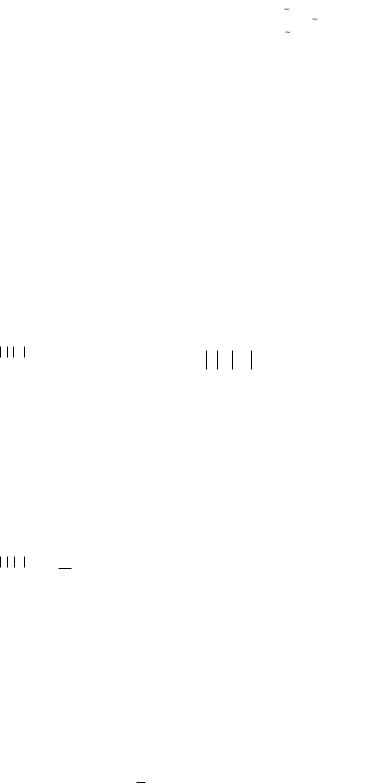
Z Z |
|
x |
|
x |
|
x |
|
x |
|
x |
|
x |
|
X |
|
x |
|
x |
|
Y |
|
x |
|
x |
|
x |
|
x |
|
x |
|
|
x |
|
|
|
|
x |
|
x |
|
|
|
|
|
|
|
x |
|
x |
|
|
Но производные, взятые в разных точках, вообще говоря, не совпадают:
|
|
x |
|
|
x |
|
|
|
||
|
|
x |
x |
|
||||||
|
|
x |
x |
|||||||
4. Симметрирование |
|
|
|
|
|
|
|
|
|
|
1 2 ... p |
|
|
|
|
|
|
|
|
|
|
X X 1 2 ... q |
|
|
|
|
|
|
|
|
||
SymX 1 2 |
... p X 1 2 ... p |
|
|
1 |
|
|
||||
|
|
|||||||||
1 2 |
... q |
|
1 2 ... q |
|
q! 1 2 ... |
|||||
|
|
|
|
|
|
|
||||
аналогично и для верхних индексов.
Пример. |
X X |
1 |
|
X |
1 |
X X |
|
2! |
2 |
||||||
|
|
|
|
||||
Пример. Хотим симметрировать X ijklmnp по индексам i,
X i j k lm n p – симметрирование: i j k lm n p
ikn чёт
|
X 1 2 ... p |
q |
1 2 ... q |
|
k, n . Пишем так:
kin |
нечёт |
ikn ink |
нечёт |
nki |
нечёт |
nik |
чёт |
kni |
чёт |
X i j k lm n p 3!1 X ijklmnp X kjilmnp X ijnlmkp X njklmip X njilmkp X kjnlmip
5. Альтернирование
X X 1 2 ... p1 2 ... q
1 2 |
... p |
|
1 2 ... p |
|
|
1 |
|
|
sign |
1 2 ... p |
||||
AltX |
1 2 |
... q |
X |
1 2 |
... q |
|
|
|
1 |
|
X |
... |
q |
|
|
|
|||||||||||||
|
|
|
q! 1 2 ... q |
|
|
1 2 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Пример. X X 12 X X .

Замечание: |
X X |
X |
1 |
X X |
1 |
X X |
|
|
|
||||||||||||||||||
2 |
2 |
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
1 |
|
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
i |
j |
k |
lm |
n |
p |
ijklmnp |
|
|
|
kjilmnp |
|
ijnlmkp |
|
|
njklmip |
|
njilmkp |
|
kjnlmip |
|||||||
|
|
|
|
|
|
|
|
|
|
X |
X |
X |
X |
X |
|||||||||||||
Пример. |
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
3! |
|
|
|
|
|
|
|
|||||||||||||||
Кососимметрический (антисимметрический) тензор – тензор, инвариантный относительно операции альтернирования по некоторой группе индексов. Если инвариантность по всем индексам, то тензор называется полностью антисимметрическим.
Оператор проектирования – аффинор вида:
|
|
|
|
|
|
T n n |
где n nie , |
|
n |
|
1. Подействуем этим тензором на некоторый вектор v и |
||
|
|
|||||
i |
|
|
|
|
|
|
получим новый вектор u : |
|
|||||
u Tv |
ui |
Tjiv j g jkT ik v j g jk ni nk v j g jk v j nk ni ni nv |
||||
|
|
|
|
|
|
nv |
Вектор u направлен вдоль вектора n , а длина его равна скалярному произведению
nv .
При определенном выборе вектора v может оказаться, что после действия на него аффинором, задаваемым симметричным тензором, изменилась только длина вектора v , но не его направление:
u Tv v
Тогда – собственное значение, v – собственный вектор.
Tkj vk v j gijTkj vk gijv j Tik vk gik vk
СЛАУ
Tik gik vk 0
Собственные значения определяются из уравнения

det Tik gik 0
Вообще говоря, тензор может иметь комплексные значения. Тогда полагают тензор не симметричным, а самосопряженным. По определению оператор T называется
эрмитово сопряженным, если T |
T * . Самосопряженным называется оператор, |
||
ik |
ki |
|
|
который совпадает с эрмито сопряженным: T T , T |
T* . |
|
|
|
ik |
ki |
|
Скалярное произведение в комплексно-значных векторов uv u*i v |
vu * . |
||
|
|
i |
|
Собственные значения самосопряженного оператора действительные. В самом, деле,
|
|
|
|
|
Tik vk vi |
Tik vk * vi * Tkiv*k |
*vi* |
|
||||||||||||||
|
|
k |
v |
*i |
viv |
*i |
|
|
k |
v |
*i |
viv |
*i |
|
|
|
|
|
|
|||
|
|
Tik v |
|
|
|
|
Tik v |
|
|
0 |
* |
viv |
*i |
|
||||||||
|
|
T v*k vi *v*vi |
|
T v*ivk |
*v*vi |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
ki |
|
|
|
i |
|
|
|
ik |
|
|
i |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Пусть 1 |
и 2 |
– различные собственные значения тензора T . |
|
|
||||||||||||||||||
T vk v |
|
|
T vk u*i |
v u*i |
Tik vk u*i 1viu*i |
|
|
|
|
|||||||||||||
|
ik |
|
|
|
|
|
ik |
|
|
1 i |
|
|
|
|
|
* |
|
|
|
|||
|
|
|
1 i |
|
|
|
|
|
|
T uk v*i viu* |
|
|
|
|||||||||
T uk u |
|
T uk v*i |
u v*i |
|
|
|
||||||||||||||||
|
ik |
|
|
2 i |
|
|
ik |
|
|
2 i |
|
|
|
ik |
2 i |
|
|
|||||
|
T vk u*i v u*i |
|
T vk u*i |
v u*i |
0 |
v u*i |
v u*i 0 |
|||||||||||||||
ik |
|
|
|
1 i |
|
|
|
ik |
|
|
1 i |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
T vk u*i |
|
|
|
|
1 |
2 |
i |
|
i |
||
|
|
T viu*k viu* |
|
v u*i |
|
|
|
|
|
|||||||||||||
|
|
ki |
|
|
|
2 i |
|
|
ik |
|
|
2 i |
|
|
|
|
|
|
|
|
||
Т.е. собственные векторы, соответствующие различным собственным значениям, ортогональны.
Ортогональность собственных векторов дает возможность выбрать систему координат, в которой оси направлены вдоль собственных векторов. Такая система координат называется главной системой координат тензора. Компоненты тензора в этой системе координат образуют диагональную матрицу. В самом деле, пусть собственные векторы нормированы: vki ik . Здесь i – номер вектора. Тогда
T j vk |
v j |
T j k k |
|
T j k |
||
k i |
i i |
k i |
i i |
|
i |
i i |
В вещественном пространстве самосопряженному тензору отвечает симметричный тензор. Тогда приходим к известному из алгебры утверждению, что всякую симметричную матрицу можно привести к диагональному виду.
Рассмотрим подробнее
det Tik gik 0
|
|
|
|
T11 |
T12 |
|
T13 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
T21 |
T22 |
T23 |
|
|
0 |
|
|
|
|
|
|
|
||||||
|
|
|
|
T31 |
T32 |
|
T33 |
|
|
|
|
|
|
|
|
|
|
|
||||
3 2 T T T |
|
|
|
T |
T |
|
T |
T |
|
|
|
T |
T |
|
|
|
T11 |
T12 |
T13 |
|
||
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||
|
|
22 |
32 |
|
11 |
21 |
|
|
11 |
31 |
|
|
|
T T |
T |
0 |
||||||
11 |
22 |
33 |
|
|
|
T23 |
T33 |
|
T12 |
T22 |
|
|
|
T13 |
T33 |
|
|
|
21 |
22 |
23 |
|
|
|
|
|
|
|
|
|
|
|
|
T31 |
T32 |
T33 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Так как – скаляры, то коэффициенты этого уравнения также инвариантны относительно преобразований координат. Три инварианта тензора второго ранга.
|
I T |
T |
T |
SpT g |
T ij T i |
|
|
|
|
|
|||||||||||
|
|
1 |
|
|
11 |
22 |
33 |
|
|
|
|
ij |
|
i |
1 |
|
2 |
3 |
|
|
|
|
|
|
T32 |
|
|
T21 |
|
T11 |
T31 |
|
|||||||||||
I |
2 |
|
T22 |
|
T11 |
|
|
||||||||||||||
|
|
|
T23 |
T33 |
|
T12 |
T22 |
|
T13 |
T33 |
1 |
2 |
1 |
3 |
2 |
3 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
T11 |
T12 |
T13 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
I |
3 |
|
T |
T |
T |
|
det T ijkT T T |
|
|
|
|||||||||
|
|
|
|
21 |
22 |
23 |
|
|
|
|
1i 2 j 3k |
|
1 2 3 |
|
|
||||||
|
|
|
|
|
|
T31 |
T32 |
T33 |
|
|
|
|
|
|
|
|
|
|
|
||
Тензор, у которого инвариант I1 0 , называется девиатором.
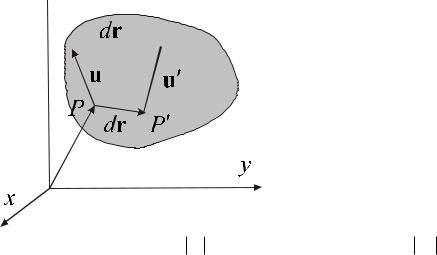
Пример. Тензор деформаций. В общем случае деформация является неоднородной. Тело испытывает разную деформацию в различных направлениях. Для описания такой деформации необходимо ввести тензор деформаций. Для того чтобы понять как появляется тензор деформаций, рассмотрим как изменяется положение каждой частицы 
 физически бесконечно малого объёма. Смещение
физически бесконечно малого объёма. Смещение  каждой точки P можно охарактеризовать
каждой точки P можно охарактеризовать  вектором смещения u r , являющимся при
вектором смещения u r , являющимся при
|
|
|
неоднородных деформациях функцией координат. |
||||
|
|
|
Деформации в точке будут определены лишь |
||||
|
|
|
тогда, когда известно смещение соседних с точкой |
||||
|
|
|
Р частиц тела. Таким образом, задание смещения |
||||
|
|
|
всех частиц тела полностью определяет его |
||||
|
|
|
деформацию. |
В самом деле, |
рассмотрим |
две |
|
|
|
|
бесконечно близкие точки |
P и |
|
При |
|
|
|
|
P . |
||||
|
|
|
недеформированном состоянии расстояние между |
||||
этими точками равно dl dr , а после деформации – |
dl dr . Если при этом смещение |
||||||
точки P равно u , а точки |
|
|
u r dr , то, как видно из рис., |
|
|
|
|
P |
– u |
|
|
|
|||
dr dr + u r dr u r dr du
В декартовых координатах
dx dx u dx x
Здесь
A u
x
тензор относительной деформации. Разложим его на симметричную и кососимметричную части:
A |
1 |
|
u |
|
u |
|
1 |
|
u |
|
u |
|||
|
|
|
x |
|
|
|
|
x |
|
|||||
2 |
2 |
|||||||||||||
|
|
x |
|
|
|
|
x |
|
|
|||||
Опр. Тензор деформации – симметричная часть тензора относительной деформации
|
|
1 |
|
u |
|
u |
||||
|
|
x |
|
x |
|
|
||||
2 |
||||||||||
|
|
|
|
|
|
|
||||
Опр. Тензор поворота – кососимметричная часть тензора относительной деформации
|
|
1 |
u |
|
u |
||
|
|
|
|
|
|||
|
|
||||||
|
|
2 |
|
x |
|||
|
|
|
x |
|
|
||
Симметричный тензор можно представить в виде суммы шарового тензора и девиатора:
|
|
|
|
|
|
|
1 |
|
|
u |
|
|
u |
|
|
|
|
|
|
|
Sp Dev |
|
||
|
|
Sp |
|
|
|
|
|
|
|
|
|
|
Sp |
|
||||||||||
|
|
|
|
x |
|
x |
|
|
|
|
||||||||||||||
|
3 |
|
|
|
|
2 |
|
|
|
|
|
|
3 |
|
|
3 |
|
|
|
|||||
В главных осях |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
du dx |
|
|
|
|
|
|
|
|
dx |
dx 1 |
|
|
||||||||||||
|
dx dx |
|
||||||||||||||||||||||
V V |
|
|
|
|
|
|
|
|
dx1dx2dx3 1 11 1 22 1 33 |
|
||||||||||||||
|
dx1dx2dx3 |
|
||||||||||||||||||||||
V 1 11 |
22 |
33 V 1 Sp |
|
|
|
|
|
|
||||||||||||||||
V V |
Sp |
|
u |
divu |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
V |
x |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таким образом, относительное изменение объема при деформации определяется диагональными компонентами тензора деформации.
Недиагональные элементы определяют сдвиговую деформацию, а диагональные – относительное изменение длин отрезков.

Кососимметрическая часть определяет повороты объема как целого вокруг некоторой оси вращения. Действительно, Та часть изменения вектора u , которая связана с тензором
, равна |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
du |
|
|
dx |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
Но кососимметрическому тензору |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
0 |
|
|
|
|||
|
|
|
|
|
|
|
12 |
|
13 |
|
|
|
|
|
0 |
|
|
||||||
|
|
|
|
21 |
|
|
|
23 |
|||
|
|
|
|
|
31 |
32 |
0 |
|
|||
|
|
|
|
|
|
||||||
можно сопоставить дуальный псевдовектор
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
|
|
|
|
|
|
2 |
|
123 |
23 |
|
2 |
|
132 32 |
|
23 |
|||||||
|
|
|
|
1 |
|
|
|
|
2 |
|
1 |
|
2 |
|
1 |
213 13 |
|
1 |
231 31 |
31 |
||||||||||||||||||
|
|
2 |
|
|
2 |
|
2 |
2 |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
2 |
|
|
|
|
|
2 |
312 |
12 |
|
2 |
321 21 |
|
12 |
||||||||||
Задание. Показать, что |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Поэтому |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
3 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
Тогда
du1 12dx2 13dx3 3dx2 2dx3 du2 21dx1 23dx3 3dx1 1dx3
du3 31dx1 32dx2 2dx1 1dx2
Или
du dx dx dx du φ dr
Здесь φ 1, 2 , 3 32 , 13 , 21 .
Задание. Показать, что φ 12 rotu .
В криволинейных координатах

12 u u
Задание. Запишите в явном виде компоненты тензора деформации в декартовой, цилиндрической и сферической системах координат. Запишите также физические компоненты тензора деформации в этих координатах.
Пример. Пространство Минковского E4 с метрикой G diag 1, 1, 1, 1 . Тензор электромагнитного поля
|
|
0 |
|
Ex |
Ey |
Ez |
|
|
|
|
Ex |
|
|
H3 |
|
|
|
F F |
|
0 |
H2 |
|||||
|
E |
|
H |
|
0 |
H |
|
|
|
|
|
||||||
|
|
|
y |
|
3 |
|
1 |
|
|
|
Ez |
H2 |
H1 |
0 |
|
||
Задание. Найти F .
Тензор электромагнитного поля определяется 4-вектором потенциала
A , A
A , A
A g A
посредством следующей формулы
F A A
x x
Уравнение движения точечной заряженной частицы
|
|
|
|
|
|
|
m |
du |
|
e |
F |
u |
|
|
|
|
|
|
|
d |
|
||||
|
|
|
|
|
|
|
|
|
c |
|
||
|
|
v 2 |
ds |
|
|
|
|
|
|
|||
d |
1 |
|
|
dt |
|
– собственное время. |
|
|
|
|
||
|
|
|
|
|
|
|||||||
|
|
c |
|
c |
|
|
|
|
|
|
||
|
|
dx |
|
|
|
d |
|
|
|
dt |
|
dr dt |
|
dt |
dr |
|
||||||
u |
|
|
|
|
|
|
ct, r c |
|
, |
|
|
|
|
|
|
c, |
|
|
|
|||
d |
d |
d |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
dt d |
|
d |
dt |
|
||||||||||
u |
|
|
|
1 |
|
|
|
|
|
c, v |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
v 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
1 |
|
|
|
c, v |
|
|
|
|
|||
|
|
|
|
|
|
|
v 2 |
||||
1 |
|
|
|
|
|
|
|
|
|||
|
c |
|
|
||
Задание: Записать пространственную часть уравнения движения частицы. Убедиться, что
E |
1 |
A |
, |
H rotA |
|
c |
t |
||||
|
|
|
Задание. Показать, что инварианты электромагнитного поля имеют вид
E2 H2 invar,
EH 2 invar

Опр. Относительным тензором p q ранга называется геометрический объект, компоненты которого преобразуются по закону:
|
|
|
|
|
|
|
|
|
|
x 1 |
x 2 |
|
x |
|
|
x 1 |
|
x 2 |
|
x |
|
|
T 1 |
2 |
... |
p |
|
|
w |
|
... |
|
|
p |
|
|
|
|
q |
||||||
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
T 1 |
2 p |
|
|
... |
|
|
|
|
|
|
... |
|
|
|
||||
... |
|
|
... |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
x 1 |
x 2 |
|
x p |
|
x 1 |
|
x 2 |
|
x q |
||||||
1 2 |
|
q |
|
|
|
|
1 2 |
|
q |
|
|
|
|
|||||||||
det xix j
1
|
При 1 |
и w 0 объект T |
– истинный тензор |
|
При 1 |
и w 0 объект T |
– относительный тензор веса w |
При 1 и w 0 объект T – псевдотензор
При 1 и w 0 объект T – относительный псевдотензор веса w
Пример
g |
|
g |
|
xi |
|
xk |
|
xk |
g |
|
xi |
|
G J T GJ |
|
i k |
ik xi xk |
xk |
ik xi |
|||||||||||
|
|
|
|
|
|
|||||||||
Но
det G det J |
T |
|
|
2 |
det G |
|
GJ det J |
||||
g |
|
|
|
|
g |
|
|
|
|
|
|
Тогда
g 2 g
Определитель метрического тензора – это относительный скаляр веса 2.
Пример
|
xi |
|
|
x1 |
|
x2 |
|
x3 |
|
det |
|
i1 i2i3 |
|
|
|
|
|
|
|
x j |
i |
|
i |
|
i |
||||
|
|
|
x 1 |
|
x 2 |
|
x 3 |
|
|
|
|
xi1 |
xi2 |
xi3 |
|
|
|
||
i1i2i3 i1 i2i3 |
xi1 |
xi2 |
xi3 |
|
|
|
|||
|
|
|
|
|
|||||
Аналогично
|
1 |
xi1 |
xi2 |
xi3 |
i1 i2i3 |
|
i1i2i3 |
|
xi3 |
|
|
|||
|
|
xi1 |
xi2 |
Но
