2 .4.8 Шестнадцатерично–двоичные преобразования. Преобразование смешанного шестнадцатеричного числа в двоичную систему счисления.

В смешанном числе преобразования целой и дробной части проводятся раздельно по соответствующим рассмотренным ранее алгоритмам.

Из разложений 1.6 и 1.7 вытекает следующий алгоритм конвертации шестнадцатеричного числа в двоичную систему счисления.

1. Каждая цифра шестнадцатеричного числа заменяется соответствующей двоичной тетрадой

2. Незначащие старшие и младшие нулевые разряды соответственно в целой и дробной части двоичного числа для “ вписывания ” в заданную разрядную сетку могут быть отброшены

3. Положение запятой и знак числа – сохраняются.

П ример 20. Преобразовать шестнадцатеричное число XH= 9F,C47GH в двоичную систему счислении.

Формализованная запись задания 9F,C47H → XB

П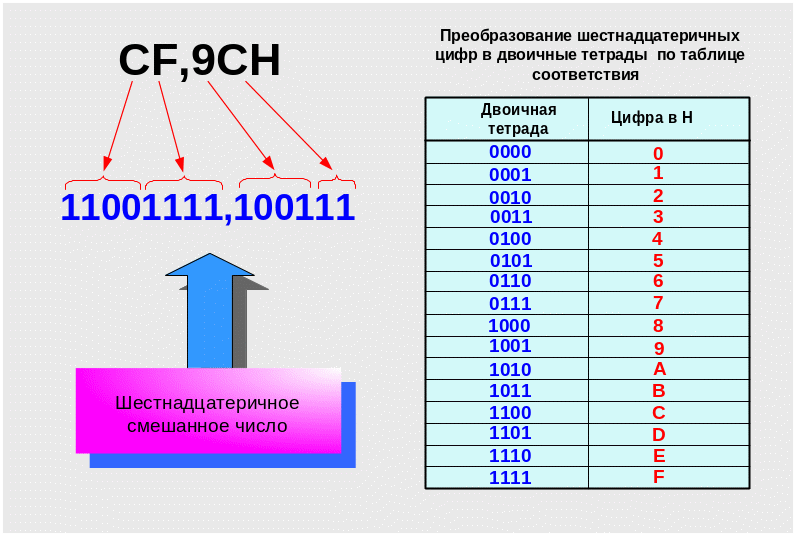 роцедура преобразования в этом случае поясняется рисунком

2.5 Преобразования “через промежуточную систему”

Преобразования через “промежуточную систему” основываются на рассмотренных ранее методах 1–4. Такая процедура преобразования может быть эффективна в трех случаях:

1. если требуется преобразовать исходное число в несколько систем счисления;

2. если соотношения оснований исходной и требуемой системы счисления – “неудобны” для непосредственных преобразований

3. если соотношения исходной и требуемой системы счисления не предполагают (исключают) непосредственные преобразования

Целесообразно коротко остановиться на каждом случае.

2 .5.1 Преобразования исходного числа в несколько систем счисления

П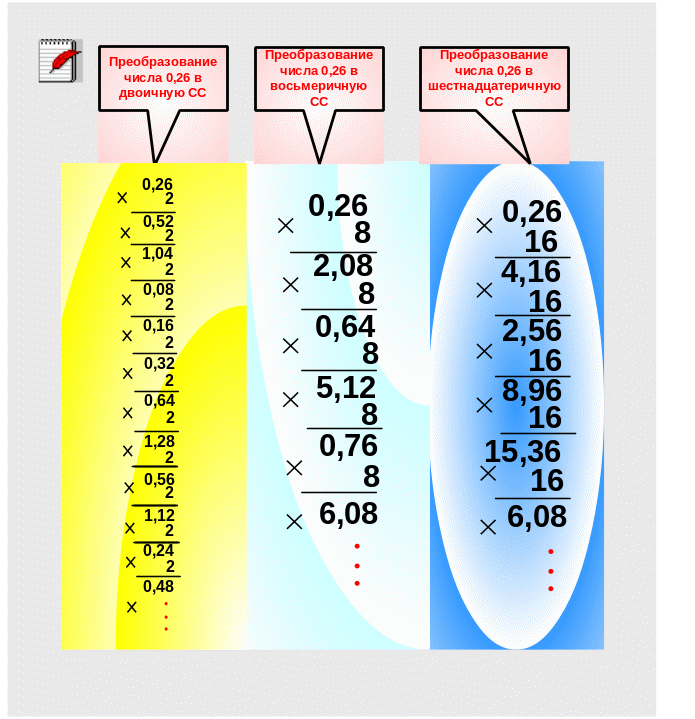 ример21 .Пусть требуется преобразовать исходное десятичное дробное число 0,26 в несколько систем счисления, например X10 → XB; X10 → Xq, X10 → Xh. . Указанные преобразования могут быть выполнены раздельно методом последовательного умножения (“цифра за цифрой” – раздел 3) .

Результаты преобразования

0,26D = 0,01000010100B = 0,20506Q=0,428F6H.

Очевидно, что затруднения (однако, не принципиальные) могут вызвать процедуры умножения дробного числа на основания 8 и 16.

Поэтому, в рамках условий примера более оптимальным является следующее поэтапное решение

1. преобразование десятичного числа в двоичную систему счисления;

2. преобразования полученного двоичного числа в восьмеричную и шестнадцатеричную системы счисления.

Для реализации второго этапа может быть применен метод подстановки с учетом специфических соотношений оснований исходной и требуемой систем счисления (раздел 2.4).

Разбиение двоичного числа на триады (тетрады) с последующей подстановкой цифр из соответствующих таблиц, менее трудоемка по сравнению с процедурой последовательного умножения на основания 8 и 16..

2.5.2 Преобразования исходного числа в “неудобную” систему счисления

Примером таких преобразований являются:

1. преобразования из восьмеричной системы счисления в шестнадцатеричную систему счисления;

2. обратные преобразования – из шестнадцатеричной системы счисления в восьмеричную систему счисления.

Использование рассмотренных ранее методов, хотя и возможно, однако, трудоемко. Например, деление по правилам восьмеричной системы счисления целого числа на шестнадцатеричное основание – неудобно, умножение дробного числа – тем более и т.д.

Более предпочтительным является использование промежуточной двоичной СС. Преобразования в этих случаях выполняются по схемам X₈ → X₂ →X₁₆; X₁₆→ X₂→ X₈.

Получение двоичного числа и дальнейшие преобразования выполняются методами взаимной замены триад (тетрад) цифрами восьмеричной (шестнадцатеричной ) систем счисления.

В качестве промежуточной может быть использована и десятичная система счисления X₈ → X₁₀ →X₁₆; X₁₆→ X₁₀→ X₈. Поэтапное решение в этом случае требует другого набора методов.