
Усе
.pdf
r z c2 x c1 y f3 .
Формулами (12), (18) і (23) записані сім перших інтегралів рівнянь незбуреного руху ШСЗ – три інтеграли площ, три інтеграли Лапласа та інтеграл енергії. Вони не можуть бути загальним розв’язком тому, що не містять явно час і не є незалежними.
Існує залежність між інтегралами площ і Лапласа, яка виражається наступним рівнянням:
f c 0 , |
(24) |
яке свідчить про ортогональність (перпендикулярність) цих двох векторів. Усі сім сталих зв’язує інше рівняння
f 2 2 hc2 , |
(25) |
де
f f 2 |
f 2 |
f 2 |
; |
c c2 |
c2 |
c2 . |
1 |
2 |
3 |
|
1 |
2 |
3 |
Дослідження незбуреного руху. Якщо векторне рівняння інтегралу площ
(10) скалярно помножити на вектор r і здійснити перетворення, отримаємо вираз
r c 0 , |
(26) |
яке виявляється рівнянням площини, що проходить через початок координат. В
координатній формі воно має такий вид:
c1x c2 y c3 z 0 . |
(27) |
Рівняння (26) або (27) показує, що незбурений рух супутника відбувається у незмінній площині, яка визначається тільки початковими умовами задачі і, як наслідок, орбіта ШСЗ є плоскою кривою. Звідси, незбурений рух відбувається у площині, яка перпендикулярна (ортогональна) до вектора площ с. З математики відомо, що положення площини у просторі визначається перпендикулярним
(ортогональним) до неї вектором. Таким чином, вектор площ с визначає орієнтацію площини орбіти супутника у просторі.
Тепер на вектор r помножимо скалярно вектор Лапласа (22), зробимо
перетворення і отримаємо таке рівняння:
r c2 f r , |
|
|
(28) |
||
а у координатній формі воно має такий вид: |
|
|
|
|
|
r c2 f x f |
2 |
y f |
3 |
z . |
(28 ) |
1 |
|
|
|
||
Рівняння (28) або (28 ) описує поверхню, на якій знаходиться супутник під час руху. Ця поверхня є поверхнею другого порядку, утвореною обертанням навколо осі, яка задана вектором f, один з фокусів якої співпадає з початком координат. Це може бути еліпсоїд, параболоїд або гіперболоїд обертання.
Розв’язок системи складеної з рівнянь (27) і (28 )
c1x c2 y c3 z 0 |
|
r c2 |
(29) |
f1x f2 y f3 z 0 |
|
геометрично є січення поверхні обертання площиною. В результаті січення виходить плоска крива другого порядку.
Згідно з першим законом Кеплера, незбурена орбіта супутника є плоскою кривою другого порядку, в одному з фокусів якої знаходиться центральне тіло
(для штучних супутників Землі центральним тілом є Земля). В залежності від ексцентриситету орбіта супутника може приймати форму однієї з наступних
плоских кривих другого порядку: |
|
||
- кола, якщо ексцентриситет |
е = 0; |
||
- еліпса, |
- « - |
0 |
< е < 1; |
- параболи |
- « - |
|
е = 1; |
- гіперболи |
- « - |
|
е > 1. |
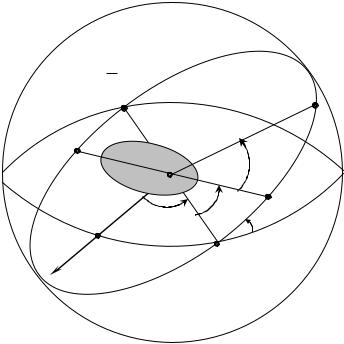
Найчастіше орбіта ШСЗ є еліпсом. У цьому випадку форма, розміри,
орієнтація орбіти супутника визначається 6-ма параметрами (елементами орбіти), а саме :
a - велика піввісь орбіти, e - ексцентриситет орбіти,
Ω - довгота висхідного вузла орбіти, i - кут нахилу орбіти,
ω - аргумент перицентру,
- момент проходження через перицентр.
|
|
|
|
|
|
|
|
A |
|
|
v |
|
|
|
П |
|
|
|
|
x |
J2000.0 |
|
|
|
|
|
Рис. 1. Елементи орбіти.
Розміри і форма орбіти задаються великою піввіссю а та ексцентриситетом
е орбіти. Орієнтація площини орбіти в просторі визначається довготою висхідного вузла орбіти Ω і кутом нахилу i.
Орбіта супутника перетинає небесний екватор у двох точках. Ці точки називаються вузлами:
-висхідний, в якому супутник перетинає екватор рухаючись з південної півкулі в північну;
-низхідний, в якому ШСЗ перетинає екватор рухаючись з північної півкулі в південну.
Довгота висхідного вузла орбіти вимірюється від точки весняного рівнодення по екватору від 0 до 360 , а кут нахилу і від площини екватора зі
сходу на захід через точку півночі від 0 до 180 . |
|
|
Аргумент перицентру (для ШСЗ - перигею) |
ω орієнтує велику вісь орбіти |
|
(лінію апсид, що з’єднує точки а п о г е ю |
і |
п е р и г е ю) в її площині, і |
вимірюється від точки висхідного вузла по |
орбіті від 0 до 360 . Апогей є |
|
найвіддаленішою точкою орбіти від Землі, а перигей – найближчою.
Положення супутника на орбіті визначається кутовим параметром v -
істинною аномалією – кутом між напрямом на перигей і на положення супутника
(див. рис. 1).
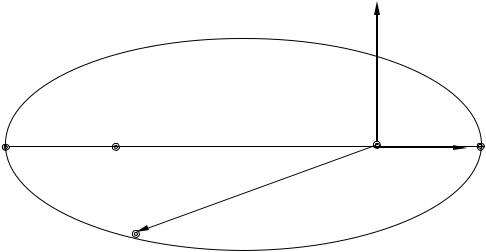
Пряма, що з’єднує фокуси, тобто лінія апсид, співпадає з напрямком вектора Лапласа, а вектор площ перпендикулярний до площини орбіти (рис. 2).
c
F2 |
F1 |
A |
П |
|
f |
|
r |
m |
|
Рис. 2. Орбіта ШСЗ із взаємним розміщенням векторів r, c і f.
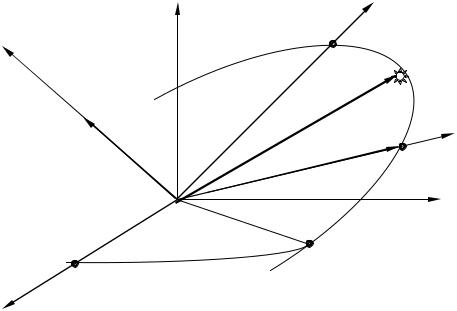
Рух супутника на орбіті визначається другим і третім законами Кеплера. У
другому законі Кеплера зазначається, що за рівні проміжки часу радіус-вектор супутника описує площі рівних секторів. Інакше кажучи, що секторіальна швидкість супутника є стала. Це можна довести, якщо розглядати рух ШСЗ у системі координат O , жорстко скріпленій з площиною орбіти (рис. 3). Дві осі,
О і O лежать у площині орбіти, тоді третя O – направлена перпендикулярно до площини орбіти по вектору інтеграла площ с. Вісь О направлена у точку перигею.
z |
|
|
c |
r |
|
|
|
|
|
|
f |
|
|
П |
|
O |
y |
|
|
|
|
|
N |
x
Рис. 3. Зв’язок систем координат O і Oxyz.
У вибраній орбітальній системі координат (рис. 3) інтеграли площ
отримаємо з виразу
i |
j |
k |
|
|
|
||
|
|
|
|
|
|
|
|
r r |
|
|
0 |
|
i 0 j 0 k c |
, |
(30) |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
||
де i , j , k - орти відповідних осей орбітальної системи координат. Розкриваючи визначник і прирівнюючи вирази при однакових ортах, отримаємо
c . |
(31) |
|
|
Введемо полярну систему координат у площині орбіти через радіус-вектор r
і кут v, і в цій системі координат виразимо інтеграл площ (31). Для цього
знайдемо вирази для координат |
, |
і складових вектора швидкості |
|
, |
|
|
|
|
|
супутника у площині орбіти |
|
|
|
|
r cos v , |
|
r cosv r sin v v , |
|
|
|
|
|
|
|
r sin v , |
|
r sin v r cos v v . |
|
(32) |
Тепер підставимо вирази (32) у формулу (31) для вектора площ і після перетворень отримаємо
r 2 v c . |
(33) |
Нехай положення супутника за невеликий проміжок часу t зміниться на кут v. Тоді площа, яку опише радіус-вектор супутника, буде площею сектора
|
s |
r 2 |
v . |
|
||||||||
|
|
2 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|||
Похідну від площі по часу t називають секторіальною швидкістю, яка |
||||||||||||
запишеться так |
|
|
|
|
|
|
|
|
|
|
|
|
s |
ds |
|
|
1 |
|
r |
2 |
v . |
(34) |
|||
dt |
|
2 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|||
Порівнюючи формули (33) і (34), маємо |
|
|
|
|
|
|
|
|
|
|||
|
s |
c |
|
, |
|
|
|
(35) |
||||
|
|
|
|
|
|
|||||||
|
|
2 |
|
|
|
|
|
|
|
|
||
що виражає другий закон Кеплера.
Рівняння орбіти в полярних координатах. Розв’язок системи рівнянь (29)
єрівнянням орбіти. В орбітальній системі координат система (29)
перетворюється у таку:

0 |
|
. (36)
r c2 f 0
Вполярних координатах друге рівняння системи (36) після підстановки
r cos v прийме вид
|
|
c 2 |
|
|
||
r |
|
|
|
|
. |
|
1 f |
cos v |
|
||||
Якщо позначити |
|
|
|
|
||
c2 p ; |
|
f e , |
(37) |
|||
отримаємо рівняння кривої другого порядку у полярних координатах |
|
|||||
r |
p |
|
, |
(38) |
||
|
||||||
1 e cos v |
||||||
де p – параметр кривої, е – ексцентриситет. Параметр орбіти (для еліптичного руху – фокальний параметр) можна виразити через велику піввісь орбіти
p a 1 e2 . |
(39) |
В залежності від ексцентриситету е плоска крива другого порядку може приймати різну форму і значення інтегралів c, f i h при цьому також змінюються. Дослідимо, які значення приймає інтеграл енергії V 2 2  r h при різних ексцентриситетах е. Для цього використаємо рівняння зв’язку перших семи інтегралів (25), в якому враховуючи позначення (37), отримаємо
r h при різних ексцентриситетах е. Для цього використаємо рівняння зв’язку перших семи інтегралів (25), в якому враховуючи позначення (37), отримаємо
e2 1 h c 2 . |
(40) |
В еліптичному русі 0 e 1, тоді на основі (40) h 0 , і з інтегралу енергії виходить, що
V 2 2 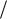 r .
r .
Це означає, що кінетична енергія руху супутника менша за його потенціальну енергію. Для окремого випадку, коли e 0 , із (40) маємо

h |
. |
(41) |
|
p |
|
При коловому русі радіус орбіти r p a . Враховуючи це і підставляючи
(41) в інтеграл енергії, отримаємо
|
|
|
|
|
|
|
|
V |
|
. |
(42) |
||||
|
|
|
r |
|
|||
Якщо приймемо, що Земля сферичної форми з радіусом 6371,1 км |
і = |
||||||
398600,5 км3/с2, то V = 7,91 км/с. |
|
|
|
|
|
|
|
При параболічному русі e 1, тому h 0 і, відповідно |
|
||||||
|
|
|
|
|
|
||
V |
2 |
. |
(43) |
||||
|
|||||||
|
|
|
r |
|
|||
Таким чином, при параболічному русі кінетична і потенціальна енергії супутника однакові. Для Землі це відбудеться при швидкості супутника то V = 11,2 км/с.
В теорії руху ШСЗ прийнято колову швидкість супутника називати першою
космічною швидкістю, а параболічну – другою космічною швидкістю.
При гіперболічному русі e 1 і h 0 , тому |
|
V 2 2 r . |
(44) |
В цьому випадку визначальну роль відіграє кінетична енергія супутника, вона більша від потенціальної енергії.
Динамічний інтеграл. Всі, отримані вище, інтеграли (12), (18) і (23) не можуть бути загальним розв’язком системи диференціальних рівнянь незбуреного руху (6), тому що не містять час у явному виді. Інтеграл, який дає в явному виді залежність положення ШСЗ на орбіті від часу t отримаємо інтегруванням виразу для інтеграла площ (33), підставляючи туди рівняння
орбітальної кривої (38), маємо
v |
dv |
|
|
|
|
|
|
|
|
|
|
|
|
t . |
(45) |
||
|
|
|
|
|||||
1 e cos v |
2 |
3 |
||||||
0 |
|
|
|
p |
|
|||

Інтеграл в лівій частині виразу (45) залежить від того, яке значення приймає ексцентриситет орбіти е.
Оскільки ШСЗ, як правило, має еліптичну орбіту 0 e 1, тому розглянемо тільки цей випадок. Для обчислення інтеграла (45) вводять нову змінну на основі тангенса половинного кута за формулою
tg |
v |
|
1 e |
|
tg |
E |
. |
(46) |
|
|
|
|
|
||||||
2 |
|
1 e |
|
|
2 |
|
|
||
Після диференціювання (46), підстановки у (45) і інтегрування отримаємо
|
|
|
|
|
|
|
|
|
||
E e sin E |
|
|
|
|
|
|
t |
. |
(47) |
|
|
|
a3 |
||||||||
Введемо середній рух n і середню аномалію M за формулами |
|
|||||||||
|
|
|
|
|
|
|||||
n |
|
|
|
|||||||
|
, |
|
(48) |
|||||||
a3 |
|
|||||||||
M n t . |
|
(49) |
||||||||
Рівняння (47) із врахуванням (48) і (49) прийме вид: |
|
|||||||||
E e sin E M . |
|
(50) |
||||||||
Це рівняння називається рівнянням Кеплера. Воно зв’язує допоміжну змінну,
якою є ексцентрична аномалія Е, середню аномалію М, момент проходження супутника через перигей і час t.
Згідно з формулою (49) середня аномалія М зростає прямо пропорціонально часові і визначає положення деякого фіктивного супутника, який рухається рівномірно по колу радіуса великої півосі а з періодом T, що дорівнює реальному.
Реальний супутник рухається по еліпсу і відповідно з другим законом Кеплера має максимальну швидкість в перигеї і мінімальну в апогеї.
Нехай супутник має період обертання Т. Тоді з рівнянь (49) і (50) виходить ,
що при повному оберті ШСЗ отримаємо 360 nT , звідси
n |
360 |
|
2 |
. |
(51) |
|
|
||||
|
T |
|
T |
|
|
Таким чином, n – середня кутова швидкість рухомої точки. В небесній механіці її називають середнім рухом.
Підставимо у формулу (51) замість n вираз (48) і після перетворень отримаємо
T 2 |
|
4 |
2 |
const , |
(52) |
a3 |
|
|
|||
|
|
|
|
Ця формула відображає третій закон Кеплера, згідно з яким в еліптичному незбуреному русі відношення квадрата періоду Т обертання супутника по орбіті до куба її великої півосі а є величина стала для даної планети.
Рух ШСЗ за законами Кеплера є найпростішою моделлю орбітального руху супутника і називається кеплерівським або незбуреним рухом. Необхідною умовою виконання законів Кеплера є припущення, що Земля (центральне тіло) і
супутник - це матеріальні точки з масами рівними масам Землі і супутника відповідно. У цьому випадку супутник рухається під дією тільки двох сил -
гравітаційного притягання Землі та прискорення супутника.
Зміст роботи
Згідно в зазначеним вище, за модель Землі приймаємо кулю з середнім радіусом R = 6371.1 км і геоцентричною гравітаційною сталою = 398600.5
км3/с2. Ці параметри є вихідними для розв’язування задач.
Задача 1. Побудувати схематично еліптичну орбіту та її проєкцію на небесну сферу за такими параметрами:
-довготою висхідного, вузла орбіти ;
-кутом нахилу орбіти і;
-аргументом перицентру
