
- •Б. 2 в. 1 Необходимые условия экстремума функции нескольких переменных. Достаточные условия
- •Почленное интегрирование и дифференцирование функциональных рядов.
- •4.Формула Тейлора с остаточным членом в форме Лагранжа. Разложение элементарных функций.
- •Б.2 в. 5 Ряд Лорана. Классификация изолированных особых точек. Вычеты.
- •8 Теорем Рисса о представлении линейного функционала
- •Теорема
- •9 Сопряженный дифф оператор
- •10. Метод малого параметра.
- •13 Задача Штурма –Лиувилля
- •Б.2 в. 14 Корректность постановки задач математической физики. Привести пример.
- •Дифференциальным уравнением называется уравнение, содержащие производные неизвестных функций.
- •Б.2 в. 16 Первая краевая задача для Ур колебания струны. Интеграл энергии и единственности решения первой краевой задачи.
- •Б.2 в. 17 Принцип максимума для уравнения теплопроводности. Единственность решения первой краевой задачи и задачи Коши.
- •Б.2 в.18 Постановка внешних и внутренних краевых задач для уравнения Лапласа. Условие разрешимости внутренней задачи Неймана.
- •Б.2 в.19 Функция Грина. Функция Грина для внутренней задачи Дирихле.
8 Теорем Рисса о представлении линейного функционала
Теорема
Пусть Н-гильбертово
пространство (комплексное или вещественное)
Для любого линейного ограниченного
функционала f заданного всюду на Н
существует единственный элемент
![]() такой
что для всех
такой
что для всех
![]()
![]()
При этом ||f||=||y||
Доказательство
Рассмотрим L
–множество всех элементов
![]() таких
что
таких
что
![]()
Если L=H то f=0 можно взять y=0 и теорема доказана
Пусть
![]() тогда найдется
тогда найдется
![]() причем можно считать что <z_0,f>=1
Пусть теперь
причем можно считать что <z_0,f>=1
Пусть теперь
![]() тогда
x-<x,f>z_0
тогда
x-<x,f>z_0![]() так как
так как
![]()
Следовательно
![]() откуда
откуда
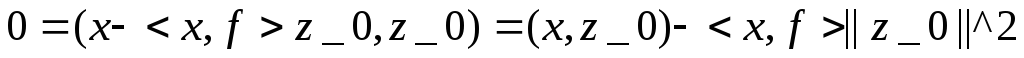
отсюда
![]() Итак можно принять
Итак можно принять
![]()
Покажем что ||f||=||y|| Действительно
![]()
По неравенству
Коши-Буняковского Из определения нормы
f
имеем
![]() Но
кроме того
Но
кроме того
![]()
Откуда
![]() Итак
||f||=||y||
Итак
||f||=||y||
Осталось доказать
единственность y.
Если
![]() то
то
![]() для
любых
для
любых
![]() Возьмем
Возьмем
![]() и получим
и получим
![]() ЧТД
ЧТД
9 Сопряженный дифф оператор
Пусть дан оператор L
![]()
![]()
Дифф оператор L* называется сопряженным к оператору L если он порожден сопряженным дифф выражением l*(y) и сопряженными краевыми условиями V_1=0,V_2=0,…,V_(2n-m)=0
Для нахождения сопряженного дифф уравнения используем
интегрирование по частям
получим
![]()
![]()
Это формула Лагранжа. Где -билинейная форма
![]()
![]()
![]()
Для нахождения
сопряженных краевых условий выразим
![]()
Из условий
![]()
Если необходимо то дополним эту систему линейно независимыми для остальных y-ов
П![]() одставим
эти выражения в билинейную форму
одставим
эти выражения в билинейную форму
И обозначим
коэффициенты перед
![]()
Через
![]()
Тогда формула Лагранжа перепишется
![]()
ВПОЛНЕ НЕПРЕРЫВНЫЕ ОПЕРАТОРЫ
Опр Оператор
![]() называется вполне непрерывным (или
компактным) если замкнутый единичный
шар пространства Х он переводит в
компактное множество пространства Y
называется вполне непрерывным (или
компактным) если замкнутый единичный
шар пространства Х он переводит в
компактное множество пространства Y
Не всякий оператор
из L(X,Y)
является вполне непрерывным. Напимер
![]() не является если Х не конечномерно т.к.
единичный шар в Х
не является если Х не конечномерно т.к.
единичный шар в Х
![]() является компактным множеством в Х лишь
в случае конечномерности Х.
является компактным множеством в Х лишь
в случае конечномерности Х.
Свойство
Если
![]() вполне непрерывен то любое ограниченное
в Х множество он переводит во множество
компактное в Y.
вполне непрерывен то любое ограниченное
в Х множество он переводит во множество
компактное в Y.
Доказательство
Пусть
![]() и М ограничено т.е. существует R>0
такое что ||x||<=R
для любых
и М ограничено т.е. существует R>0
такое что ||x||<=R
для любых
![]() Возьмем любую последовательность
Возьмем любую последовательность
![]() тогда
y_n=Ax_n
де х_n
тогда
y_n=Ax_n
де х_n![]() Рассмотрим
Рассмотрим
![]() -единичный
шар в Х. Вследствие полой непрерывности
-единичный
шар в Х. Вследствие полой непрерывности
![]() содержит
фундаментальную подпоследовательность
содержит
фундаментальную подпоследовательность![]() .Но
тогда и
.Но
тогда и
![]() фундаментальная
подпоследовательность последовательности
{y_n}
т.е. AM
компактно
фундаментальная
подпоследовательность последовательности
{y_n}
т.е. AM
компактно
10. Метод малого параметра.
Рассм-м систему
диф ур-й
![]() с
нач-ми усл-ми
с
нач-ми усл-ми
![]() (1)
(1)
Пусть fi
и ai
явл-ся аналитич-ми ф-ми по совок-ти
переем-х![]() ,тогда
вектор-решение этой системы
,тогда
вектор-решение этой системы
![]() разлагается
в сходящийся при малом μ ряд:
разлагается
в сходящийся при малом μ ряд:
![]() =
=
=![]() Для
поиска фун-й
Для
поиска фун-й
![]() надо
разложить правую часть сист(2),приравняв
коэф-ты при при одинак-х степенях μ.В
рез-те получим сист диф-х ур-й с соотв-ми
нач-ми усл-ми,интегрируя кот послед-но
найдем ф-ии
надо
разложить правую часть сист(2),приравняв
коэф-ты при при одинак-х степенях μ.В
рез-те получим сист диф-х ур-й с соотв-ми
нач-ми усл-ми,интегрируя кот послед-но
найдем ф-ии
![]() Пользуясь
мтодом малого пар-ра можно находить
периодич-ие решения:
Пользуясь
мтодом малого пар-ра можно находить
периодич-ие решения:![]() ,
(3)
,
(3)
гдеF-известная
периодич. ф-я по f.В
этом случае константы возник-ие при
интегрир-ии сис диф-ых ур-й,находятся
из условий нормы,заключ в отсутствии
резонирующих слагаемых в пр-й части.Если
ф-ия зав-т от t,то
период решения
x(t,μ)
заранее неизвестен.В этом случае замена
вида:![]() (4),где
τ-новая неиз-ая перем-ая и искать решение
x(t,μ).При
этом коэф-ты b1,b2,…опред-ся
из усл-й период-ти решений ур-ия (2)
(4),где
τ-новая неиз-ая перем-ая и искать решение
x(t,μ).При
этом коэф-ты b1,b2,…опред-ся
из усл-й период-ти решений ур-ия (2)
у0(τ),….
11.Рез-ое множ-во и спектр линейного оператора.
Пусть Х компл-ое
банахово простр-во.Рассм-м опер-р А:Х![]() Х
с обл-ю опред-я D(A)
плотной в Х.Теперь рассм опер-р A-λI,где
λ компл-ое число,I
единица в L(Х).
Х
с обл-ю опред-я D(A)
плотной в Х.Теперь рассм опер-р A-λI,где
λ компл-ое число,I
единица в L(Х).
Опр1Точка
λ наз-ся регулярной точкой оператора
А,если опер-р A-λI
непрер-но обратим.Совок-ть регул-х точек
опер-ра А наз-ся резольвентным множ-ом
опер-ра А и обознач-т ρ(А).Если λ![]() ρ(А),то
лин-й опер-р Rλ=
(A-λI)-1
наз-ся резольвентой опер-ра А.
ρ(А),то
лин-й опер-р Rλ=
(A-λI)-1
наз-ся резольвентой опер-ра А.
Т1 Резольвентное мн-во ρ(А) всегда открыто.
Док-во
Пусть λ0![]() ρ(А).Это
означает,чтоопер-р А- λ0I
непрер-но обратим.Рассм-м опер-р A-λI
и запишем тождество: A-λI=
А- λ0I-(λ-
λ0)I=(
А- λ0I)[I-(
λ- λ0)I((A-λI)-1]=(
А- λ0I)[I-(
λ- λ0)I
R
ρ(А).Это
означает,чтоопер-р А- λ0I
непрер-но обратим.Рассм-м опер-р A-λI
и запишем тождество: A-λI=
А- λ0I-(λ-
λ0)I=(
А- λ0I)[I-(
λ- λ0)I((A-λI)-1]=(
А- λ0I)[I-(
λ- λ0)I
R![]() (A)]=(
А- λ0I)
[I-(
λ- λ0)
R
(A)]=(
А- λ0I)
[I-(
λ- λ0)
R![]() (A)](1)Поскольку
опр-р А- λ0I
непрер обратим,то опер-р A-λI
будет непрер обратим
(A)](1)Поскольку
опр-р А- λ0I
непрер обратим,то опер-р A-λI
будет непрер обратим![]() когда
непрер обратим будет опер-р I-(
λ- λ0)
R
когда
непрер обратим будет опер-р I-(
λ- λ0)
R![]() (A).Воспольз
теор-й об обратном операторе.Согласно
этой теореме опер-р I-(
λ- λ0)
R
(A).Воспольз
теор-й об обратном операторе.Согласно
этой теореме опер-р I-(
λ- λ0)
R![]() (A)
будет непрер обратим,если |λ- λ0|
||R
(A)
будет непрер обратим,если |λ- λ0|
||R![]() (A)||<1
(A)||<1![]() если
λ0
если
λ0![]() ρ(А),то
круг Sr(λ0),где
ρ(А),то
круг Sr(λ0),где
![]() тоже лежит в ρ(А).А это означает,что ρ(А)
открытое множ-во.
тоже лежит в ρ(А).А это означает,что ρ(А)
открытое множ-во.
Т2
Пусть А![]() L(Х),тогда
{λ:|λ|>||A||}
L(Х),тогда
{λ:|λ|>||A||}![]() ρ(А).
ρ(А).
След-е.Если
опер.![]() огр-н,то
мн-во
огр-н,то
мн-во
![]() неогр.
неогр.
Опр2.Дополнение
к![]() в
компл.плоскости наз.спектром опер.
в
компл.плоскости наз.спектром опер.![]() и обозн.
и обозн.![]()
Из теор.1![]() ,что
спектр любого линейного опер-ра
Aявл.замкн.мн-ом(как
дополн.к открытому мн-ву)
,что
спектр любого линейного опер-ра
Aявл.замкн.мн-ом(как
дополн.к открытому мн-ву)
Из теор.2![]() ,что
спектр огран. лин. опер-ра Aлежит
в круге
,что
спектр огран. лин. опер-ра Aлежит
в круге
![]() и
и
![]() явл.огр-м
мн-ом.
явл.огр-м
мн-ом.
Если![]() то
возм.
то
возм.![]() 3
случая:
3
случая:
1)опер![]() необратим;2)опер
необратим;2)опер![]() обратим,но
его обл.знач-ий
обратим,но
его обл.знач-ий![]()
![]()
![]()
3) опер![]() обратим,
обратим,
![]()
![]()
![]() но
опер-р
но
опер-р![]() -1неогр.
-1неогр.
Замеч-е Из
теор-ы Банаха об обратном опер-ре![]() ,что
случай3)не возможен,если D(A)=Х
и опр-р А огр-н.
,что
случай3)не возможен,если D(A)=Х
и опр-р А огр-н.
Среди точек спектра
![]() важную
роль играют собств-ые значения опер-ра
А.Если λ-собств значен опер-ра А,то имеет
место первый случай(оператор
важную
роль играют собств-ые значения опер-ра
А.Если λ-собств значен опер-ра А,то имеет
место первый случай(оператор![]() необратим).В
этом случае
необратим).В
этом случае![]() х=0,где
х-собст-ый вектор,отвеч λ,но тогда мн-во
нулей N
х=0,где
х-собст-ый вектор,отвеч λ,но тогда мн-во
нулей N![]() ≠{0}
≠{0}
![]() опер-р
опер-р
![]() -1не
сущ-ет.
-1не
сущ-ет.
Пример1 Если пр-во Х конечномерно,то спектр любого линейного опер-ра сост только из собст-ых значений.В m-мерном евкл-м или унитарном пр-ве Х всякий самосопр-ый опер-р имеет ровно m собств-ых значений с учетом их кратности.
Пример2
Спектр![]() всякого вполне непрер опер-ра
бесконечноммерно в банах-м пр-ве Х сост
из не более,чем счетного мн-ва собств-ых
значений,единой предельной тоской кот
может служить точка λ=0.
всякого вполне непрер опер-ра
бесконечноммерно в банах-м пр-ве Х сост
из не более,чем счетного мн-ва собств-ых
значений,единой предельной тоской кот
может служить точка λ=0.
№12 Задачу,определ-ую частные решения диф-го уравнения,удовл-го заданным условиям будем называть краевой задачей.
Рассмотрим краевые
задачи на отр [0,l]
оси Ох для лин-го диф-го ур-ия 2го пор-ка
![]() ,где
g(x),h(x),f(x)-непрер
ф-ии на [0,l].
,где
g(x),h(x),f(x)-непрер
ф-ии на [0,l].
Введем ф-ю
![]() заметим,что
заметим,что
![]() Через
L[y]=f(x).Выр-ие
L[y]
наз диф-ым опер-м.Рассм краевую задачу
для лин-го диф-го ур-ия 2го пор-ка,которое
сведено к изучению краевых задач для
ур-ия L[y]=f(x).Краевая
задача L[y]=f(x)
рассм с лин граничн усл-ми вида:
Через
L[y]=f(x).Выр-ие
L[y]
наз диф-ым опер-м.Рассм краевую задачу
для лин-го диф-го ур-ия 2го пор-ка,которое
сведено к изучению краевых задач для
ур-ия L[y]=f(x).Краевая
задача L[y]=f(x)
рассм с лин граничн усл-ми вида:![]() .
.
Краевые зад,в кот пр ч ур-ие ≠0 наз-ся неоднор краевыми задачами.
Краевые задачи для однор ур-ия с однор гран усл-ми наз однородн краев задачами.
Р ассм
краевую задачу L[y]=f(x)
ассм
краевую задачу L[y]=f(x)
![]() .(1)
.(1)
Ф-ии p(x)>0 и непрер диф-ма на [0,l] ,а действ-ые ф-ии g(x) и f(x)-непрер ф-ии на отр [0,l].
Опр Реш-е краевой задачи (1) наз непрер диф-ой на [0,l] ф-ия у(х) с непрер 2й произ-ой на инт-ле [0,l],удовл на [0,l] ур-ию и гран усл-ям(1).
Предп,что сущ-ет
решение задаи (1)при спец-ом способе
зад-ия правой части ур-ия,а именно при
ф-ии f(x)
отличной от 0 лишь в ε-окр-ти некот-й фикс
точки х=ξ![]() (0,l):
(0,l):
![]()
F(x)=
![]() (2)
(2)
![]()
Причем,ф-ия fε≥0
и
![]() (3).Решение
этой задачи обозн-т уε(х,ξ).
Интегрир ур-ия(1) с таким обр зад ф-ей по
отр [ξ-ε,
ξ+ε]
получим
(3).Решение
этой задачи обозн-т уε(х,ξ).
Интегрир ур-ия(1) с таким обр зад ф-ей по
отр [ξ-ε,
ξ+ε]
получим
![]()
![]()
![]()
![]()
![]() 1(т.к.интегр=1)(4)
1(т.к.интегр=1)(4)
Предп,что предельная
ф-ия
![]() сущ-ет и непрер на [0,l],тогда
совершая пред-й переем при ε ->0 в (4)
получим,что производная
сущ-ет и непрер на [0,l],тогда
совершая пред-й переем при ε ->0 в (4)
получим,что производная
![]() в точке х=ξ должна иметь разрыв 1го
рода,причем разность пр и левого пред-го
знач-ия этой произв-ой в точке х=ξ опред
выр-м
в точке х=ξ должна иметь разрыв 1го
рода,причем разность пр и левого пред-го
знач-ия этой произв-ой в точке х=ξ опред
выр-м
![]() -
-![]() .Т.о.
если ф-ия
.Т.о.
если ф-ия
![]() сущ-ет,то
она подчин-ся след-м усл-ям:1)как ф-ия
перем-ой х
сущ-ет,то
она подчин-ся след-м усл-ям:1)как ф-ия
перем-ой х
![]() удовл однор ур-ию при 0<x<ξ,ξ<x<l;2)
удовл однор ур-ию при 0<x<ξ,ξ<x<l;2)
![]() удовл-ет
гран-м усл-ям (1);3)
удовл-ет
гран-м усл-ям (1);3)
![]() непрер
на [0,l],а
ее первая произв-ая в точке х=ξ имеет
разрыв 1го рода с велич-й скачка предельн
знач =
непрер
на [0,l],а
ее первая произв-ая в точке х=ξ имеет
разрыв 1го рода с велич-й скачка предельн
знач =![]()
ОпрФ-ию,удовл усл (1-3) наз-т функцией Грина первой краевой задачи.
Существенное
значение ф-ии Грина закл в том,что что
через нее м.б. выражено реш-е первой
краевой задачи с произв правой частью
f(x).Пусть
сущ-ет реш-е зад(1) и ф-ия Грина
![]() .Примен
форм-лу Грина
.Примен
форм-лу Грина
![]()
=![]() к этим ф-м на отр [0,ξ-ε]
и [ξ+ε,l],где
ф-ии y(x)
и
к этим ф-м на отр [0,ξ-ε]
и [ξ+ε,l],где
ф-ии y(x)
и
![]() непрер диф-мы и обл-т 2мя непрер
произв,получим
непрер диф-мы и обл-т 2мя непрер
произв,получим
![]()
+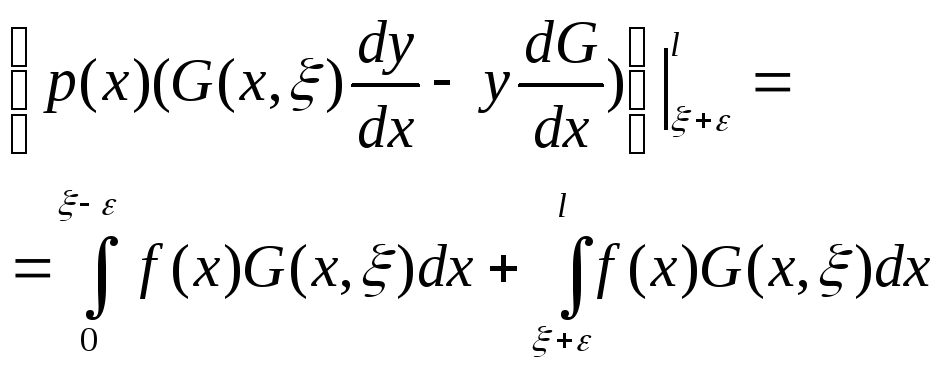 (5)
(5)
Т.к. ф-ии у(х) и
![]() удовл однородн граничн усл-я (1),то
подст-ки х=0 и х=l
обращ-т в нуль.Переходя в (5) к пределу
всилу опред ф-ии Грина получим
удовл однородн граничн усл-я (1),то
подст-ки х=0 и х=l
обращ-т в нуль.Переходя в (5) к пределу
всилу опред ф-ии Грина получим
![]() ,что
и т.д.
,что
и т.д.
