13 Задача Штурма –Лиувилля

Имеет вид

Где q(x) – действительная непрерывная функця на некотором отрезке [a,b]

произвольные действительные числа

Лемма1

Если функции положительны в каждой точке отрезка [a,b]

То функция является решением дифференциального уравнения

Тогда и только тогда, когда функция

является решением уравнения

Где

Доказательство

Если функция то и функция

И наоборот если то функция

Учитывая равенства

Получаем

Осталось воспользоваться равенством

Лемма2

Если на [a,b] то уравнение

Эквивалентно уравнению

где

Доказательство

Очевидно что

Так как

То коэффициент при равен нулю то есть

Следовательно

Б.2 в. 14 Корректность постановки задач математической физики. Привести пример.

Так как задачи мат физики представляют собой мат модели реальных физических процессов то их постановки должны удовлетворять следующим естественным требованиям: 1) решение должно существовать в каком-либо классе функций , 2) решение должно быть единственным в каком-либо классе функций , 3) решение должно непрерывно завесить от данных задачи (начальных и граничных данных, свободного члена, коэффициентов ур-ия).

Непрерывная зависимость решения u от данных задачи D означает следующее: пусть последовательность данных , k=1,2,… в каком-то смысле стремится к D , и k=1,2,… соответствующее решения задачи; тогда должно быть в смысле надлежащим образом выбранной сходимости. Например пусть задача приводится к уравнению где L – линейный оператор, переводящий M в N, где M и N – линейные нормированные пространства. В этом случае непрерывная зависимость решения u от свободного члена F будет обеспечена если оператор существует и ограничен из N в М. требование непрерывной зависимости обуславливается тем обстоятельством что физические данные как правило определяются из эксперимента приближенно и поэтому нужно быть уверенным в том что решение задачи в рамках выбранной мат модели не будет существенно зависеть от погрешностей измерений.

Задача удовлетворяющая перечисленным требованиям называется корректно поставленной (по Адамару), а множество функций наз-ся классом корректности. Задача не удовлетворяющая хотя бы одному из условий 1)-3) наз-ся некорректно поставленной.

К некорректно поставленным задачам часто приводят обратные задачи мат физики: по некоторой информации о решении прямой задачи восстановить некоторые неизвестные физические величины, определяющие эту задачу (источники, краевые условия, коэффициенты уравнения и др.).

15

Дифференциальным уравнением называется уравнение, содержащие производные неизвестных функций.

Если неизвестная функция зависит от одной переменной, то это уравнение называетсяобыкновеннвм диф ур-ем, в противном случае- ур-ем в частных производных. Наивысший порядок производных неизвестной функции, входящих в уравнение, называется порядком уравнения.

Частной производной первого порядка функции u([) по переменной х_i называется предел

Дифференциальным уравнением с частными производные относительно неизвестн функции u(x) называется отношение

Введем сокращенное обозначение , где L- дифференц оператор, действующий на функцию и преобразующий их в элементы пространства непрерывных функций .

Уравнение вида , где множеству непрерывных функций, называется линейным дифференциальным уравнением с частными производными, если для диф оператора L выполнены условия линейности

1)

2)

Рассмотри класс уравнений второго порядка с двумя неизвестными переменными. Введем специальные обозначения независ перем тогда

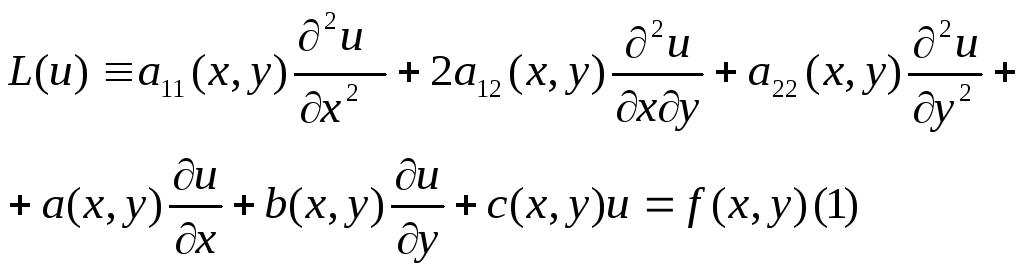
- заданные функции двух переменных

неизвестная функция

Для классификации уравнений (1), построим вспомогательную функцию

называемой дискриминантом уравнения.

Определение Тип уравнения определяется следующим образом

1) >0, то (1) называется гиперболического типа

2) <0-эллиптического типа

3) =0-параболического в точке (х,у)

Примера:

1. гиперболич тип – уравнение колебание струны 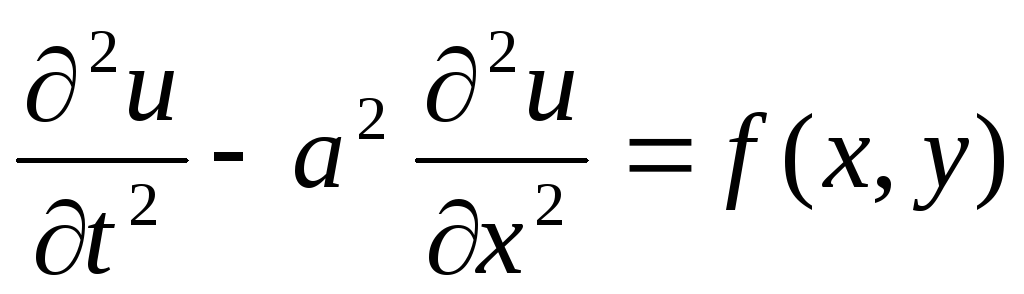, где

х=х₁пространственная переменная, t=х₂- временная переменная.

2) эллиптический тип- Уравнение Лапласа ; х,у- пространственная переменная

3) параболическое уравнение-уравнение теплопроводности

Перейдем в уравнении (1) от неизвестных переменных х, уК новым независимым переменным с помощью невырожденного преобразования

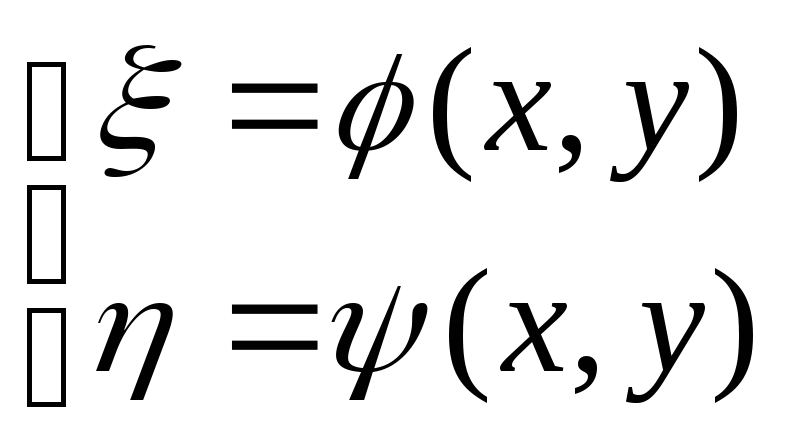(2)

Преобразование (2) называется невырожденным в Е, если якобиан

Преобразуем производные к новым переменным

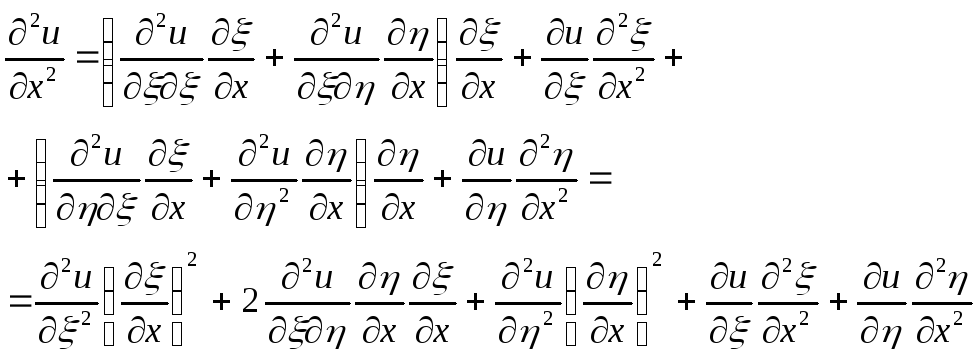
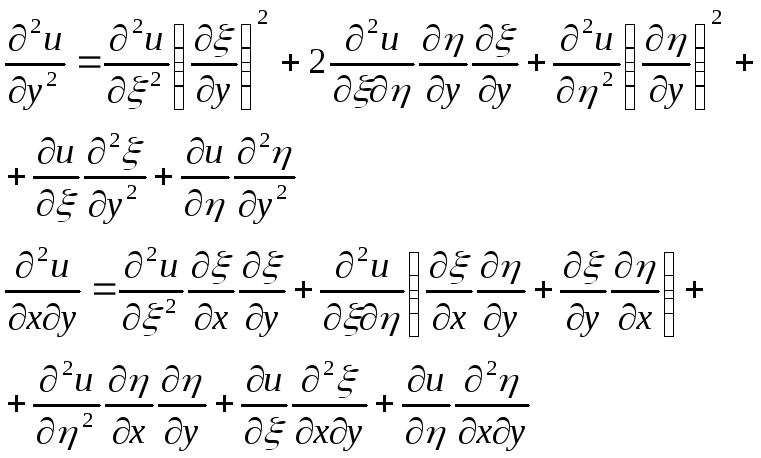(3) Подставляя значения производных из (3) в (1) будем иметь

(4)

где

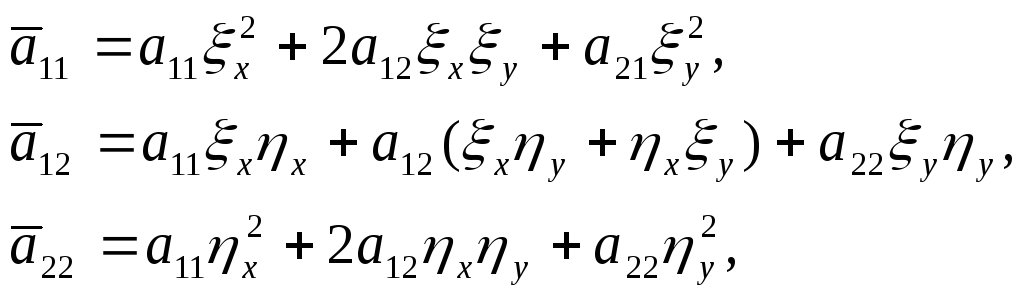
функция не зависит от вторых производных.

Выберем переменные таким образом, чтобы коэффициент был равен нулю. Рассмотрим уравнение с частн производными первого порядка

(5)

Пусть -какое нить частное решение этого уравнения. Если положить то , таким образом задача о выборе новых неизвестных переменных связана с решением уравнения (5).

Лемма: Если является частным решением уравнения , то соотношение представляет собой общий интеграл обыкновенного диф уравнения

(6)

Уравнение (6) называется характеристическим уравнением для уравнения (1), а его интегралы- характеристиками.

Уравнеине (6) распадается на 2 уравнения:

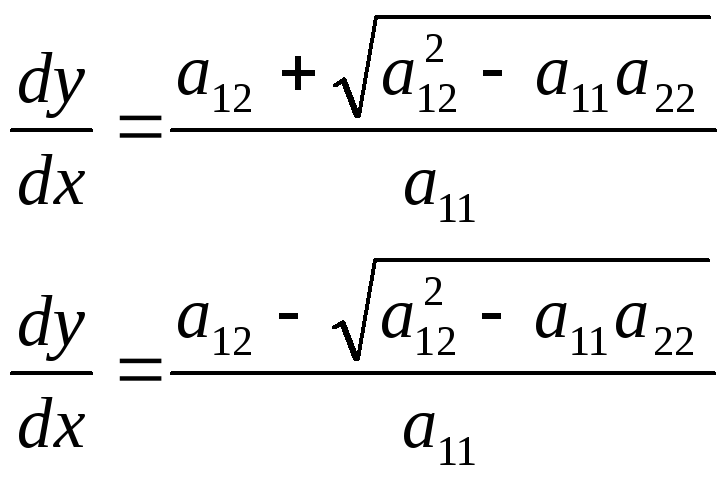
А подкоренное выражение определяет тип уравнения (1)

1) Пусть >0 (гиперболический тип)

Канонич вид тогда будет

2. Пусть 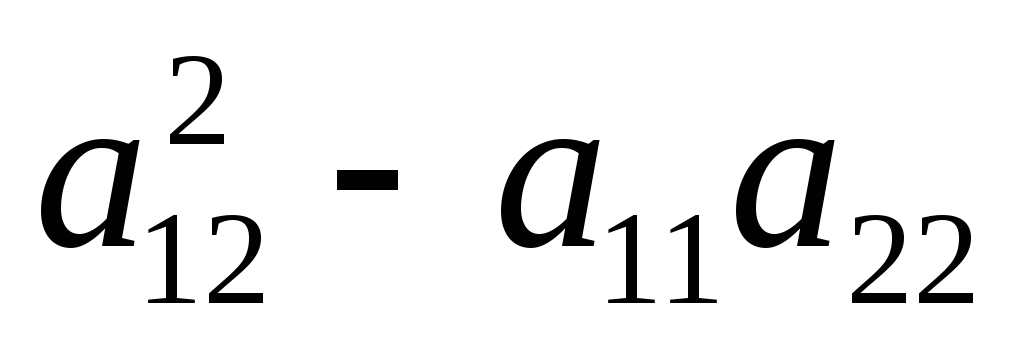=0 (параболический тип)

Канония вид

3)

Пусть <0 (элиптич тип )