Б.2 в.18 Постановка внешних и внутренних краевых задач для уравнения Лапласа. Условие разрешимости внутренней задачи Неймана.

Простейшим уравнением эллиптического типа является уравнение Лапласа: . Функция называется гармонической в конечной области D, если она в этой области имеет непрерывные производные до второго порядка и удовлетворяет уравнению Лапласа во всех точках D. Функция называется гармонической в бесконечной области D, если она в этой области имеет непрерывные производные до второго порядка, удовлетворяет уравнению Лапласа во всех точках D и равномерно стремится к нулю при стремлении точки в бесконечность (ф-ия при , если для заданного число А>0 такое что при , где r – расстояние точки М от начала координат).

Пусть S – замкнутая поверхность. Обозначим через конечную область, ограниченную этой поверхностью; через - бесконечную область внешнюю к также ограниченную поверхностью S. Пусть на поверхности S заданы непрерывные функции.

Внутренняя задача Дирихле. Найти ф-ию гармоническую в области непрерывную в замкнутой области и принимающую на поверхности S заданные значения (1)

Внешняя задача Дирихле состоит в определении функции гармонической в , непрерывной в и удовлетворяющей условию (1).

Внутренняя задача Неймана. Найти ф-ию гармоническую в области такую чтобы ее производная по направлению внешней нормали в каждой точке поверхности S равнялась значению в этой точке заданной ф-ии (2).

Внешняя задача Неймана состоит в определении гармонической в ф-ии нормальная производная которой на поверхности S удовлетворяет условию (2).

Третья краевая задача. Найти ф-ию гармоническую в области непрерывную в и такую что в каждой точке поверхности S равно значению в этой точке заданной функции , где - заданная непрерывная ф-ия на поверхности S . Аналогично формируется 3-я внешняя краевая задача.

Уравнение Лапласа в сферических координатах: .

Уравнение Лапласа в цилиндрических координатах: .

Решение внутренней задачи Неймана в D ,

существует лишь при условии . Это условие необходимо и достаточно и определено с точностью до произвольного постоянного слагаемого.

Б.2 в.19 Функция Грина. Функция Грина для внутренней задачи Дирихле.

Простейшим уравнением эллиптического типа является уравнение Лапласа: . Функция называется гармонической в конечной области D, если она в этой области имеет непрерывные производные до второго порядка и удовлетворяет уравнению Лапласа во всех точках D. Функция называется гармонической в бесконечной области D, если она в этой области имеет непрерывные производные до второго порядка, удовлетворяет уравнению Лапласа во всех точках D и равномерно стремится к нулю при стремлении точки в бесконечность (ф-ия при , если для заданного число А>0 такое что при , где r – расстояние точки М от начала координат).

Пусть - конечная область трехмерного пространства, ограниченная кусочно – гладкой ориентируемой поверхностью и пусть функции имеют внутри непрерывные и ограниченные производные первого порядка. Тогда имеет место формула Остроградского: (1), где n – внешняя нормаль к поверхности .

Выведем формулы Грина.

Пусть ф-ии и и их частные производные первого порядка непрерывны в вплоть до , частные производные второго порядка внутри непрерывны и ограничены. Полагая и пользуясь формулой (1) приходим к первой формуле Грина (2).

Меняя местами u и v в формуле (2) будем иметь (3).

Вычитая (2) из (3) получим вторую формулу Грина (4).

Лемма. Если функция непрерывна, имеет непрерывные производные первого и второго порядка везде в области , причем первые производные непрерывны вплоть до границы, а вторые производные непрерывны внутри области, то имеет место формула:

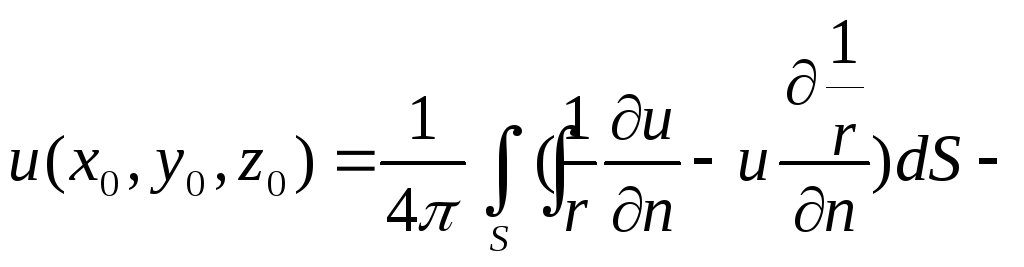
(5) где - расстояние от фиксированной точки лежащей внутри , до переменной точки , n – внешняя нормаль к поверхности .

Пусть гармоническая функция внутри конечной области - непрерывна вместе с производными первого порядка вплоть до границы области . Пусть известна ф-ия обладающая свойствами: 1) как функция переменной точки М она является гармонической внутри области и имеет непрерывные первые производные вплоть до поверхности ; 2) на поверхности ф-ия принимает граничные значения .

Функцией Грина задачи Дирихле для уравнения Лапласа называется ф-ия удовлетворяющая следующим условиям: 1) как функция точки М есть гармоническая внутри области исключая точку где она обращается в бесконечность; 2) она удовлетворяет граничному условию (6) ; 3) в области ф-ия допускает представление (7), где .

Построение ф-ии Грина сводится к нахождению ее регулярной части кот определяется из решения задачи Дирихле: ().

С помощью ф-ии Грина решение внутренней задачи Дирихле (если оно существует) дается формулой