Б. 2 в. 1 Необходимые условия экстремума функции нескольких переменных. Достаточные условия

Пусть ф-ия определена в области Д и будет внутренней точкой этой области. Говорят что ф-ия в точке имеет максимум (минимум) если ее можно окружить такой окрестностью чтобы для всех точек этой окрестности выполнялось неравенство . Если выполняется строгое неравенство то говорят что в точке имеет место собственный максимум (минимум). Для обозначения максимума и минимума используется термин экстремум.

Пусть ф-ия определена в некоторой точке . Необходимое условие существования экстремума: обращение в нуль частных производных первого порядка является н. условием существования экстремума. Итак «подозрительными» на экстремум явл. те точки в кот частные производные первого порядка все обращаются в нуль их координаты можно найти решив систему уравнений

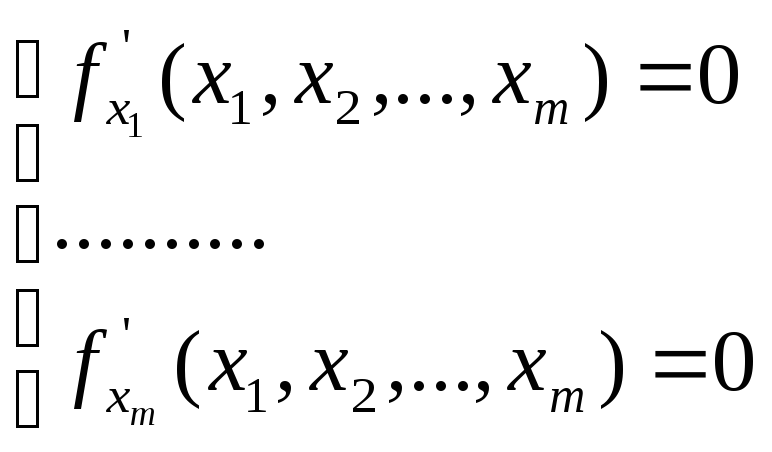
Подобные точки называются стационарными.

Достаточные условия существования экстремума. Ограничимся случаем ф-ии двух переменных . Предположим что она определена непрерывна и имеет непрерывные частные производные первого и второго порядка в окрестности некоторой точки кот явл стационарной, т.е. удовлетворяет условиям (1)

Положим . Если то в испытуемой стационарной точке ф-ия имеет экстремум: максимум при и минимум при . Если то экстремума нет. В случае для решения вопроса приходиться привлекать высшие производные. Для того чтобы найти наибольшее (наименьшее) значение ф-ии в область Д нужно найти все внутренние стационарные точки, подозрительные по экстремум вычислить значение ф-ии в них и сравнить со значениями ф-ии в пограничных точках области: наиб (наим) из этих значений и будет наиб (наим) значение ф-ий во всей области.

№2. Теорема(ф-ла Остроград) Пусть у₁=у₁(х),у₂=у₂(х) два каких-либо решения однородного диф-го уравн-я 2го порядка, тогда справедл. след-ая формула W(x)=W(x₀), где х₀,х(a,b)

Док-во

Т.к. у₁ и у₂ реш-ия ур-я у′′+p(x) у′+q(x)y=0, то у₁′′+p(x)у₁′+q(x)y₁=0, у₂′′+p(x)у₂′+q(x)y₂=0 разделим на у₁ и у₂ соотв-но и сложим,получим (у₁ у₂′′- у₁′′ y₂)+ p(x)(у₁ у₂′- у₁′ y₂)=0, у₁ у₂′′- у₁′′ y₂=W′(x), у₁ у₂′- у₁′ y₂=W(x).Действит, W′(x)=( у₁ у₂′- у₁′ y₂)′= у₁ у₂′′- у₁′′ y₂. Т.о. приходим к ур-ию: W′(x)+ p(x) W(x)=0, от явл ур-ем с раздел переем.Проинтегр обе части этого ур-ия в пром-ке от х₀ до х,где[x₀,x](a,b)после интегрир и преобраз-й получим ч и т.д.

3. Почленное интегрирование и дифференцирование функциональных рядов.

Пусть абсолютно интегрируемая функция на промежутке и пусть её ряд Фурье такой:

(1). Рассмотрим для всех функцию (2). Эта функция очевидно непрерывна и с ограниченными изменениями. Кроме того, функция имеет период . 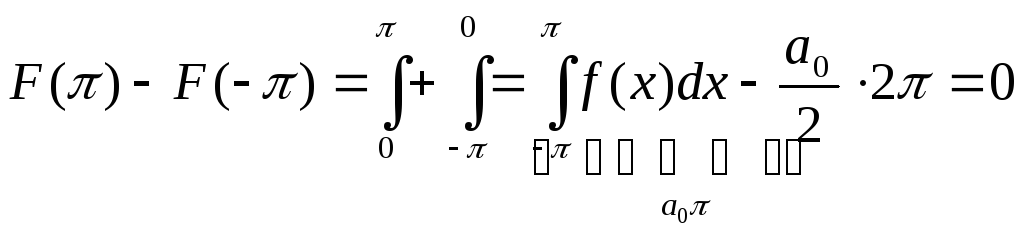(3).

В этом случае по признаку Дирихле-Жордано ф. разлагается в промежутке в ряд Фурье (4). Данный ряд по одному признаку будет равномерно сход-ся на промежутке. Между коэффициентами (1) и (4) существует некая связь. Если воспользоваться методом интегрирования по частям, то для любого

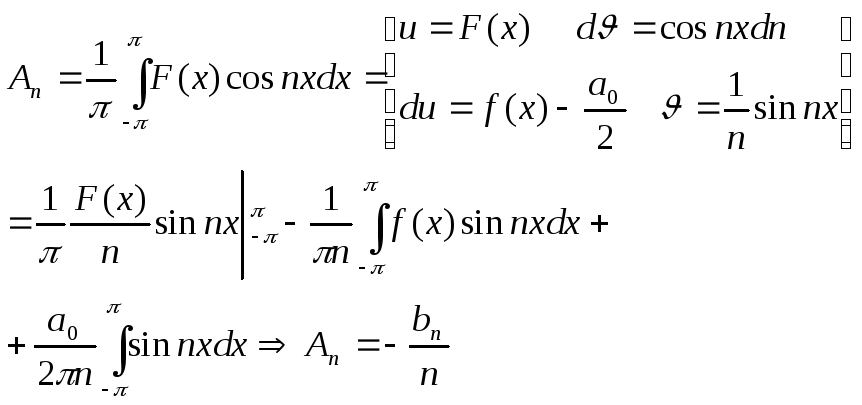
Аналогично, учитывая (3) получим . Для нахождения подставим в выраж. (4)

(5). Подставим в разложение (4) найденное значение коэффициентов, получим:

(*)

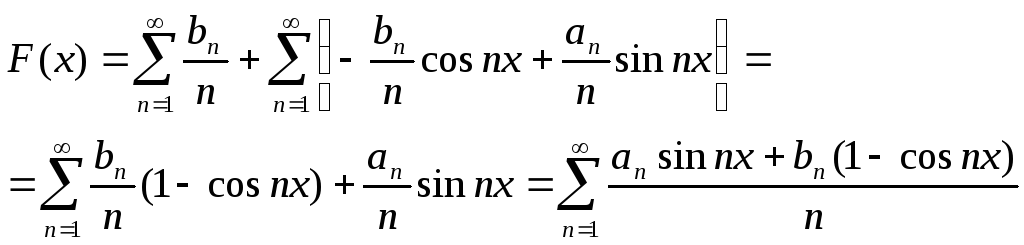Учитывая (2), получим: (6).

Очевидно, для любого отрезка имеет место соотношение подобное (6)

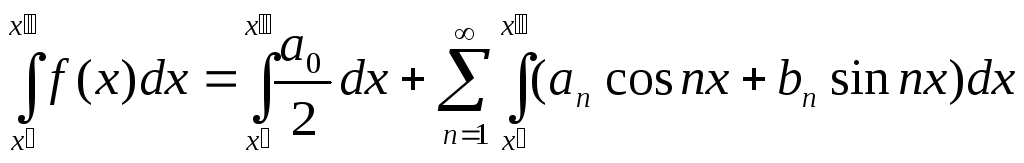. Т.о., интеграл о функции получился почленным интегрированием соответствующего ей ряда Фурье. Почленное интегрирование р.Фурье всегда допустимо, т.к. мы установили этот факт даже не делая предположение о сходимости самого ряда (1) ф-ии .

Пусть на задана ф-ия , непрерывная и удовл. Усл. , причём существует . Пусть является абсолютно интегрируемой на указанном промежутке ф-ией как выше р.Фурье (1) ф-ии получается из р.Фурье ф-ии ,

(7). Почленным интегрированием, т.к. при наложении определённых условий в выраж.(7) свободного члена не будет: . Очевидно, что и обратно ряд (7) для ф-ии может быть получен из (1) для ф-ии почленным дифференцированием. Заметим, что большую роль грает предположение о периодичности . При нарушении этого условия свободный член р.Фурье ф-ии был бы отличен от нуля упомянутый ряд не мог бы быть получен из (1) почленным дифференцированием. Отметим, что при дифф-ии и появляются множители ; порядок малости коэф-ов понижается и ухудшаются шансы на сходимость, например в случае разложения почленное дифф-ие приводится к следующему ряду: не может быть р.Фурье, т.к.его коэфф-ты не стремятся к нулю.