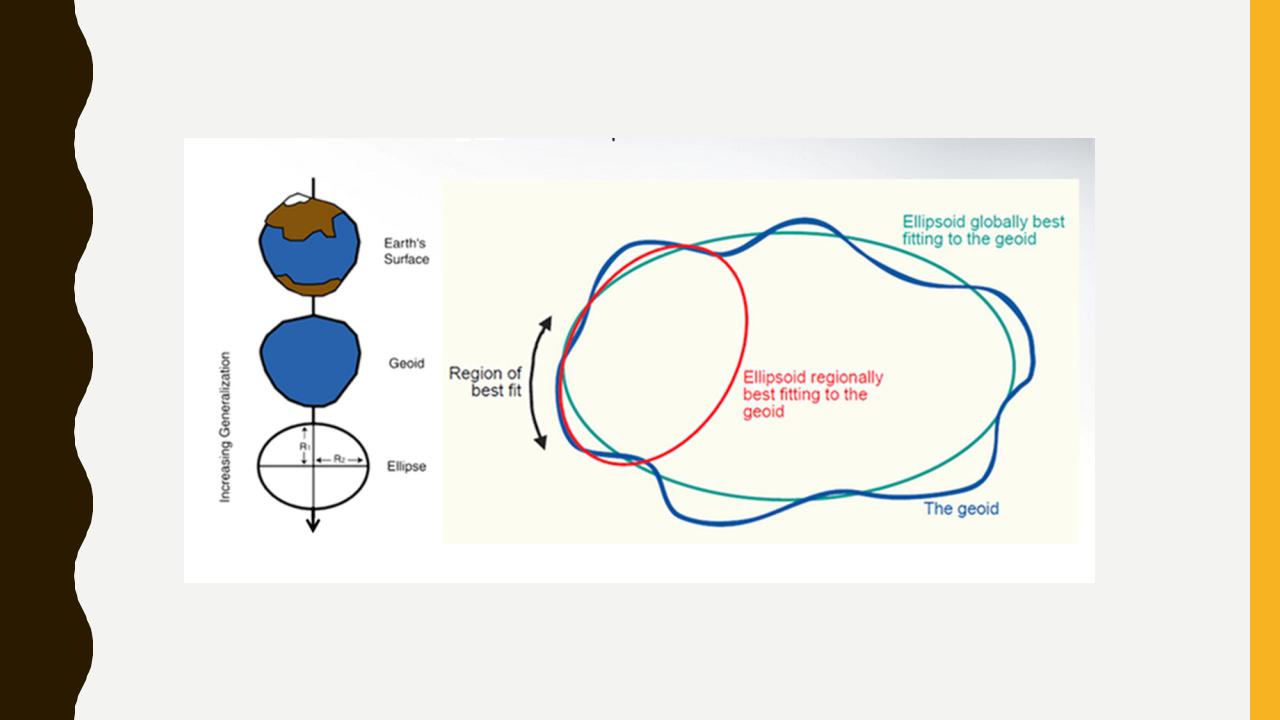
Земни́й еліпсо́їд— еліпсоїд обертання, який найкращим чином представляє фігуру геоїда.
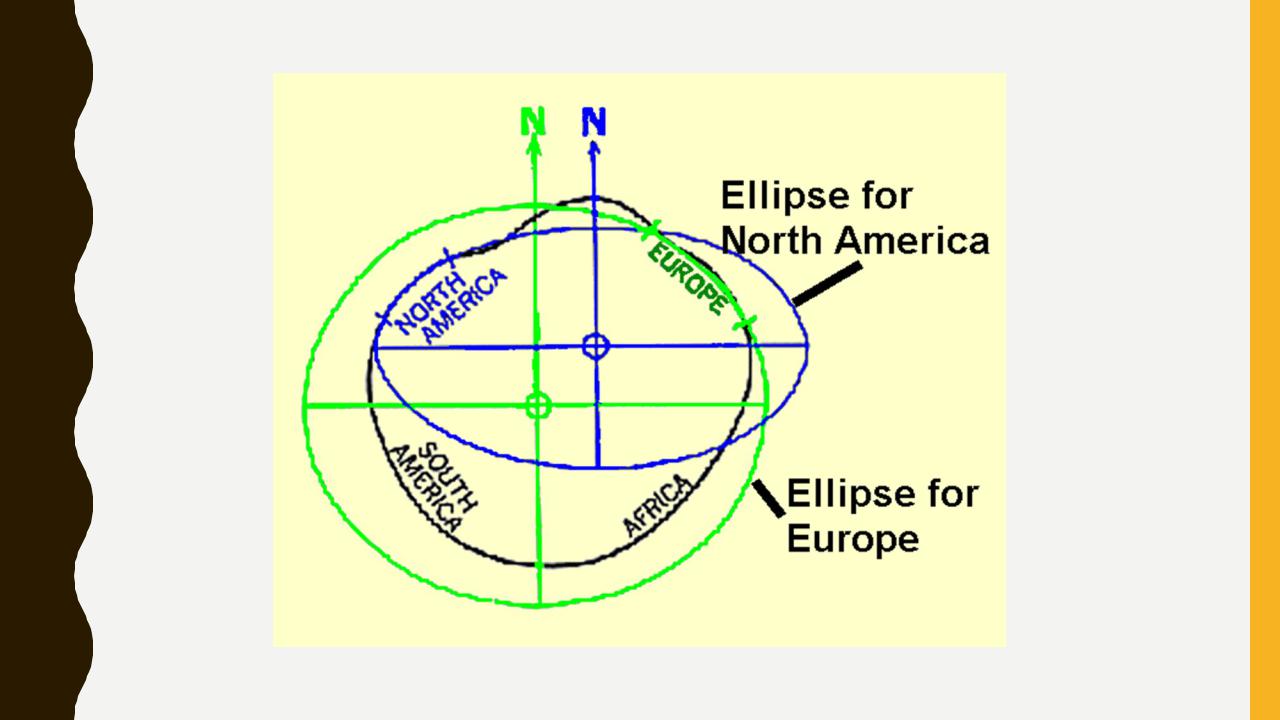
Еліпсоїд, що найбільш підходить до фігури Землі в цілому і центр якого збігається з центром мас Землі, називається загальним земним еліпсоїдом, а еліпсоїд, що найбільш близько підходить до поверхні геоїда на певній території (в межах держави, регіону чи континенту) і центр якого хоч і близько підходить, але не збігається з центром мас Землі називається референц-еліпсоїдом.
Референц-еліпсоїд — земний еліпсоїд обертання визначених розмірів і форми, орієнтований у тілі Землі, прийнятий для віднесення на нього
результатів усіх геодезичних і маркшейдерських вимірювань при обчисленні координат геодезичних та маркшейдерських пунктів.
Загальноземний еліпсоїд та референц-еліпсоїд
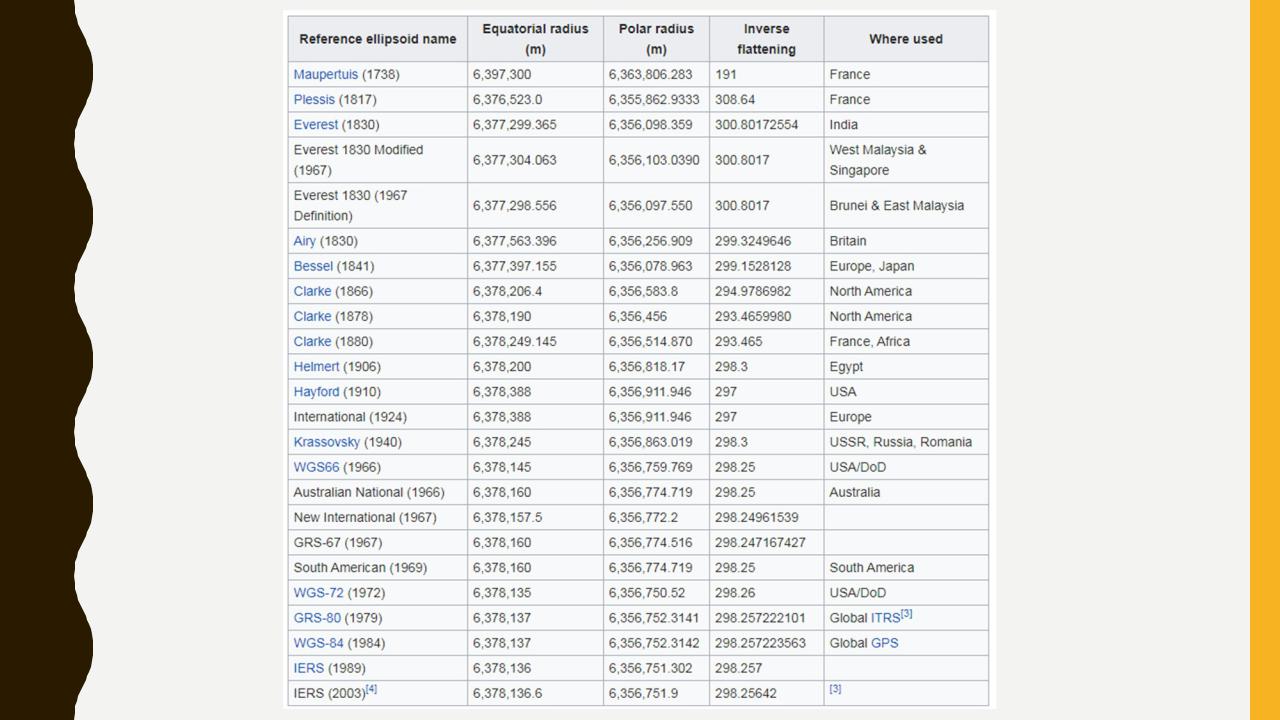
Параметри |
|
|
|
|
|
Формула |
|
|
|
|
|
|
|||||
Велика піввісь, а |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Стиснення, f |
|
|
|
|
|
f |
|
a b |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
Мала піввісь, b |
|
|
|
|
b a 1 |
|
f |
|
|
|
|
|
|
||||
Квадрат першого |
e2 a2 |
|
b2 |
|
e2 |
f 2 |
f |
|
|
||||||||
ексцентриситету |
|
|
|
|
|||||||||||||
меридіонального еліпса, e2 |
|
|
|
a2 |
|
|
|
|
|
|
|
|
|
|
|
||
Квадрат другого |
|
|
|
|
|
e 2 |
a2 |
b2 |
|
|
|
|
|
|
|||
ексцентриситету |
|
|
|
|
|
|
|
|
|
|
|
||||||
меридіонального еліпса e’2 |
|
|
|
|
|
|
|
|
b2 |
|
|
|
|
|
|
|
|
Радіус кривини меридіонального |
|
a 1 |
|
e2 |
|
|
|
|
|
|
|
|
|
|
|
||
M |
|
|
|
W |
|
1 e |
2 |
sin |
2 |
B , |
|||||||
еліпса М |
W |
3 |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
B – геодезична |
|||||||||||
Радіус кривини першого |
N |
|
a |
|
|
||||||||||||
|
|
|
широта |
|
|
|
|
||||||||||
вертикалу N |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
W |
|
|
|
|
|
|
|
|
|
|
|
|||||
СКІЛЬКИ НЕОБХІДНО ПАРАМЕТРІВ ЕЛІПСОЇДА ДЛЯ ОДНОЗНАЧНОГО ВИЗНАЧЕННЯ ?
• a, b |
2 |
• a, f |
параметри, |
• b, f |
один з |
• a, e2 |
яких |
• e2 ,f – немає розмірності |
повинен |
|
мати |
|
розмірніст |
СКІЛЬКИ НЕОБХІДНО ПАРАМЕТРІВ ЕЛІПСОЇДА ДЛЯ ОДНОЗНАЧНОГО ВИЗНАЧЕННЯ ?
•a, b
•a, f
•b, f
•a, e2
•e2 ,f – немає розмірності
Параметри референц-еліпсоїдів
Назва |
|
|
Велика піввісь |
|
|
Стиснення f |
|
|
еліпсоїда |
|
|
а, м |
|
|
|
||
|
|
|
|
|
|
|
||
GRS80 |
|
|
6378137.000 |
|
|
1/298.25722210 |
|
|
|
|
|
||||||
WGS84 |
|
|
6378137.000 |
|
|
1/298.25722356 |
|
|
Красовський |
|
|
6378245.000 |
|
|
1/298.30000000 |
|
|
Хейфорд |
|
|
6378388.000 |
|
|
1/297.00000000 |
|
|
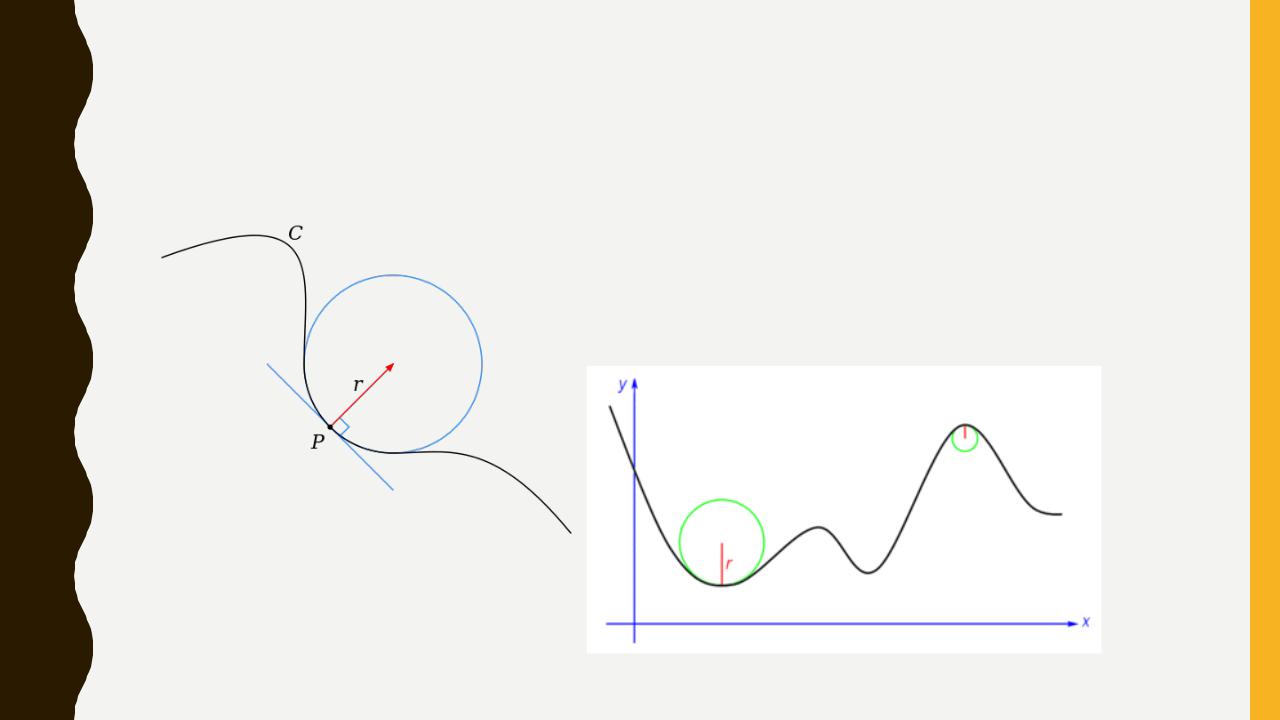
Радіус кривини рівний радіусу дотичного кола в заданій точці. Центр цього кола називається центром кривини.
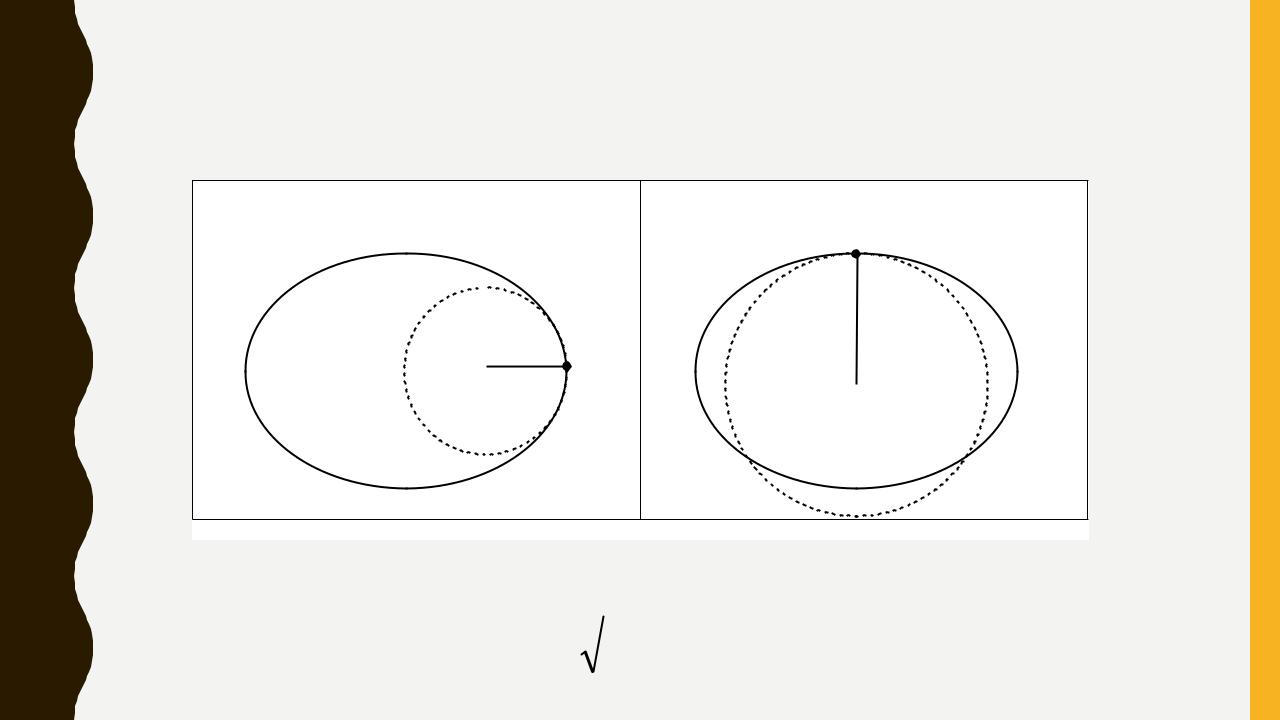
Нормальні (перпендикулярні) перерізи еліпсоїда, радіус кривини меридіонального еліпса М
Радіус кривини меридіонального |
Радіус кривини меридіонального |
еліпса на екваторі |
еліпса на полюсі |
M
M
M |
|
a 1 e2 |
|
|
|
3 |
|
(1 e2 sin 2 B) |
|||
