1 курс / 1 курс 2 семестр / Теория_вероятностей_17_22_лекц_1К

Теория вероятностей и математическая статистика

Лекция 17

1 курс. 4 зач.ед.

144 часа (36 час. лекц., 36 час. практич. зан., 72 час. самост. раб.). Экзамен.

1

Теория вероятностей и математическая статистика

Пример 1. По двум независимым выборкам объемов n1=12 и n2=15, извлеченным из нормальных генеральных совокупностей X и Y, найдены исправленные

уровне значимости 0,05 проверить нулевую гипотезу

Н0:D(Х)=D(Y) о равенстве генеральных дисперсий

при конкурирующей гипотезе Н1:D(Х) > D(Y).

Решение. Найдем отношение большей исправленной дисперсии к меньшей:

Fнабл = 11,41/6,52= 1.75.

Конкурирующая гипотеза имеет вид D(X) > D(Y), поэтому критическая область — правосторонняя.

2

Теория вероятностей и математическая статистика

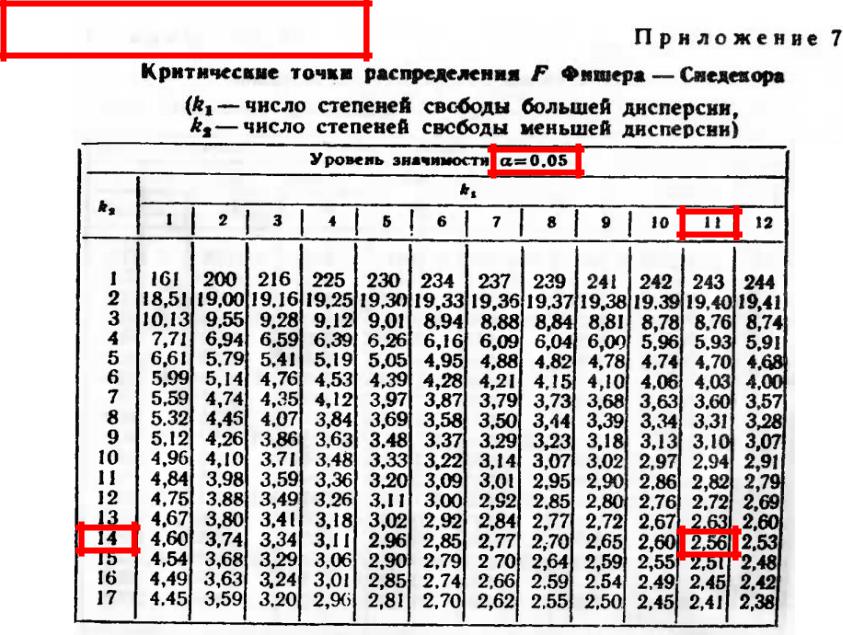
По таблице приложения 7, по уровню значимости = 0,05 и числам степеней свободы k1=12-1 = 11 и k2= 15-1 = 14 находим критическую точку Fкр(0,05; 11, 14).

3

Теория вероятностей и математическая статистика

Fкр(0,05; 11, 14) = 2,56.

4

Теория вероятностей и математическая статистика

Итак, для нашей задачи Fнабл = 1.75, а Fкр = 2.56.

Так как Fнабл < Fкр — нет оснований отвергать нулевую гипотезу о равенстве генеральных

дисперсий.

5

Теория вероятностей и математическая статистика

Второй случай.

Нулевая гипотеза H0: D (X) = D(Y). Конкурирующая гипотеза Н1: D(Х) D(Y).

В этом случае строят двустороннюю критическую область, исходя из требования, чтобы вероятность попадания критерия в эту область в предположении справедливости нулевой гипотезы была равна принятому уровню значимости .

6

Теория вероятностей и математическая статистика

Как выбрать границы критической области?

Можно показать, что наибольшая мощность

(вероятность попадания критерия в критическую область при справедливости конкурирующей гипотезы) достигается тогда, когда вероятность попадания критерия в каждый из двух интервалов критической области равна /2.

7

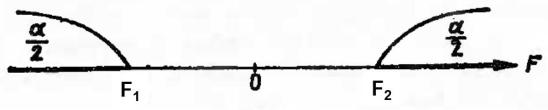
Теория вероятностей и математическая статистика

Таким образом, если обозначить через F1 левую границу критической области и через F2 — правую, то должны иметь место соотношения:

Р(F< F1) = /2, P(F> F2) = /2.

8

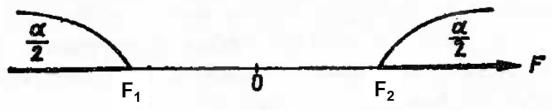
Теория вероятностей и математическая статистика

Мы видим, что достаточно найти критические точки, чтобы найти критическую область: F < F1 , F > F2, а также

область принятия нулевой гипотезы: F1 < F < F2.

Как практически отыскать критические точки?

9

Теория вероятностей и математическая статистика

Правую критическую точку F2 = Fкр( /2; k1, k2) находят непосредственно по таблице критических точек распределения Фишера—Снедекора по уровню значимости /2 и степеням свободы k1 и k2.

10