
Министерство науки и высшего образования Российской Федерации
Федеральное государственное бюджетное образовательное учреждение высшего образования
«ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ» (ТУСУР)
Кафедра комплексной информационной безопасности электронновычислительных систем (КИБЭВС)
ШИФРАТОРЫ И ДЕШИФРАТОРЫ
Отчет по лабораторной работе №2 по дисциплине «Электроника и схемотехника 2»
Вариант №18
Студент гр.
__.__.2022
Руководитель
__.__.2022
Томск 2022
Введение
Цель работы –научиться создавать шифраторы и дешифраторы на разных базисах и решать задачу увеличения их размерности.
Постановка задачи. Составить таблицы истинности для схем согласно варианту. Написать формулы для всех выходов в СДНФ или СКНФ. Собрать схемы согласно формулам, приведенным к базису согласно варианту. Так же требуется промоделировать каждую схему в двух режимах.
2
1.ШИФРАТОР 6-3
1.1ТАБЛИЦА ИСТИННОСТИ
Втаблице 1.1.1 приведена таблица истинности для шифратора 6-3(6 входов
и3 выхода).
Таблица 1.1.1 – таблица истинности шифратора 6-3
|
|
|
Входы |
|
|
|
|
Выходы |
|
||
E |
|
|
x |
|
|
|
|
a |
|
G |
|
|
5 |
4 |
3 |
|
2 |
1 |
0 |
2 |
1 |
0 |
|
0 |
x |
x |
x |
|
x |
x |
x |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
|
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
|
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
|
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
|
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
|
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1.2 ФОРМУЛА
Формула для выхода G в виде СДНФ:
= ∩ 5 ∩ 4 ∩ 3 ∩ 2 ∩ 1 ∩ 0 ∩ 5 ∩ 4 ∩ 3 ∩ 2 ∩ 1 ∩ 0
∩ 5 ∩ 4 ∩ 3 ∩ 2 ∩ 1 ∩ 0 ∩ 5 ∩ 4 ∩ 3 ∩ 2 ∩ 1 ∩ 0
∩ 5 ∩ 4 ∩ 3 ∩ 2 ∩ 1 ∩ 0 ∩ 5 ∩ 4 ∩ 3 ∩ 2 ∩ 1 ∩ 0
Формула для G в базисе И-НЕ:
= ( ∩ 5 ∩ 4 ∩ 3 ∩ 2 ∩ 1 ∩ 0) ∩ ( ∩ 5 ∩ 4 ∩ 3 ∩ 2 ∩ 1 ∩ 0)
∩( ∩ 5 ∩ 4 ∩ 3 ∩ 2 ∩ 1 ∩ 0) ∩ ( ∩ 5 ∩ 4 ∩ 3 ∩ 2 ∩ 1 ∩ 0) ∩
∩( ∩ 5 ∩ 4 ∩ 3 ∩ 2 ∩ 1 ∩ 0) ∩ ( ∩ 5 ∩ 4 ∩ 3 ∩ 2 ∩ 1 ∩ 0)
Формула для a0 в виде СДНФ:
0 = ∩ 5 ∩ 4 ∩ 3 ∩ 2 ∩ 1 ∩ 0 ∩ 5 ∩ 4 ∩ 3 ∩ 2 ∩ 1 ∩ 0
∩ 5 ∩ 4 ∩ 3 ∩ 2 ∩ 1 ∩ 0
Формула для a0 в базисе И-НЕ:
0 = ( ∩ 5 ∩ 4 ∩ 3 ∩ 2 ∩ 1 ∩ 0) ∩ ( ∩ 5 ∩ 4 ∩ 3 ∩ 2 ∩ 1 ∩ 0)
∩( ∩ 5 ∩ 4 ∩ 3 ∩ 2 ∩ 1 ∩ 0)
Формула для а1 в виде СДНФ:
1 = ∩ 5 ∩ 4 ∩ 3 ∩ 2 ∩ 1 ∩ 0 ∩ 5 ∩ 4 ∩ 3 ∩ 2 ∩ 1 ∩ 0
3
Формула для a1 в базисе И-НЕ:
1 = ( ∩ 5 ∩ 4 ∩ 3 ∩ 2 ∩ 1 ∩ 0) ∩ ( ∩ 5 ∩ 4 ∩ 3 ∩ 2 ∩ 1 ∩ 0)
Формула для а2 в виде СДНФ:
2 = ∩ 5 ∩ 4 ∩ 3 ∩ 2 ∩ 1 ∩ 0 ∩ 5 ∩ 4 ∩ 3 ∩ 2 ∩ 1 ∩ 0
Формула для а2 в базисе И-НЕ:
2 = ( ∩ 5 ∩ 4 ∩ 3 ∩ 2 ∩ 1 ∩ 0) ∩ ( ∩ 5 ∩ 4 ∩ 3 ∩ 2 ∩ 1 ∩ 0)
1.3 ФУНКЦИОНАЛЬНАЯ СХЕМА
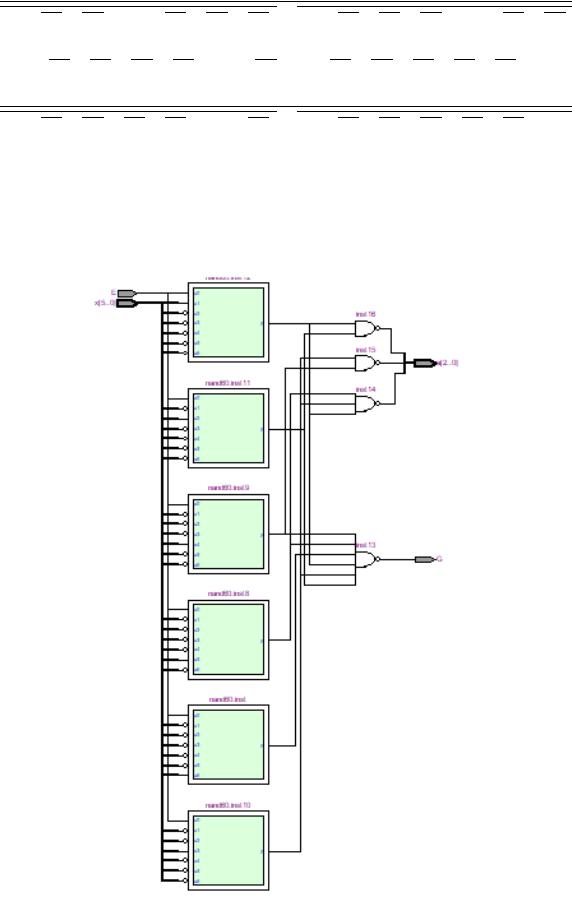
На рисунке 1.3.1 представлена функциональная схема.
Рисунок 1.3.1 – Функциональная схема
4
E, x[5..0] – являются входами, a[2..0], G – выходами, дающими результат схемы.
1.4 МОДЕЛИРОВАНИЕ
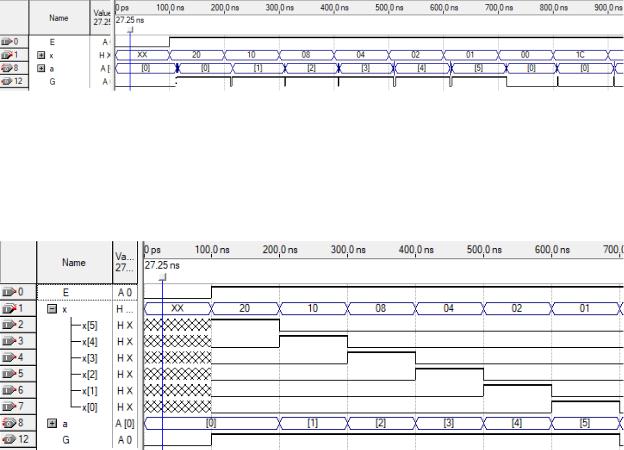
На рисунке 1.4.1 представлено моделирование схемы в режиме Timing.
Рисунок 1.4.1 – моделирование в режиме Timing
Так как моделирование в режиме Timing приближено к реальности и отображает задержки переключателя, из-за чего результат немного искажается от идеального. Сравнивания рисунок 1.4.1 и таблицу истинности 1.1.1, можно сделать вывод, что результаты совпадают.
На рисунке 1.4.2 представлено моделирование схемы в режиме Functional.
Рисунок 1.4.2 моделирование в режиме Functional
Один временной интервал равняется 100 наносекунд. Если сравнивать моделирование в режиме Functional, то оно полностью совпадает с таблицей иистинности.
1.5 КОД НА VHDL
Ниже представлен код схемы на VHDL: library ieee;
use ieee.std_logic_1164.all; entity Lab2_CD62 is
port (
x: in STD_LOGIC_VECTOR (5 downto 0); E: in STD_LOGIC;
G: out STD_LOGIC;
a: out STD_LOGIC_VECTOR (2 downto 0)); end;
5
architecture sync of Lab2_CD62 is
signal a_zn: STD_LOGIC_VECTOR (1 downto 0); begin
a<=a_zn; process(all) begin G<='1';
if E = '1' then case x is
when "100000" => a_zn <= "000"; when "010000" => a_zn <= "001"; when "001000" => a_zn <= "010"; when "000100" => a_zn <= "011"; when "000010" => a_zn <= "100"; when "000001" => a_zn <= "101"; G<='0';
end case; else
a_zn <= "000"; G<='0';
end if;
end process; end;
E, x[5..0] – является входами, G, a[2..0] – выходами, выдающими результат схемы.
1.6 СХЕМА ДЛЯ КОДА HDL
На рисунке 1.6.1 представлена схема для кода HDL в RTL viewer.
6
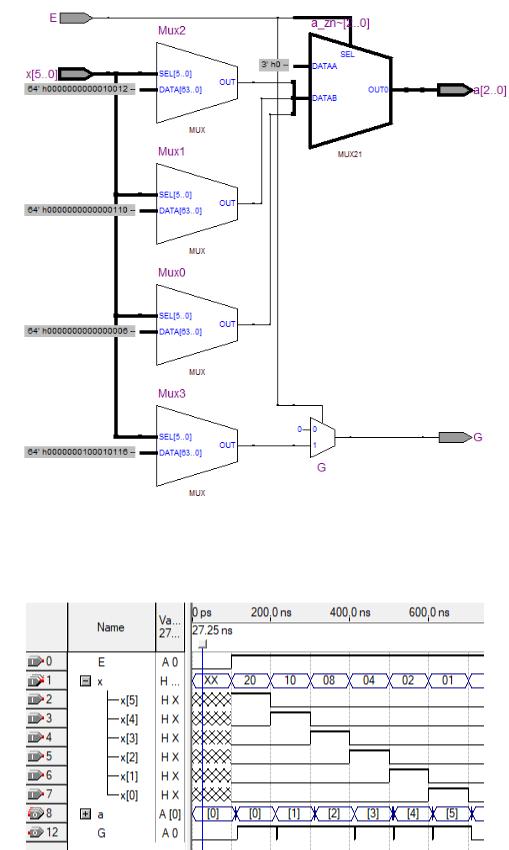
Рисунок 1.6.1 – схема из RTL viewer для кода HDL
1.7 МОДЕЛИРОВАНИЕ УСТРОЙСТВА, ОПИСАННОГО КОДОМ HDL
На рисунке 1.7.1 представлено моделирование кода в режиме Timing.
Рисунок 1.7.1 – моделирование схемы в режиме Timing
Из рисунка можно увидеть, что есть полная схожесть с таблицей истинности, а так же с моделированием по схеме.
7

2.ДЕШИФРАТОР 4-10
2.1ТАБЛИЦА ИСТИННОСТИ
Втаблице 2.1.1 приведена таблица истинности для шифратора 6-3(6 входов
и3 выхода).
Таблица 2.1.1 – таблица истинности шифратора 6-3
|
|
Входы |
|
|
|
|
|
|
Выходы |
|
|
|
|
||||
E |
|
|
a |
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
3 |
|
2 |
|
1 |
0 |
9 |
8 |
7 |
6 |
|
5 |
4 |
3 |
2 |
1 |
0 |
0 |
x |
|
x |
|
x |
x |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
|
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
|
0 |
|
0 |
1 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
|
0 |
|
1 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
|
0 |
|
1 |
1 |
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
|
1 |
|
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
|
1 |
|
0 |
1 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
|
1 |
|
1 |
0 |
0 |
0 |
0 |
1 |
|
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
|
1 |
|
1 |
1 |
0 |
0 |
1 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
|
0 |
|
0 |
0 |
0 |
1 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
|
0 |
|
0 |
1 |
1 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
2.2 ФОРМУЛА
Формулы в виде СДНФ:
0 = ∩ 0 ∩ 1 ∩ 2 ∩ 3 1 = ∩ 0 ∩ 1 ∩ 2 ∩ 3 2 = ∩ 0 ∩ 1 ∩ 2 ∩ 3 3 = ∩ 0 ∩ 1 ∩ 2 ∩ 3 4 = ∩ 0 ∩ 1 ∩ 2 ∩ 3 5 = ∩ 0 ∩ 1 ∩ 2 ∩ 3 6 = ∩ 0 ∩ 1 ∩ 2 ∩ 3 7 = ∩ 0 ∩ 1 ∩ 2 ∩ 3 8 = ∩ 0 ∩ 1 ∩ 2 ∩ 3 9 = ∩ 0 ∩ 1 ∩ 2 ∩ 3
Формулы в базисе ИЛИ-НЕ:
0 = 0 1 2 3
1 = 0 1 2 3
2 = 0 1 2 3
8
3 = 0 1 2 3 4 = 0 1 2 3 5 = 0 1 2 3 6 = 0 1 2 3 7 = 0 1 2 3 8 = 0 1 2 3 9 = 0 1 2 3
2.3 ФУНКЦИОНАЛЬНАЯ СХЕМА
На рисунке 2.3.1 представлена функциональная схема.
9
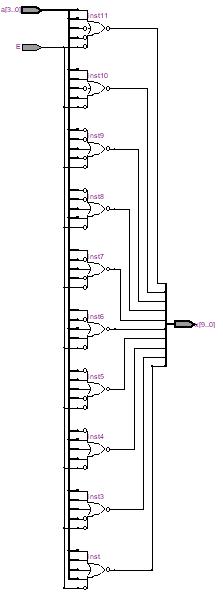
Рисунок 2.3.1 – Функциональная схема
E, a[3..0] – являются входами, x[9..0] – выходами, дающими результат схемы.
2.4 МОДЕЛИРОВАНИЕ
На рисунке 2.4.1 представлено моделирование схемы в режиме Timing.
10
