
Министерство науки и высшего образования Российской Федерации
Федеральное государственное бюджетное образовательное учреждение
высшего образования
«ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ
УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ» (ТУСУР)
Кафедра комплексной информационной безопасности электронно-
вычислительных систем (КИБЭВС)
ИЗУЧЕНИЕ РАБОТЫ СЧЕТЧИКОВ
Отчет по лабораторной работе №5 по дисциплине «Электроника и схемотехника 2»
Вариант №18
__.__.2022
Руководитель
_______
__.__.2022
Томск 2022
Введение
Цель работы – изучить двоичные счётчики, их принципы строения и работы.
Постановка задачи. Составить таблицы функционирования для заданных схем. Собрать схемы заданных счётчиков, делителя частоты и задержки.
Промоделировать все схемы, а также привести код на HDL и
промоделировать.
1.АСИНХРОННЫЙ СЧЕТЧИК
1.1ТАБЛИЦА ИСТИННОСТИ
Втаблице 1.1.1 приведена таблица функционирования асинхронного вычитающего счётчика на основе D триггера.
Таблица 1.1.1 – таблица функционирования
№ сигнала |
|
|
Выходы |
|
|
|
Q4 |
Q3 |
Q2 |
Q1 |
Q0 |
||
|
||||||
0 |
1 |
1 |
1 |
1 |
1 |
|
1 |
1 |
1 |
1 |
1 |
0 |
|
2 |
1 |
1 |
1 |
0 |
1 |
|
3 |
1 |
1 |
1 |
0 |
0 |
|
4 |
1 |
1 |
0 |
1 |
1 |
|
5 |
1 |
1 |
0 |
1 |
0 |
|
6 |
1 |
1 |
0 |
0 |
1 |
|
7 |
1 |
1 |
0 |
0 |
0 |
|
8 |
1 |
0 |
1 |
1 |
1 |
|
9 |
1 |
0 |
1 |
1 |
0 |
|
10 |
1 |
0 |
1 |
0 |
1 |
|
11 |
1 |
0 |
1 |
0 |
0 |
|
12 |
1 |
0 |
0 |
1 |
1 |
|
13 |
1 |
0 |
0 |
1 |
0 |
|
14 |
1 |
0 |
0 |
0 |
1 |
|
15 |
1 |
0 |
0 |
0 |
0 |
|
16 |
0 |
1 |
1 |
1 |
1 |
|
17 |
0 |
1 |
1 |
1 |
0 |
|
18 |
0 |
1 |
1 |
0 |
1 |
|
19 |
0 |
1 |
1 |
0 |
0 |
|
20 |
0 |
1 |
0 |
1 |
1 |
|
21 |
0 |
1 |
0 |
1 |
0 |
|
22 |
0 |
1 |
0 |
0 |
1 |
|
23 |
0 |
1 |
0 |
0 |
0 |
|
24 |
0 |
0 |
1 |
1 |
1 |
|
25 |
0 |
0 |
1 |
1 |
0 |
|
26 |
0 |
0 |
1 |
0 |
1 |
|
27 |
0 |
0 |
1 |
0 |
0 |
|
28 |
0 |
0 |
0 |
1 |
1 |
|
29 |
0 |
0 |
0 |
1 |
0 |
|
30 |
0 |
0 |
0 |
0 |
1 |
1.2 ФУНКЦИОНАЛЬНАЯ СХЕМА
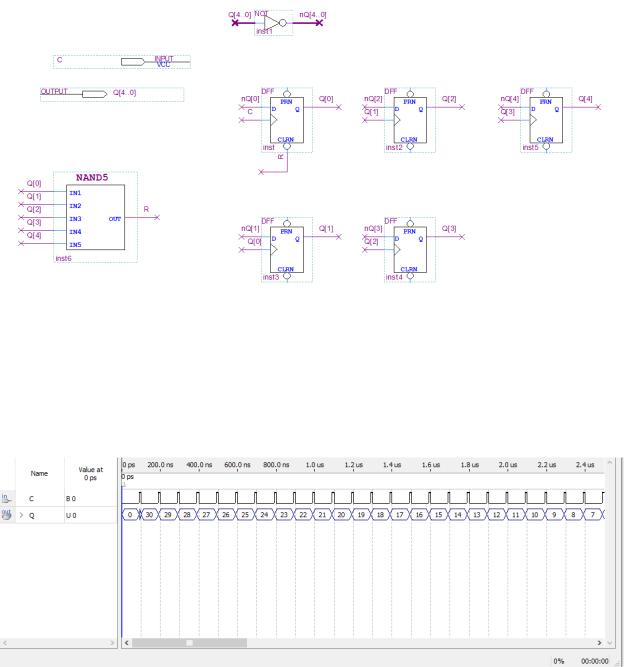
На рисунке 1.2.1 приведена функциональная схема для асинхронного счётчика на основе D триггера.
Рисунок 1.2.1 – функциональная схема
1.3 МОДЕЛИРОВАНИЕ
На рисунке 1.4.1 представлено моделирование в режиме Functional.
Рисунок 1.4.1 – моделирование схемы в режиме Funtional
Один временной интервал равен 100 наносекунд. Если сравнить моделирование с таблицей истинности, то они совпадают.
На рисунке 1.4.2 представлено моделирование в режиме Timing.
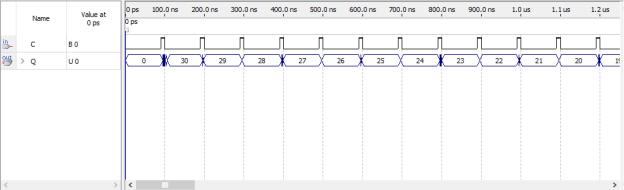
Рисунок 1.4.2 – моделирование в режиме Timing
Так как моделирование в режиме Timing приближено к реальности и
отображает задержки переключения, из-за чего результат немного искажается
от идеального.
1.4 КОД НА HDL
Ниже представлен код на SystemVeriLog HDL:
module chet_a_sv ( input C,
output [4:0] Q); logic R;
assign R = C | (~&Q);
always @ (posedge C, negedge R) begin if (~R) Q[0] <= 1'b0;
else Q[0] <= ~Q[0]; end
always @ (posedge Q[0]) begin Q[1] <= ~Q[1];
end
always @ (posedge Q[1]) begin Q[2] <= ~Q[2];
end
always @ (posedge Q[2]) begin Q[3] <= ~Q[3];
end
always @ (posedge Q[3]) begin Q[4] <= ~Q[4];
end endmodule

1.5 СХЕМА ИЗ RTL VIEWER ДЛЯ КОДА HDL
На рисунке 1.5.1 приведена схема из RTL Viewer для кода HDL.
Рисунок 1.5.1 – схема из RTL Viewer
1.6 МОДЕЛИРОВАНИЕ УСТРОЙСТВА, ОПИСАННОГО КОДОМ
HDL
На рисунке 1.6.1 представлено моделирование в режиме Timing для кода
HDL.
Рисунок 1.6.1 – моделирование устройства, описанного кодом HDL
2.СИНХРОННЫЙ СЧЕТЧИК
2.1ТАБЛИЦА ИСТИННОСТИ
Втаблице 2.1.1 приведена таблица функционирования синхронного суммирующего счётчика с асинхронным сбросом.
Таблица 1.1.1 – таблица функционирования
№ сигнала |
|
|
|
|
|
Выходы |
|
|
|
Q4 |
|
Q3 |
|
Q2 |
Q1 |
Q0 |
|
|
|
|
|
|||||
0 |
|
0 |
|
0 |
|
0 |
0 |
0 |
1 |
|
0 |
|
0 |
|
0 |
0 |
1 |
2 |
|
0 |
|
0 |
|
0 |
1 |
0 |
3 |
|
0 |
|
0 |
|
0 |
1 |
1 |
4 |
|
0 |
|
0 |
|
1 |
0 |
0 |
5 |
|
0 |
|
0 |
|
1 |
0 |
1 |
6 |
|
0 |
|
0 |
|
1 |
1 |
0 |
7 |
|
0 |
|
0 |
|
1 |
1 |
1 |
8 |
|
0 |
|
1 |
|
0 |
0 |
0 |
9 |
|
0 |
|
1 |
|
0 |
0 |
1 |
10 |
|
0 |
|
1 |
|
0 |
1 |
0 |
11 |
|
0 |
|
1 |
|
0 |
1 |
1 |
12 |
|
0 |
|
1 |
|
1 |
0 |
0 |
13 |
|
0 |
|
1 |
|
1 |
0 |
1 |
14 |
|
0 |
|
1 |
|
1 |
1 |
0 |
15 |
|
0 |
|
1 |
|
1 |
1 |
1 |
16 |
|
1 |
|
0 |
|
0 |
0 |
0 |
17 |
|
1 |
|
0 |
|
0 |
0 |
1 |
18 |
|
1 |
|
0 |
|
0 |
1 |
0 |
19 |
|
1 |
|
0 |
|
0 |
1 |
1 |
20 |
|
1 |
|
0 |
|
1 |
0 |
0 |
21 |
|
1 |
|
0 |
|
1 |
0 |
1 |
22 |
|
1 |
|
0 |
|
1 |
1 |
0 |
23 |
|
1 |
|
0 |
|
1 |
1 |
1 |
24 |
|
1 |
|
1 |
|
0 |
0 |
0 |
|
|
|
2.2 ФУНКЦИОНАЛЬНАЯ СХЕМА |
|
||||
На рисунке |
2.2.1 |
приведена |
функциональная |
схема для |
синхронного |
|||
суммирующего счетчика с асинхронным сбросом.

Рисунок 2.2.1 – функциональная схема
2.3 МОДЕЛИРОВАНИЕ
На рисунке 2.4.1 представлено моделирование в режиме Functional.
Рисунок 2.4.1 – моделирование схемы в режиме Funtional
Один временной интервал равен 100 наносекунд. Если сравнить моделирование с таблицей истинности, то они совпадают.
На рисунке 2.4.2 представлено моделирование в режиме Timing.
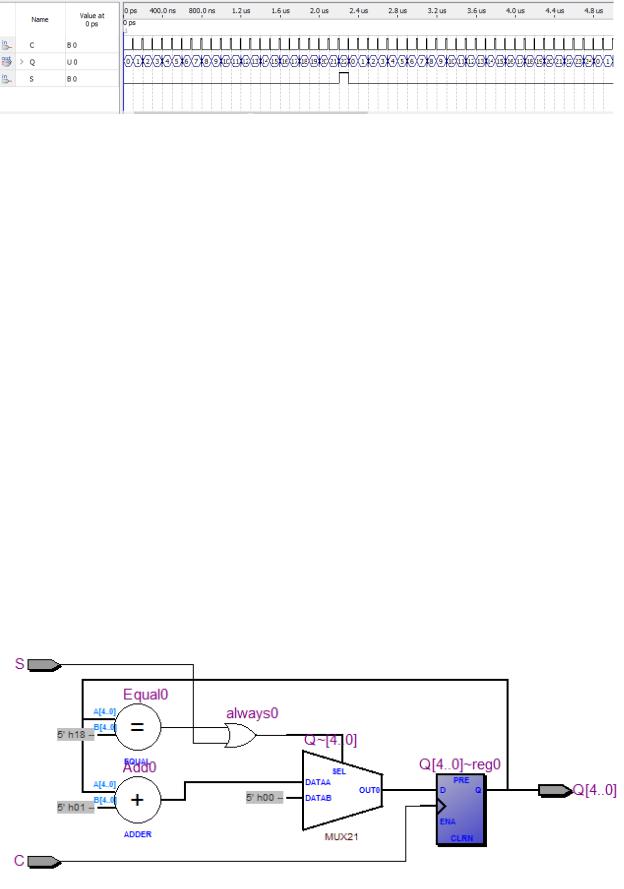
Рисунок 2.4.2 – моделирование в режиме Timing
Так как моделирование в режиме Timing приближено к реальности и
отображает задержки переключения, из-за чего результат немного искажается
от идеального.
2.4 КОД НА HDL
Ниже представлен код на SystemVeriLog HDL:
module chet_b_sv ( input C,
input S,
output [4:0] Q);
always_ff @ (posedge C) begin if (Q == 5'd24 | S) Q <= 5'd0; else Q <= Q + 1'b1;
end endmodule
2.5 СХЕМА ИЗ RTL VIEWER ДЛЯ КОДА HDL
На рисунке 2.5.1 приведена схема из RTL Viewer для кода HDL.
Рисунок 2.5.1 – схема из RTL Viewer

2.6 МОДЕЛИРОВАНИЕ УСТРОЙСТВА, ОПИСАННОГО КОДОМ
HDL
На рисунке 2.6.1 представлено моделирование в режиме Timing для кода
HDL.
Рисунок 2.6.1 – моделирование устройства, описанного кодом HDL
