5.2. Шифраторы и дешифраторы семейства ттл: функционирование и использование

Преобразователи унитарного позиционного кода в соответствующий двоичный код называют шифраторами (кодерами). Двоичные шифраторы – это комбинационные схемы, которые при подаче активного уровня на один из n информационных входов выдают на выходе слово позиционного двоичного кода, значение которого соответствует номеру активного входа. При этом разрядность выходного слова a составляет

a = int (log_2­n) разрядов, (18)

где int означает округление в бóльшую сторону до целого числа.

Запомните – количество выходов шифратора a ≤ n !

Ш

Рис. 16

ифратор с n входами иногда называют шифратором n х a (например, 10х4). Функциональное обозначение такого шифратора имеет вид, приведенный на рис. 16.

При подаче на входы одновременно нескольких активных сигналов большинство шифраторов реализует приоритет старшего номера, т.е. на выход выдается код сигнала с наибольшим номером входа. Поэтому на УГО шифраторы обозначают РRСD. Подробнее о разновидностях шифраторов см. /16/.

В шифраторах часто используются следующие дополни­тельные сигналы:

• входной сигнал включения шифратора — EI (Enable Input). Сигнал EI = 1 позволяет включить шифратор для приема информационных входных сигна­лов X_m, а сигнал EI = 0 – выключить. Сигнал обычно подается на инверсный вход;

• выходной сигнал, называемый групповым сигналом — GS (Group Signal), отмечающий (GS = 1) при включенном шифраторе (EI = 1) активное состояние хотя бы одного из входов (X_m = 1) шифратора и появление выходного кода Y_a-1...Y₁Y₀;

• выходной сигнал разрешения — ЕО (Enable Output), указывающий (EО = 1) при включенном шифраторе (ЕI = 1) на пассивное состояние всех входов шиф­ратора (X_m = 0 для m = 0, 1, 2, ..., n-1). Сигнал обычно выдается в инверсной форме.

Сигналы EI и ЕО предназначены для каскадирования приоритетных шифра­торов (поэтому ЕО обозначают также как EC – enable carry), сигнал GS — для запроса прерываний по вектору Y = {Y_a-1...Y₁Y₀} в микро­процессорных системах, так как выходные сигналы Y_a-1...Y₁Y₀ следует считы­вать только при активном уровне сигнала GS = 1.

К ак и другие преобразователи кодов, шифраторы могут быть аппаратно реализованы на логических элементах (SLC), на программируемой логике и на совокупности специальных микросхем.

Исходя из приведенного выше функционального описания простейший приоритетный шифратор без EI и ЕО имеет следующую таблицу функционирования (табл. 11).

В таблице вход Х1 имеет приоритет над входом Х0. Соответствующую принципиальную схему на логических элементах обучающимся следует изобразить самостоятельно.

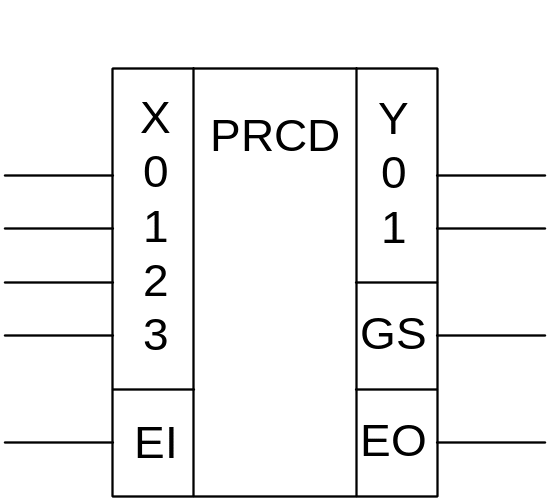
Построим схему приоритетного шифра­тора 4x2 с дополнительными входами и вы­ходами, УГО которого будет иметь вид, приведенный на рис. 17, а правила функционирования, исходя из описанной выше логики, приведены в табл. 12.

Т

Рис. 17

аблица 12

Входы					Выходы
EI	X3	X2	X1	X0	ЕО	GS	Y1	Y0
0	Ф	Ф	Ф	Ф	0	0	0	0
1	0	0	0	0	1	0	0	0
1	0	0	0	1	0	1	0	0
1	0	0	1	Ф	0	1	0	1
1	0	1	Ф	Ф	0	1	1	0
1	1	Ф	Ф	Ф	0	1	1	1

Составим структурные формулы:

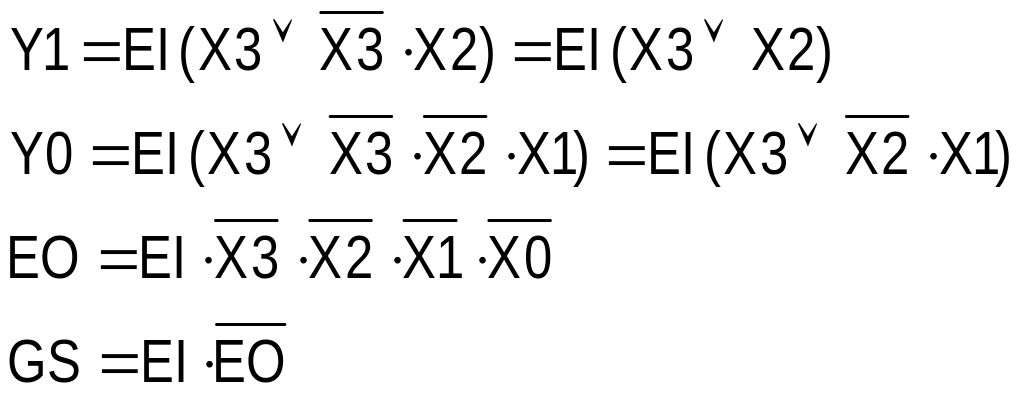
Принципиальная схема данного шифратора будет иметь вид, приведенный на рис. 18.

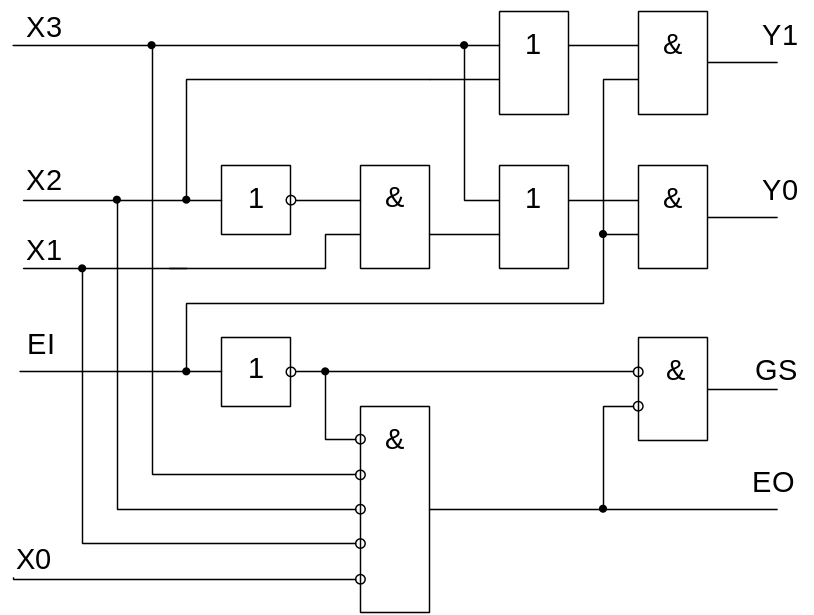
Рис. 18

В настоящее время в составе различных ТТЛ серий выпускается несколько законченных интегральных схем приоритетных шифраторов (ИВ1..ИВ3), УГО, схемы и функциональные возможности которых приведены в литературе /7-14/. Следует обратить внимание на то, что входы и выходы этих шифраторов инверсные. Микросхемы ИВ1, ИВ2 помимо основной функции – преобразования кода – выполняют индикацию наличия или отсутствия активных уровней хотя бы на одном из входов. Эти сигналы используются для разрешения работы смежных микросхем.

Для увеличения числа входов шифраторы соединяют как показано на рис. 19 для ИВ1 – РRСD 8х3. Здесь – разрешение включения, – сигнал наличия запроса (при =0 выдает лог.0 при наличии нуля хотя бы на одном входе), – сигнал отсутствия запросов, разрешающий работу «младших» шифраторов (т.е. реализующий межсхемный приоритет). и всегда имеют противоположные значения, кроме состояния запрета работы = 1, когда = = 1.

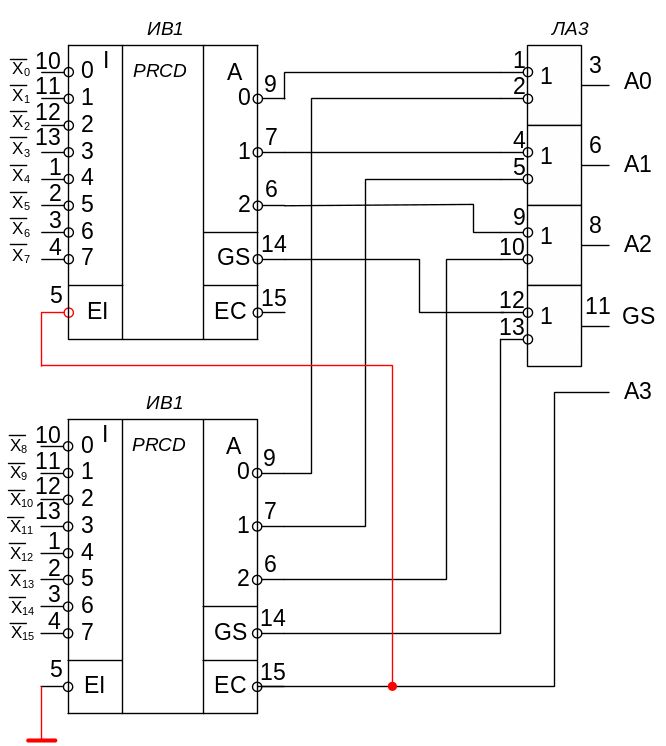
Рис. 19. Реализация межсхемного приоритета

Если использовать К555ИВ2, имеющий выходы с Z-состоянием (рис. 20, а), то наращивание разрядности можно делать монтажно, без микросхем НЕ-ИЛИ. Особенно важно это, когда шифраторов много (например, 64х6 разрядов, где нужны 8-входовые схемы – изобразите эту схему самостоятельно).

В семействе ТТЛ выпускается также ИВ3 – РRСD 10х4 (рис. 20, б) с девятью входами без логики расширения. Эта микросхема предназначена для преобразования унитарного кода в – какой?

Используются приоритетные шифраторы для построения контроллеров клавиатуры, интерфейсов ввода сигналов путевых датчиков и т.п.

Для удобства сопряжения с клавиатурами и т.п. периферийными устройствами схему шифраторов обычно организуют так, чтобы активным уровнем на входах и выходах служил лог.0.

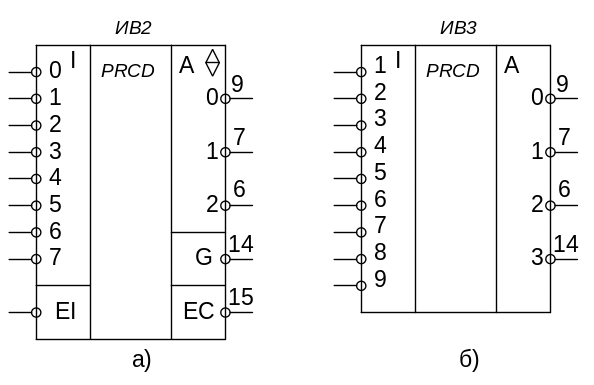
Рис. 20

Обратная процедура – преобразование двоичного кода в соответствующий унитарный позиционный код (обычно с инверсией) – выполняется дешифраторами. Таким образом, двоичные дешифраторы – это комбинационные схемы, которые при подаче на входы a-разрядного слова позиционного двоичного кода выдают активное состояние на том (единственном) из n выходов, номер которого соответствует значению поданного на входы кода (рис. 21). П

Рис. 21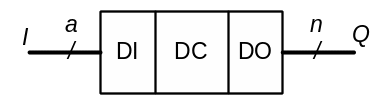

ри этом коли­че­ст­во выходов составляет n ≤ 2_­^a разрядов.

Запомните – количество выходов дешифратора  n > a!

На УГО дешифраторы обозначают DC. Следует обратить внимание на то, что выходы дешифраторов обычно инверсные, соответственно на невыбранных выходах (если нет третьего состояния) сохраняется потенциал лог.1.

Д

Рис. 22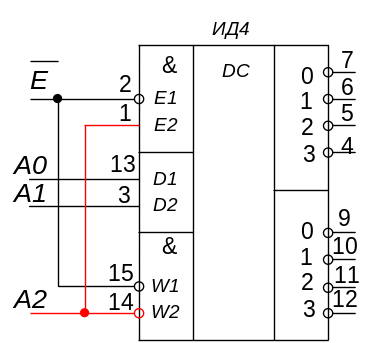

ля управления (например, для расширения разрядности) дешифраторы имеют входы разрешения. Так, дешифратор ИД4, который особо популярен в УЧПУ ввиду своих широких возможностей, соответственно может использоваться и как сдвоенный дешифратор двухразрядного кода на 4 выхода и как дешифратор трехразрядного кода на 8 выходов (рис. 22). Обратите внимание: входы Е1, W1, W2 инверсные, Е2 – прямой. Составьте таблицу функционирования этого дешифратора со столбцами А2-А1-А0-Port-Pin.

В семейство ТТЛ входят дешифраторы 155ИД3 (16 вы­ходов), 155ИД7 (8 выходов), ИД12 (8 выходов с открытым эмиттером и токозадающими резисторами). Дешифраторы могут быть и сдвоенными, например ИД14 (2х4 выхода). УГО популярных дешифраторов имеют вид, приведенный на рис. 23. Постройте на основе ИД7 дешифраторы на 20 выходов и на 60 выходов.

Дешифраторы выпускают полные и неполные. Неполные дешифраторы используются, например, для получения сигналов, соответствующих десятичной цифре (n=10) или для опознавания адреса устройства (n=1 – минимальное значение).

Существуют схемы без входов управления. Это обычно неполные дешифраторы, например ИД6 (4х10), ИД10 (4х10 с ОК – см. рис. 23). Они, как правило, рассчитаны на непосредственную (без дополнительного умощнения) работу с различными индикаторами, имеющими 10 символов. Например, К155ИД1 (4х10, выходы с ОК рассчитаны на 60 В) предназначен для управления газоразрядными индикаторами.

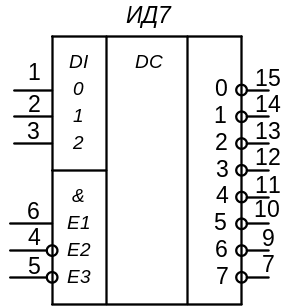
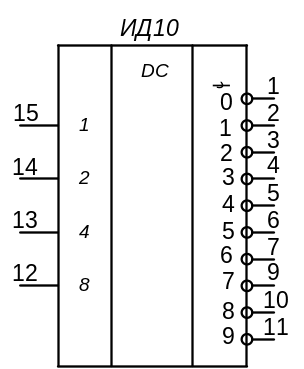
Рис. 23

Дешифраторы совместно со схемами ИЛИ можно использовать для воспро­изведения произвольных логических функций. Действительно, на выходах дешифратора вырабатываются все конъюнктивные термы (конституенты единицы), которые только можно составить из данного числа аргументов. Логическая функция в СНДФ есть дизъюнкция некоторого числа таких термов. Собирая нужные термы по схеме ИЛИ, можно получить любую функцию данного числа аргументов. Такое решение может быть целесообраз­ным при необходимости выработки нескольких функций одних и тех же аргументов. В этом случае для выработки дополнительной функции добав­ляется только один дизъюнктор. Заметим, что для синтеза схемы удобно перевести заданные функции в СДНФ.