6. Электрическое моделирование колебаний механических систем. Масштабные коэффициенты. Индикаторы подобия

Для того, чтобы при моделировании аналогичные явления были подобными, соотношения между моделируемыми и моделирующими величинами должны удовлетворять соответствующим условиям. Для установления этих условий вернемся к системам электромеханической аналогии Максвелла (см. рис. 7) и сравним их уравнения движения (1) и (3).

( ) ( , , )

Рис. 7. Электромеханическая аналогия Максвелла

. (16)

. (17)

Введем следующие отношения:

, , , , .

Так как скорости моделируемого и моделирующего процессов различны, то положим, что отношение времени моделируемого и времени моделирующего процессов равно числу .

Числа называют масштабными коэффициентами. Все они, кроме , имеют размерность.

Выразим механические величины через электрические с помощью масштабных коэффициентов:

, , , , , ,

, .

Подставив эти величины в уравнение (16) и преобразовав его, получим:

. (18)

Чтобы моделируемое и моделирующее явления были аналогичны, необходимо, чтобы уравнения (16) и (18) были идентичны, т.е. должны выполняться условия:

, , . (19)

Соотношения (19) называют индикаторами или критериями подобия. Шесть чисел связаны тремя соотношениями (19), следовательно только три масштабных коэффициента являются независимыми. Например, если – независимы, то для остальных чисел получаем соотношения:

, , . (20)

Если число степеней свободы системы больше 1, соотношения (19) сохраняются, так как сложные системы можно рассматривать как состоящие и нескольких простых, которые подобны как в отдельности, так и в целом, если соблюдено подобие сопряжения простых систем и граничные условия.

Пример 4. Осуществить подбор масштабных коэффициентов для механической системы, электрическая модель которой представлена на рис. 8. Дано: , , , , , , , , , (1 ).

Рис. 8. Механическая система и ее электрическая модель

Найдем

.

С другой стороны

.

Отсюда определяем

.

Аналогично находим

.

Поскольку

,

Вычисляем

.

Вычисляем

.

Определяем

.

Таким образом, в моделирующей электрической системе явления протекают в 500 раз быстрее, чем в механической.

Учитывая, что

,

находим

,

Вычисляем коэффициент

.

Некоторые радиотехнические электрические системы и их механические аналоги приведены в приложении.

7. Составление уравнений лагранжа для исследования неголономных систем

Рассмотрим динамическую систему, на движение которой наложена кинематическая связь. При этом вектор скорости одной из точек тела системы сохраняет свое направление по отношению к этому движущемуся телу. Для механической системы эта связь типична в случае, когда твердое тело, двигающееся по поверхности, имеет острие, врезающееся в неподвижную поверхность – вектор скорости точки острия сохраняет свое направление относительно тела. Для электромеханической системы кинематическую связь можно представить как проводник с током, положение которого не меняется относительно подвижной части системы (ротора). В этих случаях кинематическая связь, накладываемая на скорости (токи), является неинтегрируемой. Уравнения Лагранжа (4), записанные в голономных координатах, для исследования подобных систем неприменимы. Необходимо вводить новые неголономные координаты и использовать уравнения движения в этих координатах. Такие уравнения можно представить в виде (форма Лагранжа-Эйлера):

, (21)

где индекс пробегает по всем независимым неголономным координатам, – независимые неголономные координаты, вводящиеся преобразованием:

, (22)

где – число старых голономных координат.

Направляющие косинусы преобразованных координат и кинетическая энергия системы, выраженная в неголономных координатах, вычисляются по формулам:

,

Величина кинетической энергии может быть также записана в виде:

,

Где – метрический тензор неголономных координат, – метрический тензор исходной системы голономных координат. Он определяется метрикой пространства:

.

Величина определяется через направляющие косинусы преобразования координат:

.

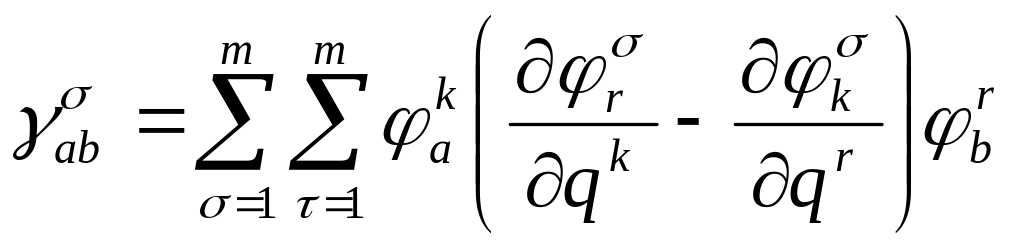Введение новых координат диктуется удобством решения задачи. Неголономность координат зависит от интегрируемости соотношения (22). Оно состоит в выполнении равенства:

. (23)

Если условие (23) не выполняется, то новые координаты являются неголономными

Пример 5. Осуществить переход от осей, жестко связанных с ротором электродвигателя, к стационарным неподвижным осям. На рис. 9 изображены оси и , жестко связанные с ротором, вращающимся со скоростью , и – стационарные неподвижные оси, – угол, определяющий взаимное расположение неподвижных и вращающихся осей в момент времени, когда ротор совершил оборотов. Ось совпадает с осью вала ротора. – орты соответствующих осей координат.

Рис. 9. Переход от осей, жестко связанных с ротором электродвигателя, к стационарным неподвижным осям

Выберем обобщенные координаты в системе координат, связанных с ротором: , (количества электричества в проводниках вдоль осей и ), (угол поворота ротора). Обобщенные скорости и токи:

, , .

При переходе к стационарным осям преобразуются не сами обобщенные координаты, а их производные. В соответствии с рис. 9 получаем:

,

, (24)

Здесь , , – обобщенные скорости и токи в новых осях координат. Направляющие косинусы преобразования при этом имеют вид:

.

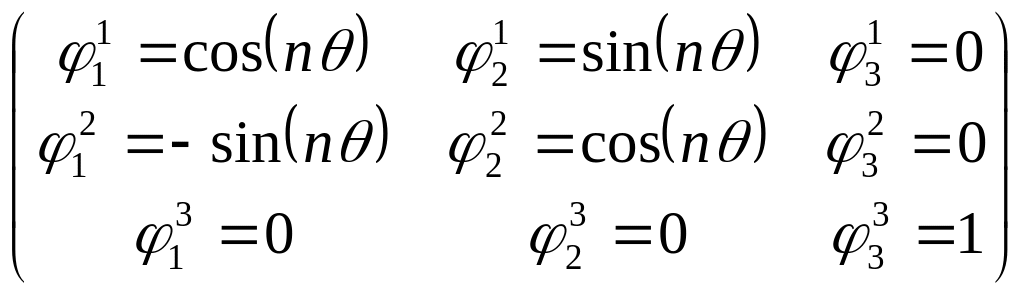Преобразование токов играет роль кинематической связи. Проверим условии (23) неголономности новых координат. Применив дифференцирование, получаем:

,

,

.

Неравенство этих производных показывает, что новые координаты являются неголономными. Для описания электромеханизма в стационарных координатах необходимо пользоваться уравнениями движения (21) в неголономных координатах.