4. Составление уравнений лагранжа для электрических цепей с сосредоточенными параметрами
Если использовать методику составления уравнений Лагранжа второго рода, но вместо обычных механических величин брать электрические (см. табл.), то уравнения (2.1) будут являться уравнениями многоконтурной электрической системы. Рассмотрим несколько примеров электромеханических аналогий
Пример 1. Применить методику составления уравнений Лагранжа второго рода для электрического контура с двумя степенями свободы, изображенного на рис. 2.
1.
Определим число степеней свободы
электрической цепи.
Каждая электрическая цепь состоит из ветвей и узлов. Совокупность ветвей и узлов, по которым возможен замкнутый обход, называется контуром. Токи, протекающие по ветвям, связаны законами Кирхгофа:
для каждого узла
, (7)
для каждого контура
. (8)
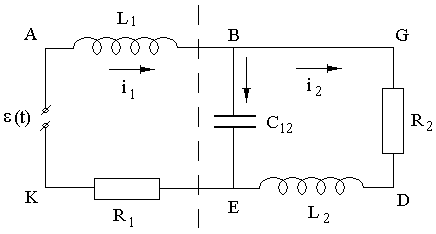
Рис. 2. Электрический контур с двумя
степенями свободы
Пусть
цепь содержит
ветвей и
узлов. По ветвям протекают количества
электричества
с силами токов
,
.
Соотношения (7) надо рассматривать как
уравнения связи для
.
Для
узлов число таких независимых уравнений
будет равно
.
Если
в рассматриваемой цепи содержится
источник ЭДС, то ток в этой ветви
определяется данным источником. Если
вся цепь содержит
источников, то число степеней свободы
электрической цепи вычисляется по
формуле:
. (9)
Для многосвязных электрических контуров эта формула дает
, (10)
где
– число односвязных контуров,
,
,
– суммы соответствующих величин для
многосвязного электрического контура.
Для
рассматриваемого примера (рис. 2) задание
силы тока
на участке
и
на участке
полностью определяет силу тока на любом
участке. Следовательно, число степеней
свободы данной электрической системы
.
2.
Составим выражения для
,
,
как суммы соответствующих величин во
всей цепи:
,
,
.
3. Вычислим обобщенные силы.
Вынуждающая
обобщенная сила по первой координате
определяется из условия
по выражению для элементарной работы
электрических сил с учетом (5):
.
Отсюда
Потенциальная
обобщенная сила
,
соответствующая первой обобщенной
координате
,
равна
.
Диссипативная
обобщенная сила
,
соответствующая первой обобщенной
координате
,
равна
.
Производные, входящие в уравнение Лагранжа второго рода для первой степени свободы, равны
,
.
Добавочная
обобщенная сила по второй координате
определяется из условия
,
тока
на участке
нет, источник ЭДС на
отключен, на
других источников нет и
.
Далее вычисляем:
,
,
,
.
После подстановки в (4) получаем искомую систему двух уравнений:
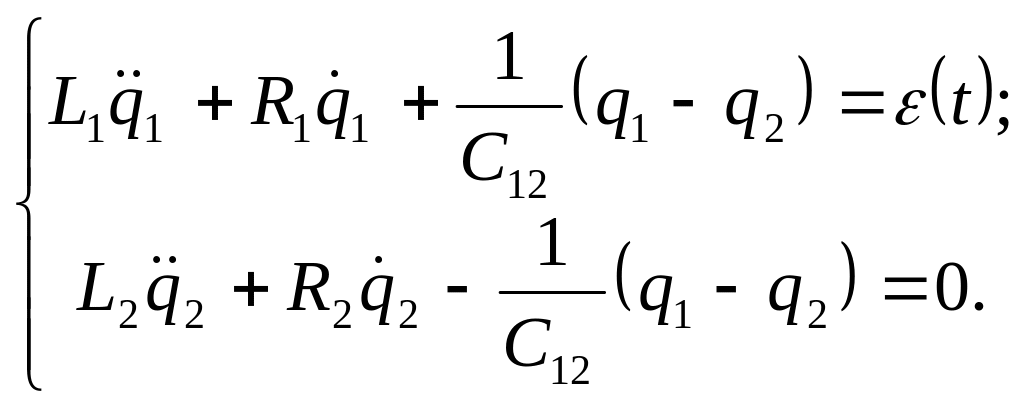
Как видно из полученной системы, уравнения Лагранжа для электрической цепи выражают действительный баланс электродвижущих сил в -контурной цепи (второй закон Кирхгофа).
Пример 2. Составить контурные уравнения для электрической цепи, изображенной на рис. 3, используя аналогию Максвелла, и установить ее механической аналог.
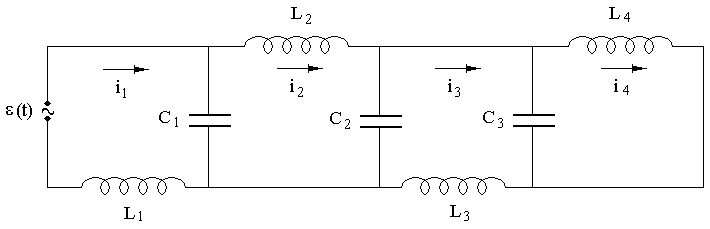
Рис. 3. Электрический контур с четырьмя
степенями свободы
Как и в предыдущем примере определим число степеней свободы электрической цепи, составим выражения для , , , вычислим обобщенные силы и запишем систему уравнений.
.
– обобщенные
координаты.
Уравнения Лагранжа в этом случае имеют вид:
,
.
(Диссипативная функция равна нулю, т.к. в системе не содержатся сопротивления).
Вычисляем:
,
,
,
,
,
.
Окончательно получаем систему четырех уравнений:
.
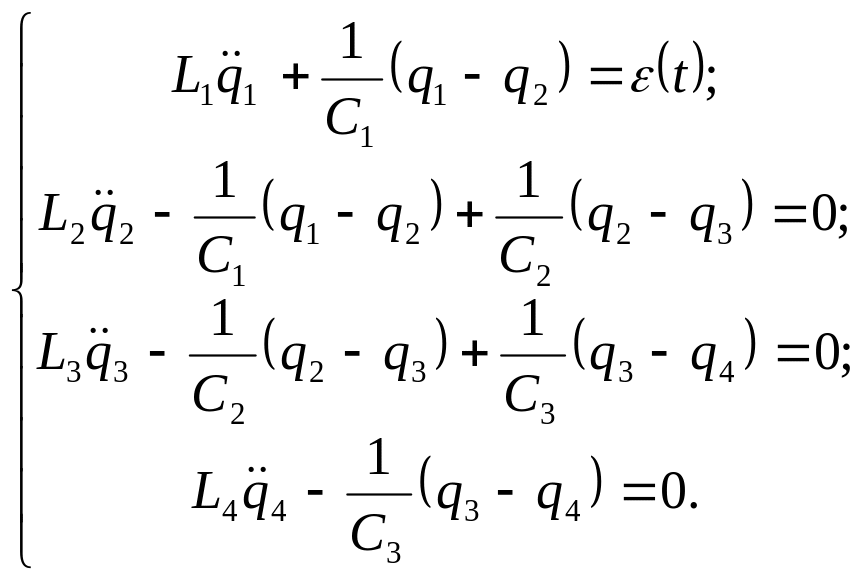Эти уравнения аналогичны дифференциальным уравнениям вынужденных колебаний без учета сил сопротивления механической системы, изображенной на рис. 4.
Рис. 4. Механическая система с четырьмя
степенями свободы
Дифференциальные уравнения движения данной механической системы будут иметь вид:
.
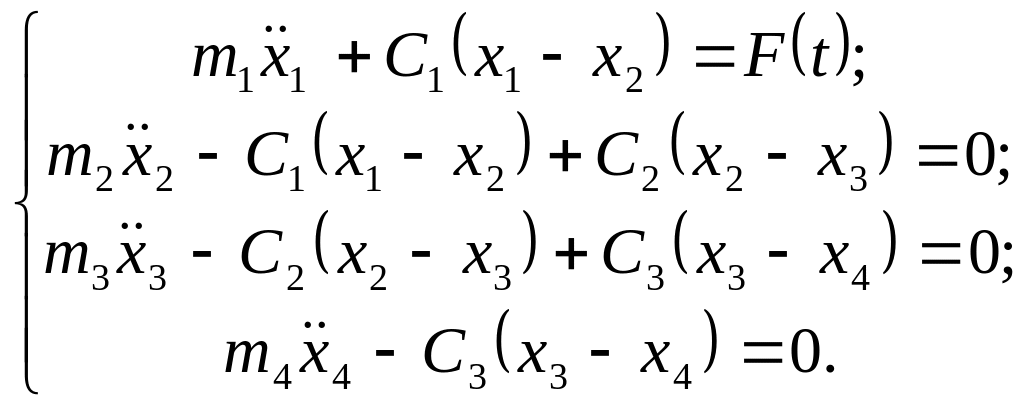Очевидно, что каждое уравнение данной системы вытекает из второго закона Ньютона, записанного для каждого из четырех движущихся тел. Система, изображенная на рис. 4, является механическим аналогом электрической системы, приведенной на рис. 4.