2. Электромеханическая аналогия максвелла

Проведем сравнительный анализ двух простейших колебательных систем – механической и электрической (рис. 1). Тело движется поступательно вдоль оси под действием переменной силы , зависящей от времени, силы упругости , пропорциональной смещению тела, и силы сопротивления , пропорциональной скорости тела. Начало координат соответствует недеформированной пружине в начальный момент времени.

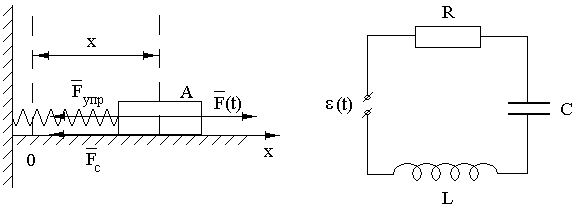
Рис. 1. Первая электромеханическая аналогия

(аналогия Максвелла): механическая и электрическая

системы с одной степенью свободы

Уравнение движения тела имеет вид:

. (1)

Кинетическая и потенциальная энергии и функция рассеяния Релея, соответственно:

, , . (2)

Замкнутый колебательный контур представляет собой линейную электрическую цепь с сосредоточенными параметрами – сопротивлением , конденсатором , катушкой индуктивности и источником ЭДС . Обозначим заряд на конденсаторе , силу тока в цепи и запишем в данный момент времени известные соотношения для падения напряжения на сопротивлении, конденсаторе и катушке , и , соответственно:

, , .

Т.к. , то

. (3)

Сопоставление уравнений (1) и (3) показывает, что если обеспечить пропорциональность между коэффициентами, то решения этих уравнений при соответствующем подборе начальных данных будут отличаться лишь постоянным множителем. Физические системы считаются аналогичными, если они описываются одинаковыми дифференциальными уравнениями. Соответствие решений уравнений (1) и (3) позволяет экспериментально исследовать механическую систему с помощью измерений на электрической и наоборот.

Сведем аналогичные величины в таблицу 2.

3. Уравнения лагранжа второго рода

Пусть на систему, имеющую степеней свободы, наложены голономные связи и действуют потенциальные, диссипативные и вынуждающие связи. Уравнения ее движения в обобщенных координатах имеют вид:

, . (4)

Здесь – обобщенная координата, – обобщенная сила, отнесенная к обобщенной координате , – кинетическая энергия системы. Эти уравнения образуют систему уравнений Лагранжа второго рода. Число уравнений Лагранжа равно числу независимых обобщенных координат, т.е. числу степеней свободы системы.

Таблица 2 Система электромеханических

аналогий Максвелла

Механическая система	Электрическая система
Смещение	Заряд
Скорость	Сила тока
Масса	Индуктивность
Коэффициент вязкого сопротивления	Омическое сопротивление
Жесткость пружины	Обратная емкость
Обобщенная сила	ЭДС
Кинетическая энергия	Энергия магнитного поля катушки
Потенциальная энергия	Энергия поля конденсатора
Диссипативная функция	Диссипативная функция

Уравнения Лагранжа для обобщенных координат являются обыкновенными дифференциальными уравнениями второго порядка, как и дифференциальные уравнения движения точки в декартовых координатах.

Обобщенная сила в общем случае вычисляется как коэффициент при приращении обобщенной координаты в выражении элементарной работы действующих на систему сил:

. (5)

Обобщенные потенциальная и диссипативная силы вычисляются по формулам:

, . (6)