5. Электромеханические системы и примеры применения уравнений лагранжа для исследования колебаний этих систем

Колебательные процессы, как в механических, так и в электрических системах представляют собой явления, заключающиеся в преобразовании с течением времени одних форм энергии в другие.

Т.к. механическая и электромагнитная энергии взаимно обратимы, то механические и электрические системы могут быть объединены на основе преобразования энергии в соответствии с первым началом термодинамики (обобщенным законом сохранения энергии). При этом между механическими и электрическими переменными системы устанавливаются зависимости, определяемые уравнениями связи.

Уравнения Лагранжа имеют энергетическую основу, поэтому позволяют установить эти зависимости.

Электромеханические системы – это такие совокупности электрических и механических цепей, в которых механические и электрические процессы протекают взаимно обусловлено. Поэтому среди обобщенных координат системы должны быть параметры, характеризующие и электрические явления ( – количество электричества, протекающего по разным ветвям), и геометрические координаты.

Общее число независимых обобщенных координат равно общему числу степеней свободы системы:

, (11)

где – число электрических степеней свободы, т.е. число независимых количеств электричества, протекающих по разным ветвям, – число механических степеней свободы, т.е. число фиксируемых параметров, при которых система не совершает перемещений.

Аналогично должны быть представлены кинетическая и потенциальная энергии, функция рассеяния и обобщенные силы электромеханической системы:

, , , . (12)

Рассмотрим выражения для через параметры электрической цепи с степенями свободы. Связи полагаются идеальными, стационарными, голономными.

Энергия магнитного поля витка с током и постоянной индуктивностью равна . Добавочная энергия магнитного поля двух индуктивно связанных витков с токами и равна , где – коэффициент взаимной индукции. Полная кинетическая энергия системы двух витков равна

.

Если в контуре с током магнитный поток сцепления порожден не током другого контура, а постоянным магнитом, то добавочная энергия магнитного поля равна .

Таким образом, для цепи из ветвей, из которых связаны взаимной индукцией, а сцеплены с постоянными магнитами, электрокинетическая энергия вычисляется по формуле:

. (13)

Так как уравнения связей для токов линейны (законы Кирхгофа), то – квадратичная функция своих аргументов.

Коэффициенты и в вакууме постоянны, а в магнитной среде зависят от токов.

При наличии конденсаторов емкостью , электрическая система обладает потенциальной энергией, являющейся квадратичной функцией независимых количеств движения :

. (14)

Если электрическая система содержит омических сопротивлений, то электрическая диссипативная функция является квадратичной функцией независимых токов

. (15)

Пример 3. Конденсаторный микрофон (рис. 5) состоит из последовательно соединенных катушки самоиндукции с индуктивностью , омического сопротивления и конденсатора, пластины которого связаны двумя пружинами общей жесткости . Цепь подсоединена к элементу постоянной ЭДС , на пластину конденсатора действует переменная сила . Емкость конденсатора в положении равновесия , расстояние между пластинами при этом . Масса подвижной пластины конденсатора (диафрагмы) . Составить дифференциальные уравнения движения системы.

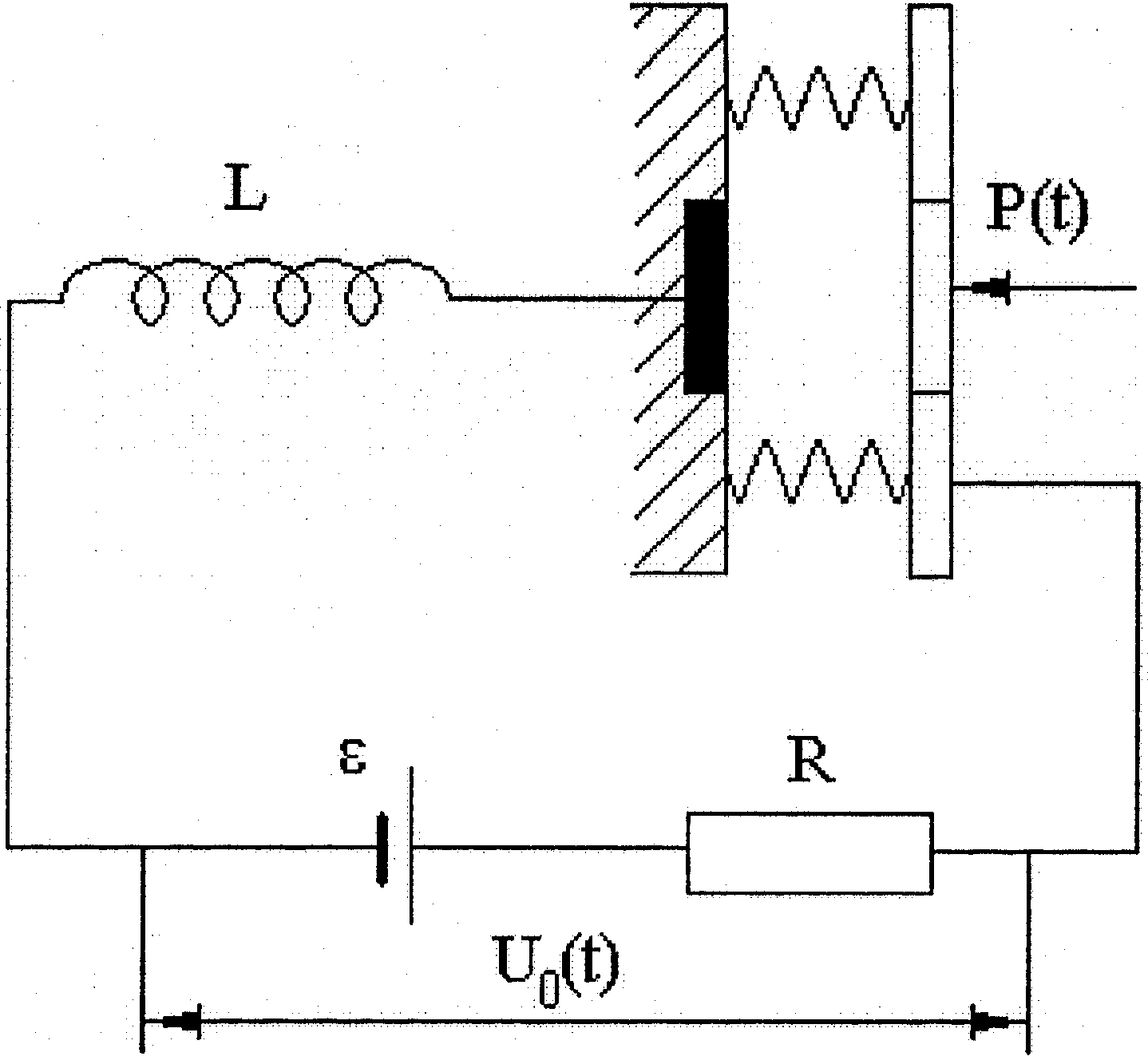
Рис. 5. Схема конденсаторного микрофона

Емкость конденсатора изменяется при колебаниях диафрагмы от звуковых волн. В результате изменяется сила тока в цепи и выходное напряжение , которое и обеспечивает в дальнейшем воспроизведение звука.

За первую обобщенную координату смешанной системы примем величину смещения подвижной пластины от положения равновесия , когда звуковое давление равно нулю (рис. 6). Если в положении пружины сжаты на длину , то в произвольном положении величина сжатия равна , а расстояние между пластинами .

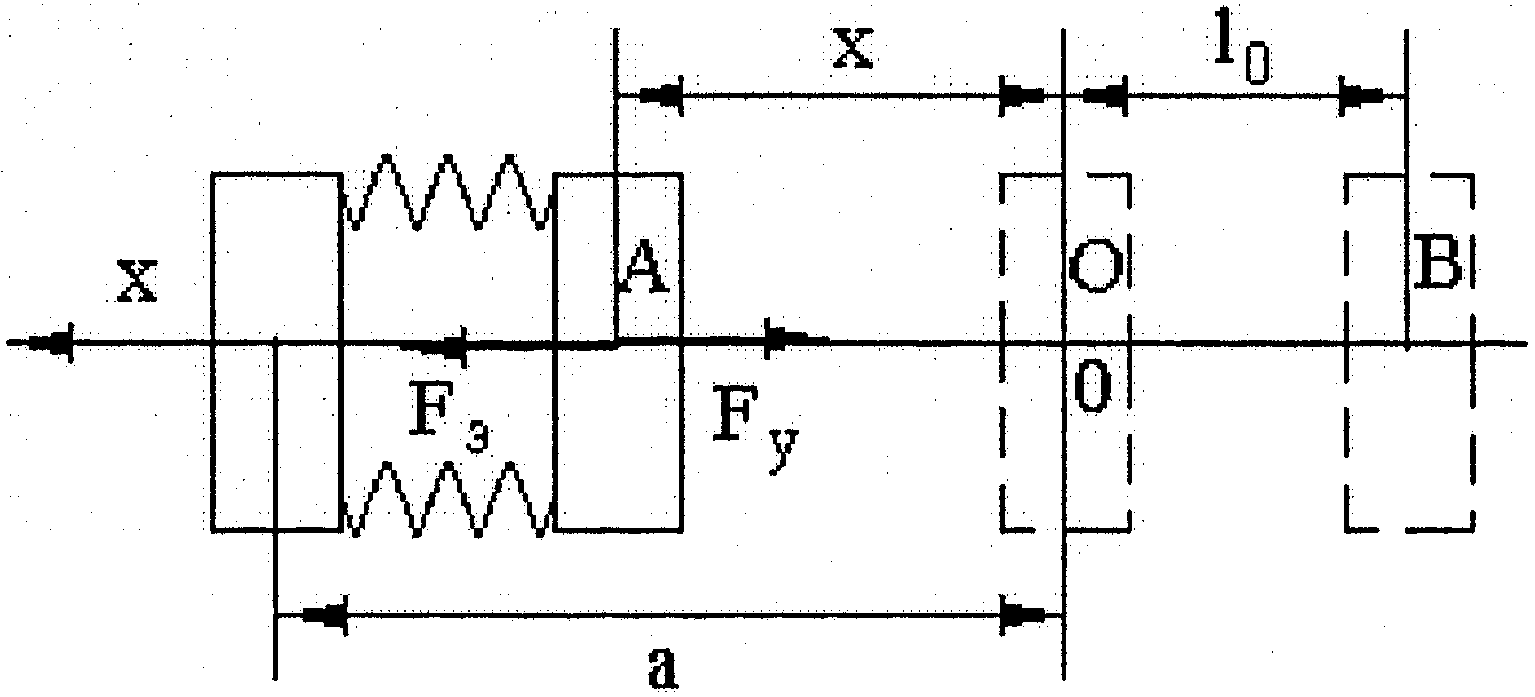
Рис. 6. Выбор координаты : – произвольное

положение подвижной пластины, – положение

подвижной пластины при несжатых пружинах,

– начало отсчета, соответствующее условию

Емкость конденсатора обратно пропорциональна расстоянию между пластинами:

.

В положении равновесия при , отсюда получаем и

.

Полный заряд конденсатора равен

,

где – отклонение заряда от величины в равновесии при отсутствии звукового давления. Величину примем за вторую обобщенную координату.

Обобщенные кинетическая и потенциальная энергии системы

,

.

Функция Релея

.

Вынуждающие обобщенные силы

,

Составляем для системы уравнения Лагранжа:

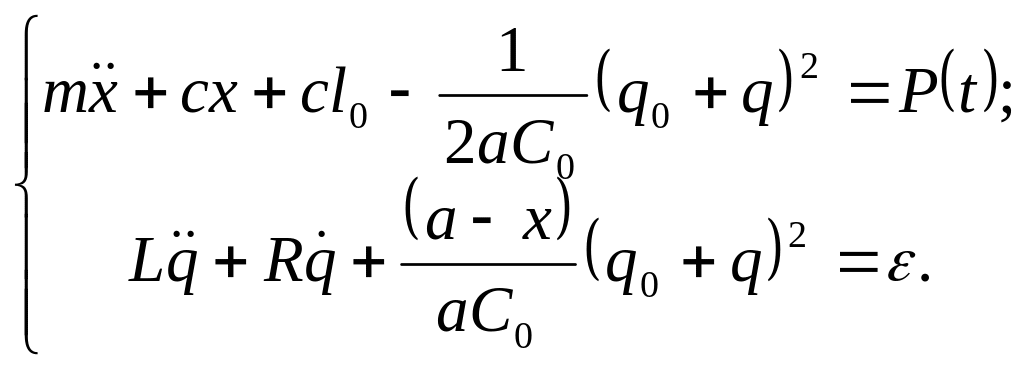
Эти уравнения можно упростить, если учесть начальные условия: в положении равновесия , , , , . Получаем: