Глава 2. Формальная классификация абстрактных автоматов и их математические модели.

2.1 Словесные определения автоматов.

Формализации (представлению в математической форме) любого понятия предшествует попытка словесного выражения (определения) данного понятия. В этой связи представляет интерес проследить трансформацию во времени словесных определений понятия "автомат".

В энциклопедии "Просвещение" 1900 года издания дается следующее определение (определение 1): "Автомат – прибор, помощью внутреннего механизма подражающий действиям живых существ". Из данного определения следует, что автомат - материальный объект (т.к. прибор); внутри этого материального объекта находится некий механизм; этот механизм действует так, что поведение автомата в целом похоже на действия каких - то живых существ. В соответствии с рассмотренным определением попытаемся выяснить: являются ли механические часы автоматом? Часы - материальный объект; внутри часов работает механизм, отсчитывающий время. Но, действиям какого живого существа подражают обыкновенные механические часы? Таким образом, в соответствии с рассмотренным определением обыкновенные механические часы не могут быть названы "автоматом", т.к. они не подражают действиям какого-либо живого существа.

Р

14

13

ассмотрим модификацию механических часов, которые кроме часового механизма снабжены еще дополнительным механизмом. Таким механизмом может быть петушок, кукарекающий каждый раз, когда часы показывают какое-либо определенное время. В таком случае часы, с кукарекающим через определенные интервалы времени петушком, могут быть отнесены, по определению, к автоматам. Но кукарекать петушка можно "заставить" и без часов, которые отмеривают реальное время. Следовательно, действительным автоматом, по определению, является только кукарекающий петушок. А что если внутри кукарекающего петушка будут отсутствовать механические детали? Можно ли в таком случае отнести такого петушка к автоматам?

Как видно, рассмотренное определение автомата несколько противоречиво, и достаточно широкое, так как "живых существ" - огромное множество, включая и человека.

Рассмотрим некоторые последующие словесные определения автомата, не вдаваясь в достаточно глубокий их анализ.

В [8] (1963 год) дается следующее определение (определение 2).

Автомат (от греческого automatus - самодействующий) - рабочая машина, самостоятельно производящая все рабочие, холостые, транспортирующие и др. движения и осуществляющая управление этими движениями.

В [9] (1980 год) еще более уточняется понятие автомата (определение 3).

Автомат (от греческого automatus - самодействующий)

1. устройство (совокупность устройств), выполняющее по заданной программе без непосредственного участия человека все операции в процессах получения, преобразования, передачи и распределения (использования) энергии, материалов или информации. Программа автомата задается в его конструкции или извне - посредством перфокарт, магнитных лент и т.п.;

2. в кибернетике: математическая модель устройства (процесса), перерабатывающего дискретную (цифровую) информацию.

В [10] (1988 год) приводится следующее определение (определение 4).

1. Автомат – устройство, предназначенное для выполнения целенаправленных действий без непосредственного участия человека.

2. Автомат абстрактный – математическая модель автомата по п.1, определяемая заданием трех множеств (входных сигналов, внутренних состояний и выходных сигналов) и двух двуместных функций (переходов и выходов). Функция переходов отображает первые два множества на второе, а функция выходов отображает первые два множества на третье.

3. Автомат структурный – автомат абстрактный, по п.2, заданный множеством его элементов и схемой их соединения.

Последнее словесное определение дает возможность перейти к формальному определению понятия автомата.

2.2 Формальное определение абстрактного автомата.

Математической моделью дискретного устройства является абстрактный автомат, определяемый как шестикомпонентный кортеж, или вектор [11]:

S = (Z, A ,W, δ, λ, a₁), (2.1)

у которого:

Z={z₁,…z_f…z_F} - множество входных сигналов автомата (входной алфавит);

A={a₁,…a_m…a_M} - множество состояний автомата (алфавит состояний);

W={w₁,…w_g…w_G} – множество выходных сигналов автомата (выходной алфавит);

δ : A х Z  A – функция переходов автомата, реализующая отображение D_δ A х Z на A. Другими словами, функция δ некоторым парам состояние - входной сигнал (a_m, z_f) ставит в соответствие состояние автомата a_s = δ (a_m, z_f), a_s A;

λ : A х Z  W – функция выходов, реализующая отображение D_ A х Z на W, которая некоторым парам состояние - входной сигнал (a_m, z_f) ставит в соответствие выходной сигнал автомата w_g = λ (a_m, z_f);

a₁ A – начальное состояния автомата.

П

16

15

од алфавитом здесь понимается непустое множество попарно различных символов. Элементы алфавита называются буквами, а конечная упорядоченная последовательность букв - словом в данном алфавите.

Абстрактный автомат имеет один вход и один выход. Автомат работает в дискретном времени, принимающем целые неотрицательные значения t = 0,1,2,… В каждый момент t дискретного времени автомат находится в некотором состоянии a(t) из множества состояний автомата, причем в начальный момент времени t(0) автомат может находиться в начальном состоянии a(0) = a₁. В момент t, будучи в состоянии a(t), автомат способен воспринять на входе букву входного алфавита z(t) Z. В соответствии с функцией выходов он выдает в тот же момент времени t букву выходного алфавита w(t) = λ (a(t)_, z(t)) и в соответствии с функцией переходов перейдет в следующее состояние a(t +1) = δ (a(t)_, z(t)), причем a(t +1) A, а w(t) W. Смысл понятия абстрактного автомата состоит в том, что он реализует некоторое отображение множества слов входного алфавита Z в множество слов выходного алфавита W. Иначе, если на вход автомата, установленного в начальное состояние a₁, подавать буква за буквой некоторую последовательность букв входного алфавита z(0), z(1), z(2), … - входное слово, то на выходе автомата будут последовательно появляться буквы выходного алфавита w(0), w(1), w(2), … - выходное слово. Каждому входному слову соответствует определенное выходное слово, структура которого определяется функциями переходов и выходов.

Таким образом, на уровне абстрактной теории понятие "работа автомата" понимается как преобразование входных слов в выходные слова. Структурной моделью нулевого уровня абстрактного автомата является модель, представленная на рис. 2.1.

S

Z W

Рис. 2.1. Структурная модель абстрактного автомата

(нулевой уровень)

В том случае, когда отображения D_ = D_ = A х Z, автомат называют полностью определенным или полным. Иными словами, у полностью определенного автомата области определения функций δ, λ совпадают с множеством A х Z – множеством всевозможных пар вида (a_m, z_f). У не полностью определенного, или частичного, автомата функции δ или λ определены не для всех пар (a_m, z_f) A х Z.

Состояние частичного автомата, соответствующее паре (a_m, z_f), на котором функция переходов не определена, называют неиспользуемым состоянием автомата. Остальные состояния называют используемыми [5].

Если на каком-либо используемом состоянии автомата не определена функция выходов, то говорят, что этому состоянию соответствует безразличное состояние выхода. В частном случае может быть безразличным не состояние выхода, а лишь один или несколько выходных сигналов, набор значений которых определяет данное состояние выхода [5].

Чтобы задать конечный автомат S, необходимо описать все компоненты вектора S = (Z, A ,W, δ, λ, a₁), т.е. входной и выходной алфавиты и алфавит состояний, а также функции переходов и выходов. Среди множества состояний может быть выделено начальное состояния автомата a₁, в котором автомат находится в момент t = 0.

2.3 Формальная классификация автоматов

Один из способов классификации абстрактных автоматов состоит в рассмотрении мощностей множеств A, Z, W и общих свойств функций переходов δ и выходов λ, которые также называют характеристическими [1], [2], [13].

1. Автомат инициальный - автомат, для которого задано a₁ (начальное состояние) и который всегда начинает функционировать с этого состояния;

2. А

   18

   17

   втомат не инициальный - автомат, для которого в качестве начального состояния может быть взято

любое из допустимых его состояний A={a₁,…a_m…a_F};

3. Автомат конечный - автомат, у которого одновременно конечны множества входного, выходного алфавитов и алфавита состояний, т.е. , 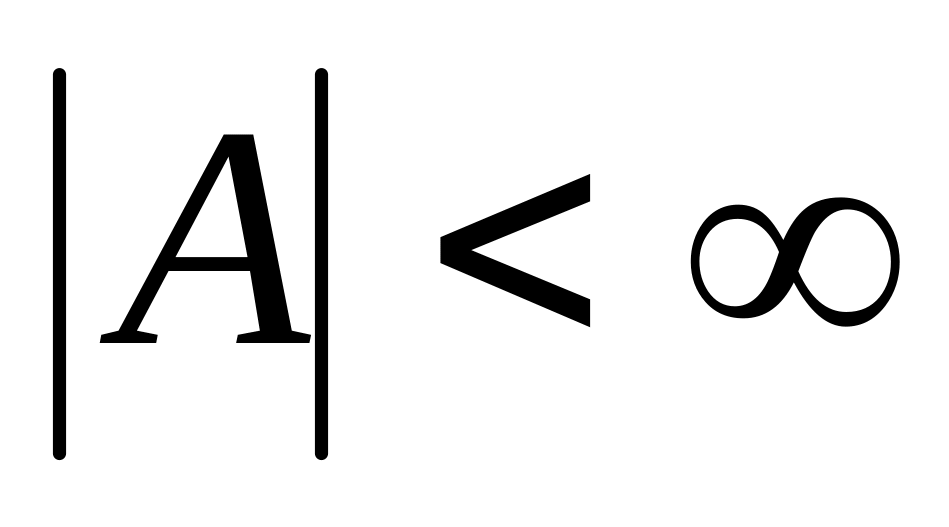и ;

4. Автомат бесконечный - автомат, у которого бесконечны хотя бы одно из множеств входного, выходного алфавитов или алфавита состояний, т.е. , или , или ;

5. Автомат без памяти (комбинационный автомат) - автомат, у которого множество состояний состоит из одного элемента, т.е. . Для такого автомата характерно то, что функция переходов вырождается (отсутствует), а функция выходов однозначно определяет выходной символ как некоторую функцию от входного символа, т.е. W= λ(Z);

6. Автомат без входов (автономный автомат) - автомат, у которого множество входных символов состоит из одного элемента 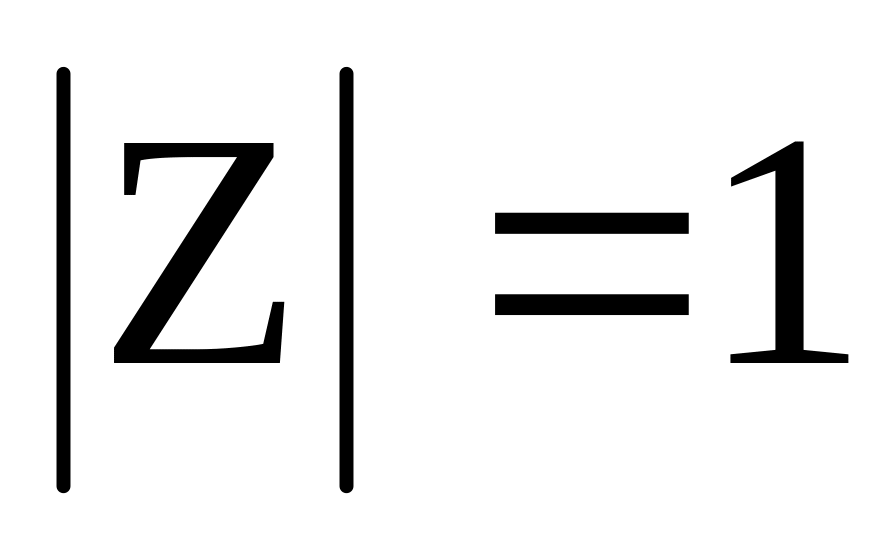, т.е. автомат не имеет входов или, что то же самое, состояние его входа (входной символ) имеет неизменное значение, и функционирование автомата не зависит от входных символов. В этом смысле говорят, что автономный автомат является автоматом без входов. Для таких автоматов характерно то, что следующее состояние автомата и его выходной символ однозначно определяется только состоянием автомата в данный момент времени;

7. Автомат без выхода (распознаватель) - автомат, у которого множество выходных символов состоит из одного символа. Поведение автомата без выхода можно охарактеризовать тем, как последовательность входных символов перерабатывается в последовательность внутренних состояний автомата. Иногда поведение автомата без выхода рассматривают как поведение устройства, воспринимающего вопросы и дающего на них ответы "да" или "нет";

8. Детерминированный автомат - автомат, для которого функции переходов и выходов являются всюду определенными (однозначными) функциями;

9. Недетерминированный автомат - автомат, для которого допускаются многозначные функции переходов и выходов, т.е. при данных входном символе и внутреннем состоянии автомат может переходить в несколько различных состояний;

10. Вероятностный автомат - автомат, в котором функции переходов и выходов являются случайными функциями. Они задаются матрицей переходных и выходных вероятностей, в соответствии с которой при входном символе будет выбираться выходной символ и следующее состояние автомата;

11. Нечеткие автоматы - автоматы, для которых функции переходов и выходов заменяют нечеткими отношениями. Нечеткие автоматы являются математическими моделями некоторых распознающих устройств и используются в задачах распознавания образов.

2.4 Математические модели автоматов

Все существующие математические модели автоматов можно разделить на общие и специализированные модели, что отражает многообразие разновидностей автоматов.

К

20

19

общим моделям относят модели Мили и Мура, названные по имени впервые исследовавших эти модели американских ученых G.H. Mialy и E.F. Moore, а также модель С-автомата, которая является совмещением моделей Мили и Мура.

Из специализированных моделей, получившей распространение в автоматике и вычислительной технике, наиболее известна и широко используется модель микропрограммного автомата, как композиция управляющего автомата и операционного автомата.

2.4.1 Модель Мили.

Закон функционирования автомата типа Мили математически задается следующей системой уравнений (2.2):

, (2.2)

где

a(t) – внутреннее состояние автомата в момент времени t (настоящий момент времени);

z (t) – входной сигнал в момент времени t;

w (t) – выходной сигнал в момент времени t;

a (t+1) - внутреннее состояние автомата в момент времени (t+1) (в следующий момент времени);

δ - функция переходов;

λ - функция выходов.

Первое уравнение в (2.2) отражает тот факт, что переход автомата в следующее состояние a(t+1) осуществляется только с приходом входного сигнала (входного символа) z(t) в момент времени t. При этом, то конкретное состояние, в которое перейдет автомат в момент времени (t+1), определятся парой (a_m, z_f), т.е. состоянием автомата a(t) и входным сигналом (символом) z(t) в момент времени t.

Второе уравнение в (2.2) отражает закономерность формирования выходного сигнала (символа) автоматом типа Мили. Из уравнения видно, что выходной сигнал формируется автоматом в тот же момент времени t, в который действует входной сигнал z(t) и только до тех пор, пока автомат не перейдет в новое состояние a(t+1). Конкретное значение выходного сигнала (символа) однозначно определяется парой (a_m, z_f), т.е. состоянием автомата a(t) и входным сигналом (символом) z(t) в момент времени t. Если автомат Мили перейдет в неиспользуемое состояние a(t+1), на котором функция переходов не определена, или в устойчивое состояние, из которого не возможен выход под действием такого же входного сигнала, как и действующего в момент времени t, то и с математической, и с технической точек зрения модель Мили корректна.

Возможна, также ситуация, при которой автомат под воздействием входного сигнала z(t) должен перейти в некоторое состояние a(t+1), из которого под воздействием такого же сигнала возможен переход в другое состояние автомата. В этом случае промежуточное состояние автомата будет неустойчивым (автомат его "проскочит"), если длительность входного сигнала будет превышать время переходного процесса в автомате (т.е. время перехода автомата из одного состояния в другое). Из данных рассуждений следует, что математическая и техническая корректность модели Мили обеспечивается только в том случае, если допустить, что длительность входного сигнала столь мала, что не превосходит времени переходных процессов в автомате. Но тогда, как следует из второго уравнения (2.2), длительность выходного сигнала будет не больше длительности входного сигнала и, следовательно, выходной сигнал в автомате Мили будет таким же "коротким", как и входной сигнал.

Характерной особенностью автомата типа Мили является также и то, что он "не помнит" предшествующей последовательности своих состояний и "не знает" своих последующих действий, отдаленных более чем на один такт автоматного времени. Данная особенность характерна и для большинства разновидностей дискретных автоматов, в том числе и для автоматов типа Мура, С-автоматов и микропрограммных автоматов.

22

21

2.4.2 Модель Мура.

Закон функционирования автомата типа Мура математически задается следующей системой уравнений (2.3):

, (2.3)

где

a(t) – внутреннее состояние автомата в момент времени t (настоящий момент времени);

z (t) – входной сигнал в момент времени t;

w (t) – выходной сигнал в момент времени t;

a (t+1) - внутреннее состояние автомата в момент времени (t+1) (в следующий момент времени);

δ - функция переходов;

λ - функция выходов.

Первое уравнение в (2.3) отражает тот факт, что переход автомата в следующее состояние a(t+1) осуществляется только с приходом входного сигнала (входного символа) z(t) в момент времени t. При этом, то конкретное состояние, в которое перейдет автомат в момент времени (t+1), определятся парой (a_m, z_f), т.е. состоянием автомата a(t) и входным сигналом (символом) z(t) в момент времени t. Функция переходов в автомате типа Мура имеет такой же вид, как и для автомата типа Мили со всеми рассмотренными ранее особенностями математической и технической корректности модели.

Второе уравнение в (2.2) отражает закономерность формирования выходного сигнала (символа) автоматом типа Мура. Из уравнения видно, что выходной сигнал определяется только состоянием автомата в момент времени t и в явном виде не зависит от входного сигнала z(t). Соответствующий состоянию a(t) выходной сигнал в автомате Мура формируется на всем протяжении времени, пока автомат находится в состоянии a(t). В связи с данной особенностью автомата типа Мура говорят, что данный тип автомата формирует "длинные" выходные сигналы, которые однозначно определяются тем состоянием автомата, в котором он находится в данный момент времени.

Не смотря на то, что состояние выхода автомата Мура не зависит явно от состояния входа, его можно рассматривать как частный случай автоматов Мили. Действительно, так как для автоматов Мура справедливо

a(t) = δ (a(t-1), z(t-1)), (2.4)

то справедливо и следующее соотношение:

w(t) = λ (a(t)) = g (a(t-1), z(t-1)). (2.5)

Соотношение (2.5) показывает, что в автомате Мура выходной сигнал реально зависит от входного сигнала, но только действующего в предыдущий момент времени. Различие между автоматами Мура и Мили состоит в том, что в автоматах Мили выходной сигнал возникает одновременно с вызывающим его входным сигналом, а в автоматах Мура - с опозданием (задержкой) на один такт автоматного времени. Поэтому автоматы Мура можно рассматривать как автоматы Мили, имея в виду, что последовательность состояний выхода автомата Мили опережает на один такт последовательность состояний выхода автомата Мура.

В теории автоматов доказано [11], что между автоматами Мили и Мура существует взаимооднозначное соответствие: любой автомат Мили может быть преобразован в эквивалентный ему автомат Мура и наоборот.

П

24

23

ри переходе от автомата Мура к автомату Мили число состояний автомата не меняется, тогда как при обратном переходе число состояний в автомате Мура, как правило, возрастает. Таким образом, эквивалентные между собой автоматы могут иметь различное число состояний, в связи с чем в теории автоматов возникает задача нахождения минимального (с наименьшим числом состояний) автомата в классе эквивалентных между собой автоматов.

Существование для любого абстрактного автомата эквивалентного ему абстрактного автомата с минимальным числом внутренних состояний впервые было доказано Муром.