Учебное пособие 800545

(некогерентный прием): ui(t)=Aicos[ it+ i(t)+ ], t [0, Т], i=1, 2. Решение данной задачи подробно описано в [1]. Для сравнения, зависимость Рош от q2 для различных типов полезных сигналов при некогерентном приеме показана на рис. 3.13 пунктиром. Как видно из рисунка при ЧМН и АМН помехоустойчивость некогерентного приема хуже, чем когерентного. ФМН-сигналы в схеме некогерентного приема неразличимы. В общем случае наибольшую помехоустойчивость имеет фазовая манипуляция при когерентном приеме.

IV. ОПТИМАЛЬНАЯ ОЦЕНКА ПАРАМЕТРОВ СИГНАЛОВ

§ 4.1. Задача оптимальной оценки параметров сигналов

Часто пользователю для извлечения нужных сведений необходимо измерить (оценить) значения тех или иных параметров сигнала. Термин ―оценка‖ применяется для обозначения как самого процесса измерения параметра, так и его результата. Полученные в результате оценки значения параметров не обязательно точно воспроизведут истинные, так как в реальных условиях полезный сигнал поступает на вход РПУ в смеси с помехами и содержит не только несущие нужную информацию полезные (информационные) параметры, но и параметры, не содержащие нужной информации (неинформационные). В целях общности все параметры будем обозначать символом , а их оценку — величиной .

Так как неизвестна, то она будет рассматриваться как случайная

оценки параметров дана в § 2.2. Априорная плотность вероятности W( ) может быть как известной, так и неизвестной наблюдателю.

Решение задачи оценки параметров предполагает предварительный выбор критерия оптимальности. В результате решения должна быть получена структура оптимального измерителя и определена дисперсия оценки. Методы решения этой задачи базируются на методах математической статистики. Оценка может производиться как по выборкам входного процесса x(t), так и по непрерывным реализациям. В последнем случае оценка будет более точной.

К измеряемым параметрам в РТС относят время прихода сигнала, его длительность, частоту, начальную фазу и т.д. Оценка параметров сигналов будет производиться в предположении, что полезный сигнал на входе РПУ обязательно присутствует. Все параметры сигнала делятся на энергетические и неэнергетические. К энергетическим относят те, от которых зависит отношение сигнал/шум q2=q2( ). Это амплитуда и длительность сигнала. Остальные параметры (частота, фаза и т.п.) относят к неэнергетическим. Ниже мы будем рассматривать только неэнергетические параметры.

Если принимает дискретные значения из конечного множества размерностью М, то задачу оценки дискретного параметра можно рассматривать как различение М сигналов. Очевидно, что от данного

170

случая возможен переход и к измерению непрерывного параметра [1]. В силу этой взаимосвязи в первую очередь будем рассматривать только оценку непрерывного параметра.

Процесс оценки параметров сопровождается ошибками. Ошибки делятся на грубые промахи, систематические и случайные. Если есть

источник систематической ошибки, то есть смещение оценки 0 , то оценка называется смещенной, в противном случае — несмещенной. Ниже мы будем рассматривать только случайные ошибки одного параметра сигнала, обусловленные действием помех.

Для характеристики качества измерителя будем использовать

2

качественным показателем измерителя, который всегда стремятся уменьшить: D [ ] 2 D min . В этом случае измеритель и оценка

называются измерителем и оценкой с минимальной дисперсией. В последней формуле приведены различные обозначения дисперсии.

Доказано, что дисперсия любой оценки при некоторых условиях не может быть ниже границы, определяемой неравенством Рао-Крамера, которое для несмещенных оценок имеет вид:

нижней границе этого неравенства, называют эффективной. Эффективностью оценки параметра называют отношение

дисперсии эффективной оценки к дисперсии рассматриваемой оценки. При оценке параметров возможны две ситуации: 1) априорная

плотность вероятности W( ) известна; 2) W( ) неизвестна. Ниже мы будем рассматривать только первый случай.

При оценке параметров с известной априорной W( ) используется байесовский подход. Он основан на минимизации среднего риска ошибки измерения:

171

Если средний риск r[ , * ] минимален, то измерение является

наилучшим. Оценка, минимизирующая r[ , * ], называется оптимальной

байесовской оценкой. На основе байесовского критерия (4.2) при решении конкретных задач можно строить различные правила оценки, которые рассматриваются в следующем разделе.

§ 4.2. Байесовская оценка неэнергетических параметров сигнала

Рассмотрим на примере задачи оптимального измерения неэнергетических параметров сигнала, как на основе байесовского подхода формируются правила оценки.

Пусть параметр i полезного сигнала u(t, 1n ) является измеряемой

случайной величиной с априори известной плотностью вероятности W( i). Требуется с минимальной погрешностью восстановить значение

Изложенный ниже подход к оценке параметров справедлив для случая q21, где q2=2Е/N0 .

Для решения задачи используем байесовский подход (4.2). Если = (x), то, в соответствии с преобразованием двумерной случайной

172

Из данного выражения видно, что r[ , *(х)] будет минимальным,

если при любом значении величины х оценка (x) выбрана таким образом, что имеет место минимум внутреннего интеграла. Значит, от критерия минимального среднего риска можно перейти к критерию минимального условного среднего риска:

привести к различным результатам измерений по критериям (4.2) и (4.3).

условного среднего риска не достигается. Чтобы он был обеспечен,

Рис. 4.1. Выбор оценки на основании критерия минимального условного среднего риска и квадратичной функции стоимости r[ , ]

Математически задача минимизации условного среднего риска решается путем нахождения его экстремума:

173

Преобразовав квадрат разности и продифференцировав левую часть

Из последнего выражения находим:

последнее правило широко применяют на практике. Его называют

принципом максимума апостериорной вероятности.

Условная плотность вероятности W( /x) имеет фундаментальное значение в теории радиосвязи — если она известна, то не надо иметь

Часто при определении W( /x) встречаются значительные трудности. К более простым результатам можно прийти, если априорная

распределение х, которое обычно известно. Исходя из формулы Байеса и условия нормировки

174

Синтез устройств оптимальной оценки параметров по правилу максимума корреляционного интеграла (4.8) производится с учетом результатов, полученных в §§ 3.1, 3.2, 3.5. При этом будем считать, что постановка задачи оценки позволяет применять принцип (4.8).

Из (3.26) следует, что для смеси нормального белого шума и сигнала u(t, ) функционал правдоподобия имеет вид:

нужно иметь множество значений Z(x/ ) в зависимости от значений . Поэтому схемы оптимальных измерителей должны быть многоканальными. Как всегда, возможны две схемы устройств оптимальной оценки параметров. Корреляционная схема приведена на рис.

4.2.

Рис. 4.2. Корреляционная схема устройства оптимальной оценки параметра

В каждом из каналов вычисляется степень схожести реализации х(t) и копии сигнала с параметром i. Решение выносится по максимальному оклику канала. Значение параметра i копии сигнала в канале, давшем

неопределенности по координате (будет подробнее рассмотрен в главах

V, IX) [15].

Схема фильтрового приемника аналогична приведенной на рис. 4.2, только вместо корреляторов устанавливаются фильтры, каждый из которых согласован со своим вариантом полезного сигнала u(t, i), i=1, 2,..., l.

176

Иногда используются одноканальные, перестраиваемые во времени, cхемы оценки параметра. В них параметр копии сигнала 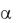меняется во времени до достижения максимального отклика коррелятора. Данные схемы проще многоканальных, но требуют существенно большего времени анализа, а это определяет и существенно большую длительность наблюдения сигнала. Многоканальные схемы обычно называют параллельными схемами анализа, а одноканальные — последовательными.

На основе приближенного решения уравнения (4.8)

можно получить схемы дифференциального типа (рис. 4.3):

Рис. 4.3. Схема дифференциального типа устройства оптимальной оценки параметра

Здесь у опорных сигналов изменяется во времени до получения нулевого сигнала на выходе. Соответствующее ему значение 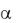и есть оптимальная оценка опт .

Основной характеристикой измерителя является дисперсия оценки

177