Добавил:

mihail1000 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Учебное пособие 800514

.pdf

Скачиваний:

Добавлен:

01.05.2022

Размер:

3.99 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 910 / 1410 11 12 13 14 > Следующая >>>

3) f 01110010 ;	6) x	y	y z .

4.Построить полиномы Жегалкина для элементарных булевых функций.

5.При помощи эквивалентных преобразований построить полиномы Жегалкина для следующих функций:

1) D xy yz xz ; 4) D x z xyz ;

2) D x1 x2		x2 x4	x3 ;	5) D x1 x2		x1 x2 x3			x3 ;
3) D	xyz	x z		6) D	xyz	x .
6.	Наборы ~		~	,..., ~	и ~	~	,...,	~	на-
			1	n		1		n

зываются соседними, если они отличаются только одной координатой. Доказать, что если функция f x1 ,..., xn на двух со-

седних наборах принимает противоположные значения, то она линейная. Верно ли обратное утверждение?

7.Выяснить, является ли линейной функция f :

1)	f	x1 x2 x1	x2	;	3)	f	01011001 ;
2)	f	x ~ y y		z	~ z ; 4)	f	0110100110100101 .
				2.7.2 Замкнутость
	Обозначим множество всех булевых функций через Б.
Пусть		f x1 ,..., xn	,	g1	x1 ,..., xm		, …, gn x1 ,..., xm - про-

извольные булевы функции. Суперпозицией этих функций называется функция

	x1 ,..., xm		f	g1 x1 ,..., xm ,..., gn	x1 ,..., xm .
Пример		1.	Пусть	f x1 , x2 , x3	x1 ~ x2	x3 ,

g1 x, y	xy ,	g2	x, y	x , g3 x, y x	y , тогда их су-
перпозиция			x, y	реализуется	формулой

xy ~ x	x	y .

Пусть М - некоторое множество булевых функций:

МБ . Замыканием М множества М называется сово-

купность всех тех булевых функций, которые являются суперпозициями функций из множества М . Операция получения

множества М из М называется операцией замыкания.

Множество М называется	функционально замкнутым клас-
сом (короче, замкнутым	классом), если М	М . Таким

образом, замкнутый класс вместе с любыми его функциями содержит и все их суперпозиции.

Традиционно выделяют пять замкнутых классов булевых функций:

1.Класс L линейных функций.

2.Класс T0 булевых функций, сохраняющих константу 0:

			T0	f	Б \|	f 0,...,0		0 .
Функции x & y, x				y, x	y, x являются функциями из T0 ,
тогда как x \| y,			x	y, x	y, x ~ y, x не принадлежат T0 .
3.	Класс T1	булевых функций, сохраняющих константу 1:
			T1	f	Б \|	f 1,...,1		1 .
	Как легко проверить,				x y, x & y, x			y, x ~ y, x, 1
– функции из T1 , в то время как						x \|	y, x	y, x	y, x, 0 не
принадлежат T1 .
4.	Класс	S	самодвойственных				функций.		Функция
f	x1 ,..., xn	называется самодвойственной, если она совпа-
дает со своей двойственной:
	S		f	Б \| f	x1 ,..., xn		f	x1 ,..., xn .
	Очевидно,		что	самодвойственными				функциями будут
x, x ; функции			x	y, xy, x		y,	x \| y не являются само-

двойственными.

Пример 2. Покажем, что функция

x, y, z

yz является самодвойственной. Дей-

ствительно,

x, y, z

xyz

xy xz yz

xy 1

zy.

Для самодвойственной функции имеет место тождество

x1 , ..., xn

f x1 , ..., xn ,

1 ,...,

так что на наборах

1 ,...,

, которые мы бу-

дем называть противоположными, самодвойственная функция принимает противоположные значения.

Пример 3. Функция f1 x, y, z01101110 не явля-

ется самодвойственной, так как на противоположных наборах (000) и (111) она принимает одно и то же значение 0.

Функция f2 x, y, z 10110010 является самодвой-

ственной, так как на каждой паре противоположных наборов она принимает противоположные значения.

Справедливо следующее утверждение, называемое обыч-

но леммой о несамодвойственной функции:

	Если функция f x1 ,..., xn						несамодвойственная, то, под-
ставляя на места ее переменных							x и x , можно получить кон-
станту.
5. Класс M монотонных функций.
	Говорят, что набор					~	,...,	n	предшествует набору
						1		n
~	1	,...,		n	и пишут ~		~ , если		i	i	, i 1,..., n .
	1			n					i	i
Функция			f	x1 ,..., xn		Б называется			монотонной, если
f ~		f	~	при ~		~ .

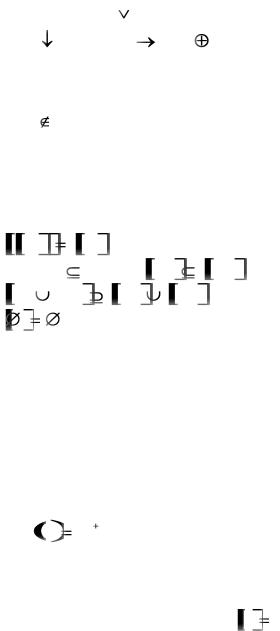
Функции x, 0, 1, x y, xy являются монотонными, то-

гда как x, x y, x | y, x

y, x y, x ~ y не принадле-

жат классу M .

Справедливо утверждение (лемма о немонотонной функции):

Если f M , то, подставляя на места ее переменных 0, 1, x , можно получить функцию x .

ЗАДАЧИ И УПРАЖНЕНИЯ

1.Обосновать следующие свойства замыкания:

1)	M	M ;
2)	если M1		M2 , то	M1	M2 ;
3)	M1	M2	M1	M2	;
4)		.

2.Всегда ли на множестве Б булевых функций:

a)пересечение замкнутых классов является замкнутым классом;

b)разность замкнутых классов есть замкнутый класс;

c)дополнение замкнутого класса не является замкнутым классом?

3.	Показать, что суперпозиция линейных функций
является линейной		функцией, т.е. что класс L замкнут, и
мощность	L n	2n 1 , где n- число переменных.

4.Показать, что классы T0 и T1 функций, сохра-

няющих константу, замкнуты.

5.Показать, что суперпозиция самодвойственных

функций является самодвойственной, т.е. S

S .

6.Доказать замкнутость класса монотонных функ-

ций.
7.		Показать,		что мощности множеств T0		n и
T1 n	функций от n переменных, сохраняющих константы,
совпадают:		T n	T	n	22n 1.
совпадают:		T n	T	n	22n 1.
		0	1
8.		Показать,		что мощность множества S n		само-

двойственных функций от n переменных вычисляется по

		22n .
формуле:	S n

9.Самодвойственна ли функция f ?

1)	f	x		y	xz	yz ;
2)	f	x	y	z t	xyz ;
3)	f	x	y	y	z z	x ;

4)f 01011110 ;

5)f 0001001001100111 .

10. Из несамодвойственной функции f с помощью под-

становки на места переменных функций x и x получить константу:

1) f 00111001 ;

2) f x y z t xyz;

3)	f	x	y	x	z ;
4)	f	xy	xz	yt	z t .
11. Выяснить, каким из множеств T0						T1 ,T1 \ T0 при-
надлежат перечисленные ниже функции:
1)		x y		x \| yz	y ~ z	x ;
2)	xy		z \|	x z	z xy .

12. Сколькими способами можно расставить скобки в выражении x1 x2 x1 x2 x1 , чтобы получилась

формула, реализующая функцию из T0.

13.Подсчитать число функций, зависящих от переменных x1 , x2 ,..., xn , в каждом из следующих множеств:

1)T1 T0 ;

2)T0 L;

3)T1 L;

4)L \ T0 T1 ;

5)T1 S;

6)L S T1 ;

7)S T0 T1 ;

8)T0 T1 ;

9)S \ T0 T1 ;

14.Найти функцию f x,..., x , если:

1)	f x1		..., xn	T1 \ T0 ;
2)	f	x1	,..., xn	L \ T1 S ;
3)	f	x1	,..., xn	S \ T0 ;

15.Какие из перечисленных ниже функций являются монотонными:

1)	x	x	y ;
2)	x	y	x ;
3)	xy x		y ;
4)	xy	yz	zx x;
5)	f	00110111 ;

6) f 011001111 ;

7) f 0001010101010111 ;

	8) f	0000000010111111
16.	Сколько		существует	таких монотонных функций
f x, y, z ,		что	f 0,1,1	f 1,0,1	1, f 0,0,1 0 ?
Сколько таких функций принадлежит множеству M \ S ?
17.	Показать, что если f			M , то f *	M.
18.	Показать,		что замкнутые классы T0 ,T1 , S, M, L по-

парно различны.

2.7.3 Полнота

Для всякой булевой функции существует представление в виде дизъюнктивной или конъюнктивной нормальных форм. Отсюда следует, что всякая функция f Б может быть вы-

ражена в виде формулы через элементарные функции: отрицание x , дизъюнкцию x y и конъюнкцию x y . В связи с

этим возникает вопрос: существуют ли другие системы булевых функций, которые обладают таким же свойством? Ответом на этот вопрос являются приводимые ниже понятия и теоремы.

Система булевых функций F f1 , f2 , ..., f S , ... назы-

вается полной, если любая булева функция может быть записана в виде формулы через функции этой системы, другими словами, является суперпозицией функций из системы F .

Из этого определения следует, что система F полна, ес-

ли F	F . Рассмотрим примеры полных систем:
1.	Система F	x, x y, x y представляет

собой полную систему.

2.Система F x y, x & y, 0, 1 также полна,

так как любая булева функция представима в виде полинома Жегалкина;

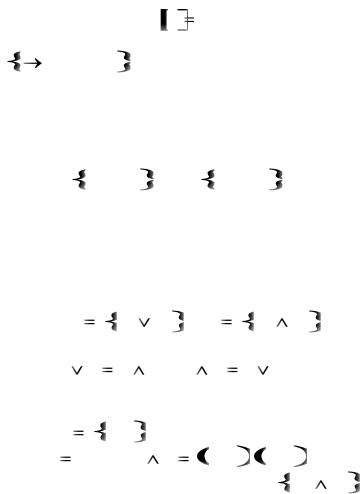
3.Множество Б всех булевых функций также об-

разует полную систему, так как		Б Б .
Ясно, что не всякая система является полной. Например,
система x	y, x & y не	является полной. Следующая

теорема позволяет сводить вопрос о полноте одних систем к вопросу о полноте других систем.

Теорема (о полноте двух систем):

Пусть даны две системы функций

F f1 , f2 ,... и G g1 , g2 ,... ,

относительно которых известно, что первая система полна в Б и каждая ее функция является суперпозицией функций второй системы. Тогда вторая система также является полной.

Пользуясь этой теоремой, можно доказать полноту еще ряда функциональных систем и тем самым расширить список примеров полных систем.

4. Системы G1	x, x		y и G2	x, x		y	являют-
ся полными. Из равенств

x	y	x	y и x y	x	y
следует, что в качестве системы F можно использовать мно-
жество функций в примере 1.
5. Система G	x \|	y	полна, так как
x x \| x;		x y x \| y \| x \| y
и в качестве F можно взять систему функций					x, x		y из
примера 4.

На множестве Б булевых функций справедлив следую-

щий критерий полноты.

Теорема Поста:

Система F f1 , f2 ,... полна тогда и только тогда,

когда она целиком не содержится ни в одном из замкнутых классов T0 , T1 , S , M , L .

	Применение критерия полноты
	Чтобы исследовать	полноту системы	функций
F	f1 , f2 ,... , удобно	построить следующую	таблицу В

таблице столько строк, сколько функций в данной системе F . В каждую клетку этой таблицы, стоящей на пересечении столбца, соответствующего одному из классов, и строки, соот-

ветствующей функции fi , заносится знак «+», если fi принадлежит этому классу, и знак «-» в противном случае.

В силу критерия Поста для полноты системы F= f1 , f2 ,... необходимо и достаточно, чтобы хотя бы в од-

ной клетке каждого столбца стоял знак «-».

Система (множество) булевых функций называется базисом, если она полна и любая ее подсистема не является полной на множестве булевых функций.

Для выделения базиса из полной системы функций

F	f1 , f2 , f3 ,...	нужно упорядочить по числу функций
множество подсистем системы F:
	f1	, f2 , ..., f1 , f2 , f1 , f3 , ... .

и, начиная с первой, исследовать их на полноту. Первая из полных в этой последовательности подсистем будет базисом.

	Пример.		Исследовать		полноту	системы	функций
F	y	1; x	y; xy	z	и, если она полна, выделить из
нее базис.
	Решение.		Пусть	f1	y 1 ,	f2 xy	z	,
f3	x	y .

			1						2						3

															x
y		y		1	f		x	y		z	xy	f 2	x	y	x	f

0	1			1	0	0		0		0	0	1
0	1			1	0	0		0		0	0	1	0	0	0	1

						0		0		1	0	1

													0	1	1	0

						0		1		0	0	1

													1	0	1	0

						0		1		1	0	1

													1	1	1	0

						1		0		0	0	1
						1		0		0	0	1

						1		0		1	0	1

						1		1		0	1	0

						1		1		1	1	1

Составим таблицы истинности для заданных функций:

T0 T1 S M L

f 2

f 3

…

Исследуем функцию f2 xy		z на принадлежность клас-
сам T0 , T1 , S , M , L .:
f2	T0 , т.к. f2 0,0 1; f2	T1 , т.к. f2 1,1 1;
f2	S1 , т.к. на противоположных наборах (000) и (111)

функция принимает одинаковое значение, равное 1.

<<< < Предыдущая 1 2 3 4 5 6 7 8 910 / 1410 11 12 13 14 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
01.05.2022379.59 Кб1Учебное пособие 80051.pdf
#
01.05.20223.86 Mб6Учебное пособие 800510.pdf
#
01.05.20223.88 Mб4Учебное пособие 800511.pdf
#
01.05.20223.88 Mб20Учебное пособие 800512.pdf
#
01.05.20223.94 Mб4Учебное пособие 800513.pdf
#
01.05.20223.99 Mб6Учебное пособие 800514.pdf
#
01.05.20224 Mб6Учебное пособие 800515.pdf
#
01.05.20224 Mб5Учебное пособие 800516.pdf
#
01.05.20224.01 Mб9Учебное пособие 800517.pdf
#
01.05.20224.07 Mб15Учебное пособие 800518.pdf
#
01.05.20224.14 Mб14Учебное пособие 800519.pdf

			1						2						3

															x
y		y		1	f		x	y		z	xy	f 2	x	y	x	f

0	1			1	0	0		0		0	0	1
0	1			1	0	0		0		0	0	1	0	0	0	1

						0		0		1	0	1

													0	1	1	0

						0		1		0	0	1

													1	0	1	0

						0		1		1	0	1

													1	1	1	0

						1		0		0	0	1
						1		0		0	0	1

						1		0		1	0	1

						1		1		0	1	0

						1		1		1	1	1

			1						2						3

															x
y		y		1	f		x	y		z	xy	f 2	x	y	x	f

0	1			1	0	0		0		0	0	1
0	1			1	0	0		0		0	0	1	0	0	0	1

						0		0		1	0	1

													0	1	1	0

						0		1		0	0	1

													1	0	1	0

						0		1		1	0	1

													1	1	1	0

						1		0		0	0	1
						1		0		0	0	1

						1		0		1	0	1

						1		1		0	1	0

						1		1		1	1	1

			1						2						3

															x
y		y		1	f		x	y		z	xy	f 2	x	y	x	f

0	1			1	0	0		0		0	0	1
0	1			1	0	0		0		0	0	1	0	0	0	1

						0		0		1	0	1

													0	1	1	0

						0		1		0	0	1

													1	0	1	0

						0		1		1	0	1

													1	1	1	0

						1		0		0	0	1
						1		0		0	0	1

						1		0		1	0	1

						1		1		0	1	0

						1		1		1	1	1