
Учебное пособие 800182
.pdf
закона распределения (рис. 24) чаще всего встречаются значения X m1(x). Для точного определения одномерной плотности случайного сигнала необходимо исследовать реализацию бесконечной длительности. На практике же всегда имеют дело с реализациями конечной длительности. T0 и при изучении выборки берут всегда с точным шагом T. Соответственно число отсчетов случайного сигнала N=T0/T, подвергаемых обработке, всегда конечно. Поэтому вместо плотности вероятности p(x) получают ее оценку в виде гистограммы (рис. 25).
Рис. 23. Равномерный закон распределения
Рис. 24. Плотность вероятности
 P
P
P |
X |
k |
0 |
X |
min |
X |
|
|
max |
Рис. 25. Гистограмма плотности вероятности
С одномерной плотностью p(x) однозначно связана совокупность величин, являющихся параметрами случайного процесса и называемых моментами. Наибольшее распространение при описании случайных сигналов имеют математическое ожидание (начальный момент первого порядка) m1(x), дисперсия (центральный момент второго порядка) m2(x)=D(x) и связанная с дисперсией величина - среднеквадратическое отклонение. Если реализация случайного процесса задана в
39
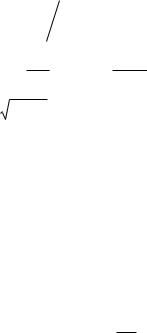
виде выборочной последовательности значений X1, i=1, 2, … N, то называемые параметры случайного процесса могут быть определены с помощью выражений:
|
|
N |
|
|
|
1 |
x |
|
i |
|
|
m |
|
X |
N , |
||
|
i 1 |
|
|
|
|
m |
x D x |
2 |
|
|
|
2 x
x
|
N |
X |
2 |
|
|
|
|
|
|
|
i |
|
|
|
|
i 1 |
N |
||
|
m |
x |
|
|
2 |
|
|
m |
|
N |
, |
x |
|
||
2 |
|
|
|
1 |
N 1 |
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
Поскольку случайные сигналы в радиотехнике представляют собой случайно изменяющиеся во времени напряжение или ток, математическое ожидание можно рассматривать как постоянную составляющую в спектре случайного сигнала, дисперсию – как среднюю мощность флуктуационной (переменной) составляющей, а среднеквадратическое отклонение – как среднюю амплитуду флуктуаций.
Энергетический спектр случайного сигнала Wx() показывает, как средняя мощность сигнала распределена по диапа-
зону частот. Это следует из выражения
m |
x |
1 |
|
||
2 |
|
2 |
|
|
|
d |
Wx |
|
|
|
.
Например, по графику энергетического спектра широкополосного случайного процесса (рис. 26) видно, что основная часть мощности сигнала приходится на область низких частот, прилегающих к =0. В то же время у узкополосного случайного сигнала (рис. 27) она сосредоточена вблизи частоты 0.
40
Рис. 26. Ширина спектра широкополосного случайного сигнала
Рис. 27. Ширина спектра узкополосного случайного сигнала
Для большинства случайных сигналов ширина спектра теоретически бесконечно велика. Для оценки реальной ширины спектра вводят понятие эффективной ширины энергетического спектра (энергетической ширины) wэ, которую можно определить, например, как полосу часто т, в пределах которой спектральная плотность средней мощности падает не более, чем в 2 раза по сравнению с максимумом (рис. 28, 29).
Корреляционная функция случайного процесса Rx( ) является мерой внутренней связности процесса в различные моменты времени, отстоящие на .
41

Рис. 28. Спектральная плотность
Рис. 29. Спектральная плотность
По корреляционной функции широкополосного процесса (рис. 29) видно, что с ростом временного сдвига связь между значениями X(t) и X(t+ ) постепенно уменьшается. Интервал корреляции (величина временного сдвига, начиная с которого значения сигнала X(t) и X(t+ ) могут считаться несвязанными) здесь относительно велик. Корреляционная функция узкополосного сигнала (рис. 29) имеет характерный вид затухающего гармонического колебания. Частая смена знака функции Rx() говорит о малой величине интервала корреляции в данном случае.
Оценку величины интервала корреляции процесса к при известной корреляционной функции Rx() можно провести следующим образом: если процесс широкополосный (рис. 27), то Rx() можно взять равным координате первого нуля функции Rx(): если процесс узкополосный (рис. 28), то определяют
42

по первому нулю огибающей функции Rx(). Если огибающая Rx( ) – монотонная, то определяют как время, за которое огибающая уменьшается в e раз.
Корреляционная функция Rx() и энергетический спектр процесса Wx() связаны между собой преобразованиями Фурье:
|
|
|
|
|
|
|
|
Wx Rx e |
j |
d , |
|||||
|
|
||||||
|
|
|
|
|
|
||
Rx |
1 |
|
|
|
|
|
|
Wx e |
j |
d. |
|||||
|
|||||||
2 |
|
|
|||||
|
|
|
|
|
|
||
|
|
|
|
|
|
||
Связаны между собой также интервал корреляции процесса и эффективная ширина его энергетического спектра.
э=const.
Поэтому при уменьшении эффективной ширины спектра интервал корреляции процесса увеличивается, и наоборот.
Если, как предполагалось и ранее, реализация случайного сигнала задана выборочной последовательностью значений Xi, то вначале можно определить корреляционную функцию
|
kT |
1 |
|
N k |
X |
|
m x X |
|
m x , |
||||||
R |
|
|
|
|
|||||||||||
|
|
i |
i k |
||||||||||||
x |
|
|
N k |
|
|
|
1 |
|
|
1 |
|||||
|
|
|
i |
1 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
0 k N1, |
|
|
|
|
|||||
|
|
|
|
N k |
|
|
|
|
|
|
k |
|
|
|
|
W |
n T |
|
R |
kT 1 |
|
|
cos kn , |
||||||||
|
|||||||||||||||
|
x |
|
|
|
x |
|
|
|
|
N1 |
|
|
|
||
|
|
|
|
i 1 |
|
|
|
|
|
|
|
|
|
||
0 k N,
где N1 – число отсчетов корреляционной функции и энергетического спектра, выбираемое примерно на 1 2 порядка меньшим числа отсчетов сигнала N, – шаг отсчетов по частоте.
43
1.Правила построения гистограмм
Исследуемый сигнал X(t) задан выборочной последовательностью значений Xi, i=1, 2, … N. Для построения гистограммы вначале находят минимальное Xmin и максимальное Xmax из Xi. Далее диапазон изменения переменной X (Xmin - Xmax) разбивают на отдельные интервалы, как правило, одинаковой ширины X. Число интервалов Nи берут равным 10 – 20. Соответственно
X = (Xmin - Xmax) / Nи,
а границы интервалов составляют:
для первого – Xmin X < Xmin + X,
для второго – Xmin + X X < Xmin + 2X, …
Анализируя выборочную последовательность Xi, определяют, сколько n1 значений попало в первый интервал, n2 – во второй и т.д. Если в какой-либо интервал попало слишком мало значений (n<<10), то данный интервал объединяют с одним из соседних. При этом ширина нового интервала Xi будет отличаться от остальных. В подобной ситуации можно объединять и несколько соседних интервалов.
При построении гистограммы (см. рис. 25) каждый столбец должен иметь ширину, пропорциональную ширине данного интервала, и высоту, пропорциональную Pk=nk/(NXk) – усредненной по ширине k-го интервала плотности вероятности пребывания сигнала X в k-ом интервале. Если все интервалы имеют одинаковую ширину, то для упрощения расчетов можно изменить масштаб по оси ординат и строить столбцы высотой пропорционально относительному числу значений (nk/N) в k-ом интервале или даже просто пропорционально nk.
2. Проверка на согласованность теоретического и статистического распределения по критерию 2 Пирсона
При выполнении лабораторной работы информацию о законе распределения исследуемого случайного сигнала получаем в виде гистограммы (статистического распределения).
44

Вид кривой, которую выдает машина, дает возможность предположить, что мгновенные значения случайного сигнала распределены по равномерному закону
|
1 |
, |
a x b, |
|
|
||
P x b |
a |
|
|
|
|
|
x a, x > b. |
0, |
|
|
|
|
|
|
|
Необходимо проверить, насколько велика вероятность справедливости этой гипотезы. Эту проверку можно осуществить по критерию 2 Пирсона. Процедура проверки такова:
1. Определяем теоретические вероятности P пребывания случайного сигнала в пределах каждого из интервалов X, соответствующих отдельным столбцам гистограммы. Поскольку число интервалов Ni=10, ширина всех интервалов одинакова, т.е.
X |
|
|
X |
max |
X |
min |
, |
|
|
|
|||||
|
|
|
|
|
|
||
|
k |
|
|
|
10 |
|
|
|
|
|
|
|
|
|
k=1, 2, …, 10,
то Pk = 0, 1, k=1, 2, … 10.
2. Используя известные параметры статистического распределения (гистограммы): nk –число отсчетов сигнала, попавших к k-ый интервал; N=400 – общее число исследуемых отсчетов; Nи – число столбцов гистограммы (Nи=10) и результаты расчетов по предыдущему пункту (Pk), определяем меру расхождения теоретического и статистического распределений
Nи |
nk |
2 |
|
2 |
NPk |
. |
|
|
|
||
k 1 |
|
NPk |
|
3. Определяем вероятность P согласованности теоретического и статистического распределений. При этом используем найденное ранее значение 2 и число степеней свободы
45
распределения, равна разности числа столбцов гистограмм (10) и числа наложенных условий. Оно равно трем: условие нормировки P=1, условие совпадения у теоретического и статистического распределений математического ожидания m1(x) и дисперсии D(x). В итоге z=10-3=7. Вероятность P определяем по табл. 3 [3]. Гипотезу о согласованности теоретического и статистического распределений отвергают, если P<<1.
Таблица 3
Таблица определения вероятностей
P |
2 |
P |
2 |
0,99 |
1,239 |
0,7 |
4,57 |
0,98 |
1,564 |
0,5 |
6,35 |
0,95 |
2,17 |
0,3 |
8,38 |
0,9 |
2,83 |
0,1 |
12,02 |
0,8 |
3,82 |
0,01 |
18,48 |
Задание и вопросы для лабораторной работы
Изучить теорию вопросов, рассматриваемых в данной лабораторной работе, по рекомендуемой литературе.
Внимательно изучить правила:
-построения гистограммы;
-определения согласованности теоретического и статистического распределений по критерию Пирсона;
-оценки интервала корреляции и эффективной ширины энергетического спектра сигнала.
1. Провести генерацию исходного случайного сигнала с заданными математическим ожиданием m(x) и среднеквадра-
тическим отклонением . Конкретный вариант задания указывает преподаватель. Возможные варианты задания приведены в табл. 4.
46
|
|
|
|
|
|
|
|
|
Таблица 4 |
||
|
|
|
Варианты заданий |
|
|
|
|
||||
|
|
|
|
|
Параметры |
|
|
|
|
||
Вари- |
Исходн. |
|
ФНЧ |
ПФ |
|
РФ |
|
||||
сигнал |
|
|
|
||||||||
ант |
|
|
|
|
|
|
|
|
|
||
m1(x) |
(x) |
|
f0 |
Q |
f0 |
|
Q |
f0 |
|
Q |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
1 |
|
1 |
0,707 |
3,5 |
|
5 |
3,5 |
|
3 |
2 |
1 |
2 |
|
1,5 |
0,707 |
3 |
|
5 |
3 |
|
2 |
3 |
0 |
1 |
|
2 |
0,707 |
4 |
|
5 |
4 |
|
2 |
4 |
-1 |
1 |
|
2,5 |
0,707 |
1 |
|
5 |
1 |
|
3 |
5 |
-1 |
2 |
|
3 |
0,707 |
1,5 |
|
5 |
1,5 |
|
3 |
6 |
0 |
2 |
|
3,5 |
0,707 |
2 |
|
5 |
2 |
|
3 |
2. Просмотреть на экране монитора и распечатать затем на принтере графики временной функции сигнала x(t), корреляционной функции Rx() и энергетического спектра Wx(f), гистограммы распределения мгновенных значений.
Примечание: на графиках x(t), Rx() масштаб по оси абсцисс – в секундах, на графике Wx(f) – в герцах, на гистограмме – в единицах переменной X, т.е. в вольтах. Определить оценки математического ожидания m1(x) и среднеквадратического отклонения исследуемого отрезка реализации.
3. По графикам корреляционной функции Rx() и энергетического спектра Wx(f) определить соответственно оценки интервала корреляции процесса X и энергетической ширины
спектра fx.
Примечание: для практически равномерной функции Wx(f) считать fx равной высшей частоте указанной на графике Wx(f). Найти произведение x fx.
4. По гистограмме определить вероятности P согласованности статистического (гистограммы) и теоретического распределений для равномерного варианта зависимости P(x). Оценку P проводить по критерию согласования 2 Пирсона.
47
5.Дать общую характеристику исходного случайного сигнала: процесс широкополосный или узкополосный; закон распределения близок к равномерному, нормальному, экспоненциальному и т.д.; процесс центрированный или нет.
6.Выполнить фильтрацию исходного случайного сигнала фильтрами с указанными параметрами (определяет преподаватель). Провести исследования пунктов 2, 3, 5 для откликов фильтров.
7.Сравнить временные диаграммы, а также характеристики исходного процесса x(t0) и трех вариантов отклика Y1(t), Y2(t), Y3(t). Объяснить явные изменения характеристик при соответствующих видах фильтрации. Проверить, выполняется ли
условие постоянства произведения f. Оценить качественно, произошла ли нормализация исходного процесса для каждого вида фильтрации. Сделать соответствующие выводы.
Содержание от чета
1.Распечатки временных зависимостей реализаций, гистограмм, графиков корреляционных функций и энергетических спектров.
2.Результаты оценки эффективной ширины энергетического спектра, интервала корреляции.
3.Выводы по соответствующим пунктам задания.
Контрольные вопросы
1.Назовите основные параметры случайного процесса. Каков их физический смысл?
2.Что такое корреляционная функция? Какую информацию о случайном сигнале она несет?
3.Что такое энергетический спектр случайного процесса? Почему для случайных процессов именно он является характеристикой в спектральной области?
4.Что такое эффективная ширина спектра? Что такое интервал корреляции? Как они связаны?
48
