Описание расчетной схемы

На первом этапе изучения конструктивно-нелинейных колебаний динамических систем рассмотрим следующую упрощенную расчетную схему. Она представляет собой недеформируемый стержень со свободными концами длиной 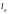, который опирается на две упругие связи с жесткостью в общем случае и . Будем считать изгибные деформации малыми. Плавность приложения нагрузки обеспечивается двумя переходными частями длиной и , которые служат только для передачи нагрузки на балку, когда сила находится на переходных частях. Их массой и собственной изгибной жесткостью мы пренебрегаем. Под концами стержня находятся ограничительные жесткие опоры. 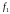Между концами стержня и жесткими опорами имеются вертикальные зазоры и . При движении по стержню нагрузки вертикальные зазоры изменяются и могут замкнуться и далее разомкнуться, т.е. концы стержня могут поочередно или одновременно опереться на жесткие опоры или оторваться от них (рис. 2). Предполагается, что по балке движется с постоянной скоростью сила, изменяющаяся по гармоническому закону: .

Рис. 2. Динамическая расчетная схема колебательной системы

Система дифференциальных уравнений относительно переменных и , полученная с использованием принципа возможных перемещений, описывает колебания балки без учета возможного опирания на ограничительные опоры и имеет вид

(1)

где 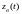– вертикальные перемещения центра тяжести стержня; – угол поворота стержня относительно центра тяжести; M – масса стержня; – момент инерции стержня

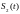
относительно центра тяжести; S_i(t) – усилие в i-й упругой связи; l_i – плечо i-й связи относительно середины стержня; – нагрузка, движущаяся по стержню со скоростью ; и усилия в вертикальных упругих связях, которые определяются через перемещения сечений стержня над упругими связями; – расстояние от начала стержня до левой упругой связи, – аналогично.

Координаты упругих связей определяются следующим образом:

; (2)

Перемещения точек прикрепления упругих связей (равны их деформациям) и возникающие в них усилия вычисляются по следующим формулам:

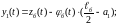
(3)

; (4)

Силы и передают действие силы 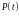на начало и конец стержня при ее движении по левой и правой переходным частям и соответственно вычисляются по формулам

; . (5)

Два подхода моделирования колебательного процесса с ограничительными опорами

Для выполнения численных исследований использованы два подхода моделирования конструктивной нелинейности:

В первом подходе колебательный процесс делится на временные интервалы, в пределах которых система уравнений движения остаётся неизменной. Так, например, когда оба зазора разомкнуты, решается система уравнений (1). При замыкании левого зазора изменяется расчетная схема колебательной системы и движение стержня описывает только уравнение угловых колебаний

, (6)

где и - угол поворота и момент инерции стержня относительно точки опирания на левую жесткую опору.

При замыкании зазора в конце стержня уравнение (6) принимает вид

(7)

где координаты и , определяющие движущейся силы и упругих связей, будут отсчитываться от точки опирания на правую опору в обратную сторону.

Полное вертикальное перемещение произвольного сечения стержня вычисляется по формуле

, (8)

где - расстояние до сечения от правой опоры.

В случае размыкания зазора происходит возвращение к первоначальной системе уравнений (1) и т.д. В общем случае количество интервалов может быть очень большим, что связано с упругими свойствами ограничительных опор. Чтобы избежать громоздких вычислений, считалось, что при замыкании зазора, энергия удара поглощается ограничительными опорами. Построен алгоритм и создана на его основе вычислительная программа, которая в автоматическом режиме определяет границы интервалов и решает необходимые уравнения.

Во втором подходе ограничительные опоры моделируются упругими или упруго-вязкими связями. Они включаются в работу колебательной системы, когда перемещения концов стержня становятся равными величине зазора f в момент касания. При этом используется система уравнений

(9)

где и усилия, возникающие в ограничительных опорах, с учетом вязкого сопротивления:

; (8)

Перемещения начала и конца стержня определяются через обобщенные координаты и :

(9)

где – коэффициент вязкого сопротивления.