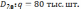Практические задания
Найти период заказа на склад материала при следующих условиях поставок (табл. 4).
Таблица 4
Вариант |
Количество выдачи |
Период выдачи |
Единовременная выплата |
Стоимость хранения |
1 |
40 |
15 |
200 |
0.4 |
2 |
60 |
7 |
150 |
0.25 |
3 |
50 |
7 |
40 |
0.1 |
4 |
60 |
12 |
40 |
0.23 |
5 |
60 |
10 |
60 |
0.4 |
6 |
20 |
7 |
120 |
0.2 |
7 |
53 |
17 |
145 |
0.3 |
8 |
70 |
9 |
50 |
0.16 |
9 |
63 |
8 |
48 |
0.4 |
10 |
75 |
12 |
76 |
0.45 |
11 |
53 |
6 |
300 |
0.22 |
12 |
48 |
9 |
200 |
0.34 |
13 |
43 |
5 |
50 |
0.3 |
14 |
50 |
5 |
90 |
0.29 |
15 |
60 |
7 |
130 |
0.32 |
Контрольные вопросы
1. Из чего складывается стоимость всех затрат?
2. Как найти затраты на хранение?
З. Как найти величину n?
4. Как, зная величину n, найти общие затраты?
ЛАБОРАТОРНАЯ РАБОТА № 6
МОДЕЛИРОВАНИЕ УПРАВЛЕНИЯ ЗАПАСАМИ С УЧЕТОМ ШТРАФОВ ЗА НЕВОЗМОЖНОСТЬ ПОСТАВОК
Цель работы: получение навыков в моделировании и анализе моделей, применяемых в управлении запасами машиностроительного производства.
Теоретические основы
Пусть известно, что поставки какого-либо материала должны осуществляться в течение п временных периодов при условии, что известны значения D, i=1, …, n каждой из них. Величина с определяет прибыль от поставки каждой единицы материала, g - штраф за каждую не поставленную единицу материала, h- стоимость хранения избытка материала. При условии ограниченности складских помещений, необходимо найти величину q постоянного заказа материала в каждый период времени.
Пронумеруем
величины опросов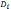 
так, чтобы они стояли по возрастанию:
.
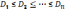Тогда партия заказа будет находится
между какими-то номерами k
и k+1:
.
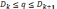Запишем функцию прибыли от поставок материала за n периодов:
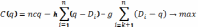
Задача заключается в нахождении такого номера к и величины q, чтобы функция имела максимальное значение.
Данная задача решается с применением теории двойственности в задачах линейного программирования. Опишем алгоритм поиска оптимальной партии заказа q:
1. Упорядочить все D, по возрастанию.
2.
Вычислить величину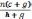 
.
3.
Найти номер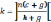 
,
где знак 
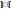означает, что если k
получается целым числом, то оно и берется,
а если k
дробное, то берется его целая часть +1.
4.
q
берется равным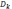 
.
Пример
Найти оптимальную партию заказа заготовок при условии, что количество периодов спроса равно 20 неделям, прибыль от продажи одной тыс. шт. равна 4 руб., затраты на хранение одной тыс. шт. равны 3 руб., штраф за недопоставку одной тыс. шт. равен 5 руб. Данные о спросе находятся в таблице 5.
Таблица 5
Номер недели |
Спрос (тыс. шт.) |
Номер недели |
Спрос (тыс. шт.) |
1 |
10 |
11 |
50 |
2 |
90 |
12 |
60 |
3 |
20 |
13 |
23 |
4 |
16 |
14 |
72 |
5 |
15 |
15 |
13 |
6 |
45 |
16 |
56 |
7 |
100 |
17 |
34 |
8 |
12 |
18 |
54 |
9 |
78 |
19 |
25 |
10 |
34 |
20 |
80 |
Упорядочим величины спроса по возрастанию:
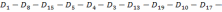
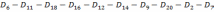
Найдем номер k=20x(4+3)/(5+3)=18 (с учетом округления).
Под 18 номером в списке по возрастанию стоит
