Примеры

Пример 1. Распределение работ.

Фирма получила заказы на разработку пяти программных продуктов. Для выполнения этих заказов решено привлечь пятерых наиболее опытных программистов. Каждый из них должен написать одну программу. В следующей таблице приведены оценки времени (в днях), необходимого программистам для выполнения каждой из этих работ:

Оценки даны самими программистами, и у фирмы нет основания им не доверять.

Распределите работы между программистами, чтобы общее количество человекодней, затраченное на выполнение всех пяти заказов, было минимальным.

Вопросы:

1. Какое минимальное количество человекодней необходимо для выполнения всех пяти заказов?

2. Какую программу следует поручить Малкину?

3. Какую программу следует поручить Залкинду?

Решение. Таблица задачи о назначениях представлена в условии. Проведя расчеты, получаем следующую матрицу назначений:

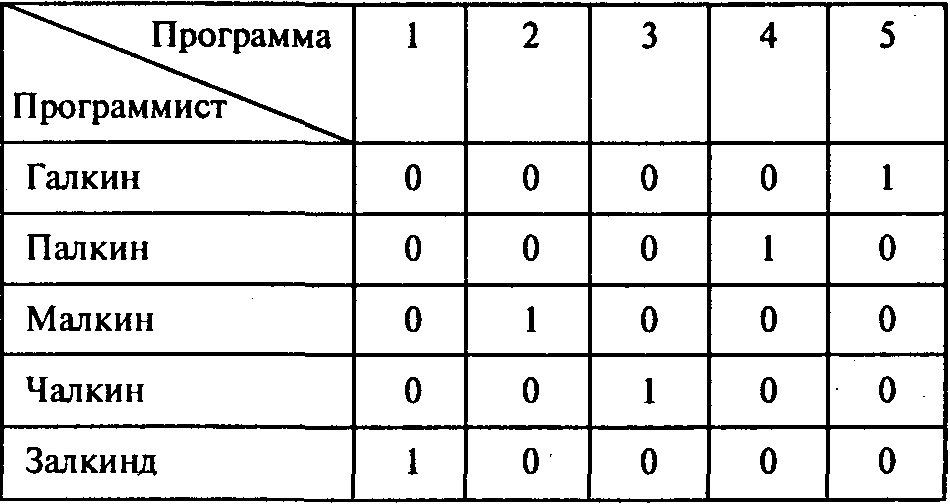
Учитывая исходную информацию, получаем следующий результат:

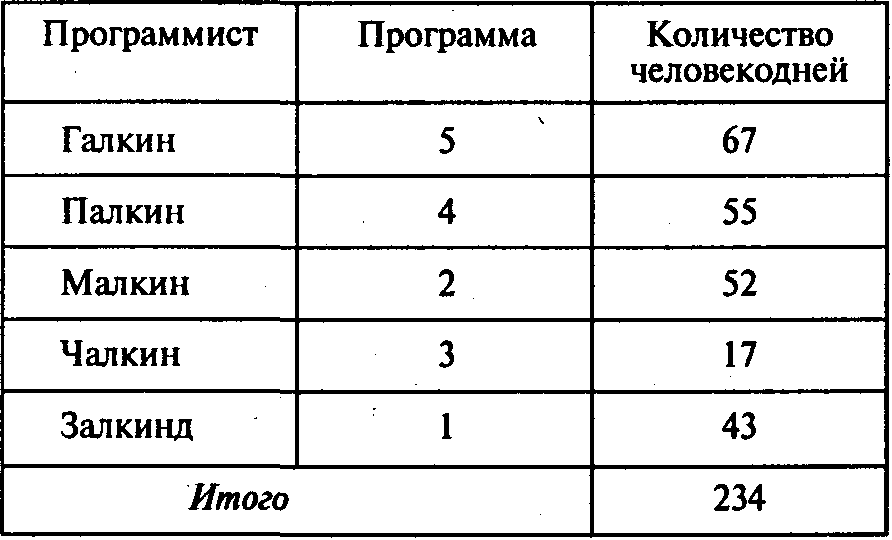
Ответы: 1. 234 человекодня. 2. Программу 2. 3. Программу 1.

Вопросы

Вопрос 1. Задача о назначениях относится к классу задач:

1) линейного программирования;

2) эконометрических;

3) статистических;

4) имитационных;

5) не относится ни к одному из указанных классов.

Вопрос 2. Имеются две работы r₁, r₂, и два рабочих L₁ , L₂, каждый из которых может выполнить любую работу. Элемент a_ij матрицы А показывает время, необходимое рабочему i для выполнения работы j:

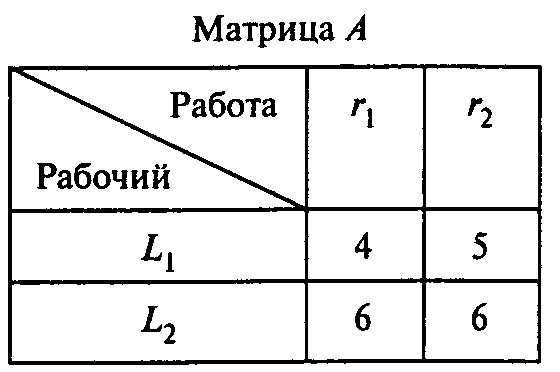
Решите задачу о назначениях. Чему равно минимальное время выполнения двух работ?

Варианты ответов:

1) 9; 2) 10; 3) 11; 4) 12; 5)13.

Вопрос 3. Как известно, задача о назначениях является частным случаем транспортной задачи. Какая из приведенных ниже характеристик транспортной таблицы, построенной для задачи о назначениях, наиболее правильная?

Варианты ответов:

1) объемы потребления равны единице, объемы поставок отличны от единицы;

2) объемы поставок равны единице, объемы потребления отличны от единицы;

3) матрица транспортных затрат квадратная, объемы поставок отличны от единицы;

4) матрица транспортных затрат квадратная, объемы потребления отличны от единицы;

5) матрица транспортных затрат прямоугольная, объемы поставок равны единице.

Вопрос 4. Оптимальный план задачи о назначениях можно представить в виде:

1) квадратной матрицы, в каждой строке которой находится одна единица;

2) квадратной матрицы, в каждом столбце которой находится одна единица;

3) квадратной матрицы, в каждой строке и в каждом столбце которой находится одна единица;

4) квадратной матрицы, в каждой строке которой находится хотя бы одна единица;

5) квадратной матрицы, в каждом столбце которой находится хотя бы одна единица.

Вопрос 5. Имеются две работы r₁, r₂ и трое рабочих L₁, L₂ и L₃, каждый из которых может выполнить любую работу. Элемент а_ij матрицы А показывает время, необходимое рабочему i для выполнения работы j:

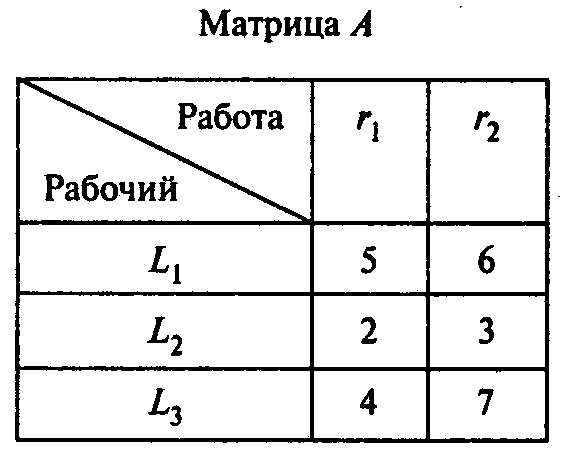
Решите задачу о назначениях. Чему равно минимальное время выполнения двух работ?

Варианты ответов:

1) 5; 2) 6; 3) 7; 4) 8; 5) 9.

Задачи

Задача 1. Цех металлообработки получил срочный заказ на выпуск партии деталей. Для производства детали необходимо выполнить операции на четырех станках. В цехе работают четыре слесаря высокой квалификации, каждый из которых может работать на любом станке, но с различным процентом брака (процент брака известен из документации ОТК):

Распределите станки между рабочими таким образом, чтобы процент брака был минимальным. (Предполагается, что ОТК проверяет готовую деталь, т.е. общий процент брака определяется как сумма процентов брака, допущенного всеми рабочими.)

Вопросы:

1. На каком станке должен работать рабочий 2?

2. Чему равен минимальный общий процент брака?

Задача 2. Самолеты компании «Аэрофлот» летают между Москвой и Сочи. Полеты беспосадочные. График движения показан в следующей таблице:

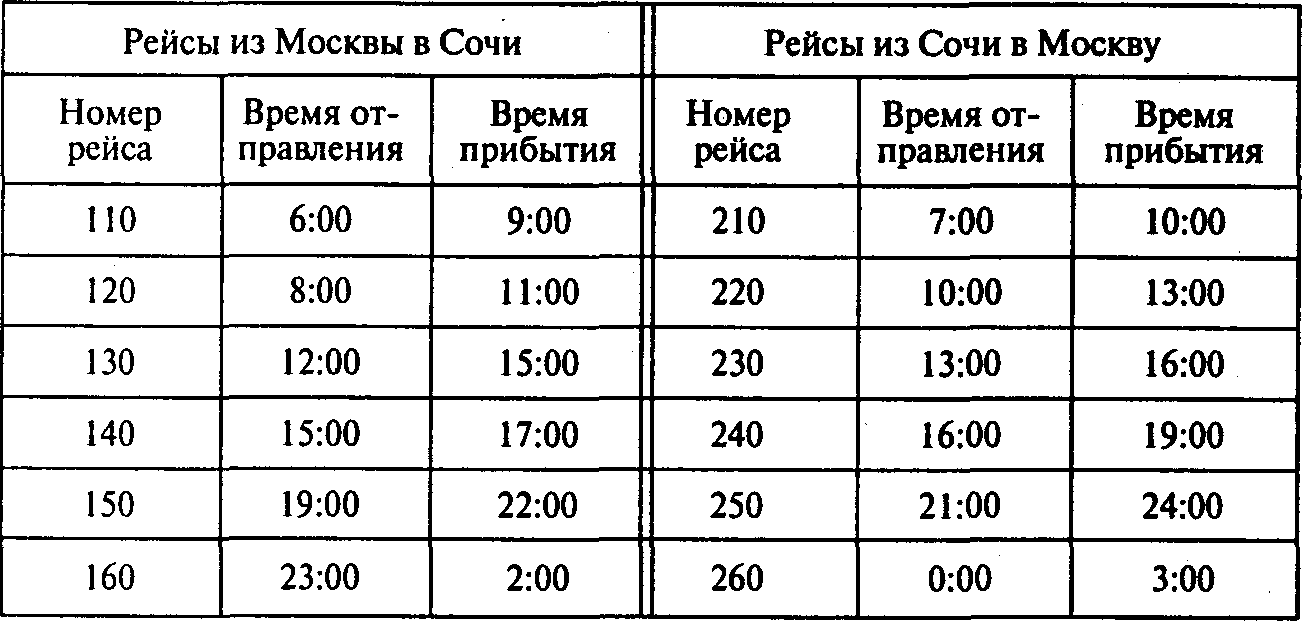
Рейсы могут обслуживаться московскими или сочинскими экипажами. Любой экипаж выполняет пару рейсов — «туда и обратно». Время, необходимое для подготовки самолета к очередному рейсу, — один час. Требуется определить, какую пару рейсов следует выполнять каждому экипажу и из какого отряда, московского или сочинского, должен быть соответствующий экипаж. Распределение рейсов необходимо осуществить таким образом, чтобы суммарное время ожидания вылета в «чужом» городе было минимальным. Время ожидания не включает тот час, который уходит на подготовку самолета к очередному рейсу.

Вопросы:

1. Верно ли, что рейс 210 должен выполняться московским экипажем?

2. Верно ли, что рейсы 240 и 160 должны выполняться одним экипажем?

3. Верно ли, что рейс 160 должен обслуживаться сочинским экипажем?

4. Каково минимальное общее время пребывания экипажей в «чужих» городах?

5. Какое количество рейсов должны выполнять московские экипажи?

ЗАДАНИЕ 5. ИМИТАЦИОННОЕ МОДЕЛИРОВАНИЕ

Цели

Имитация — это попытка дублировать особенности, внешний вид и характеристики реальной системы. Идея имитации реализуется следующим образом:

1) математическое описание реальной ситуации;

2) изучение ее свойств и особенностей;

3) формирование выводов и принятие решений, связанных с воздействием на эту ситуацию и основанных на результатах имитации.

Важно, что реальная система не подвергается воздействию до тех пор, пока преимущества или недостатки тех или иных управленческих решений не будут оценены с помощью модели этой системы.

Модели

Метод Монте-Карло (метод статистических испытаний) состоит из четырех этапов:

1) построение математической модели системы, описывающей зависимость моделируемых характеристик от значений стохастических переменных;

2) установление распределения вероятностей для стохастических переменных;

3) установление интервала случайных чисел для каждой стохастической переменной и генерация случайных чисел;

4) имитация поведения системы путем проведения многих испытаний и получение оценки моделируемой характеристики системы при фиксированных значениях параметров управления. Оценка точности результата.

Существует два подхода в имитационном моделировании динамических процессов.

Первый заключается в том, что весь период моделирования разбивается на равные промежутки времени (такты моделирования) и анализ состояния системы, а также значений выходных переменных производится через одинаковые промежутки времени. При таком подходе возникает проблема выбора «правильной» продолжительности такта. Кроме того, не исключается появление тактов, в которых состояние системы по сравнению с предыдущим не изменилось.

При втором подходе величина такта моделирования не фиксируется, моделирование в этом случае происходит в момент наступления одного из «существенных» событий. Например, при моделировании производственного процесса на предприятии такими событиями могут быть освобождение или начало загрузки станка, поступление на обработку детали, невыход на работу станочника, исчерпание запаса необходимых комплектующих деталей на складе и др. Именно второй подход чаще всего используется на практике и поддерживается современными языками моделирования.

Широкое распространение получили два метода статистических испытаний. Один из них предполагает проведение достаточно большого числа Т последовательных наблюдений в течение одного прогона модели (одного сеанса имитирования).

Другой метод заключается в реализации т независимых прогонов модели, т.е. в m-кратном повторении одного и того же цикла имитирования. При этом, если мы хотим получить в сумме Т наблюдений, в течение каждого прогона можно делать по Т/т (допустим, что это число целое) наблюдений. Оба метода дают примерно одинаковый результат.

Пусть значения у_t (t = 1,..., Т) представляют собой результаты Т последовательных измерений значений случайной величины y во время одного и того же сеанса имитации. Среднее по времени значение у определяется выражением

Обозначим через  математическое ожидание случайной величины у. Тогда для достаточно большого T получаем

Оценка дисперсии (если временной ряд не является автокоррелированным) имеет вид

где D(у) — дисперсия случайной величины у.

Для оценки качества результатов, полученных методом Монте-Карло при неизвестной дисперсии наблюдаемой случайной величины, предположим, что Z — характеристика, которая должна быть определена (вероятность события, математическое ожидание, дисперсия и т.п.), a  — ее значение, уточняемое по мере накопления данных, остающееся случайным вследствие ограниченности числа T проведенных наблюдений. В этих условиях можно говорить о вероятности p(|Z – | < ) по отношению к интересующей нас характеристике. Величина |Z – | представляет собой погрешность в оценке Z, a  — некоторый допустимый ее предел.

Из неравенства Чебышёва следует

Из этого неравенства следует

откуда при заданных р и  и при известной зависимости D_ (Т) можно найти предельно необходимое Т.

Известно, что истинная дисперсия выборочного распределения для расчетного среднего обратно пропорциональна суммарному числу наблюдений Т, т.е.

где d не зависит от Т.

В начале имитационного процесса требуемое число наблюдений определить обычно не удается, поскольку d неизвестно. Поэтому, как правило, эксперимент проводят в два этапа.

На первом этапе число испытаний выбирается относительно небольшим, в результате определяется величина d. После этого можно уже определить, сколько дополнительных наблюдений необходимо, чтобы была достигнута требуемая точность.

Предельное число наблюдений Т₀ определяется формулой T₀ = d/[(1 – p)²].

При любом числе наблюдений больше Т₀ обеспечивается требуемая точность.