Разрешение математической модели процессов обмена в ожиженном слое с направленным движением фракций

Аналитическими методами исследованы процессы обмена, модели которых базируются на известных соотношениях баланса масс и теплоты. Построено приближенное решение системы модельных уравнений, описывающих кинетику температур и влагосодержаний дисперсного материала и теплоносителя. Приведены условия корректности используемого приближения

1. В настоящей работе в качестве модельных уравнений, описывающих процессы массо- и теплообмена между дисперсной и непрерывной подсистемами слоя во втором периоде сушки приняты соотношения работы [1]. Вместе с тем, в качестве дополнительных условий мы пренебрегаем теплообменом между стенкой сушильной камеры и псевдоожиженным слоем, а также – между стенкой аппарата и внешней средой. В отличие от работы [1], в которой уравнения модели решаются численными методами, в настоящей работе для разрешения модели применяются аналитические методы. Для уравнения массообмена, сформулированных в виде уравнений для теплоемкостей материала и теплоносителя, получены точные решения. Уравнения, описывающие теплообмен между подсистемами слоя, решаются методом возмущений [2] в предположении малости отношения коэффициента сушки к массовому расходу теплоносителя.

2. Из соотношений баланса масс по влаге для дисперсной и непрерывной фракций слоя вытекают следующие уравнения для теплоемкостей этих подсистем

(1)

где производная берется по безразмерной переменной 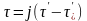, , - расход теплоносителя, 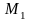и - массы материала и теплоносителя в псевдоожиженном слое, - текущее время, - время окончания периода с постоянной скоростью сушки

,

, , ,

,

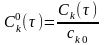(2)

, , , ,

где 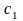, , , - удельные теплоемкости сухого материала, сухого газа, жидкости и пара;

, - текущие значения влагосодержаний материала и газа;

- равновесное влагосодержание материала;

, - расходы материала и теплоносителя;

- суммарная площадь поверхности частиц материала в слое;

- газосодержание слоя;

параметр - играет роль безразмерного коэффициента сушки.

Пренебрегая тепловым влиянием на слой границ сушильной камеры и газораспределительной решетки, из соотношений теплового баланса для материала и теплоносителя можно получить уравнения для температур дисперсной и газовой подсистем слоя в следующем виде

(3)

где

, , , , , (4)

, , , ,

, .

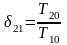Величины, введенные в (4), имеют следующий смысл: - температуры материала и теплоносителя в слое; - удельная теплота парообразования; - коэффициент теплообмена между газом и материалом. Смысл остальных величин виден из формул.

Таким образом, соотношения материального и теплового балансов для подсистем слоя совместно с принятыми упрощающими модель условиями приводят к начальным задачам для двух векторно-матричных дифференциальных уравнений, описывающих динамику изменения теплоемкостей и температур подсистем слоя.

3. Из уравнения и начального условия в (1) получим выражения для теплоемкостей подсистем слоя и для параметра 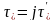, определяющего продолжительность периода поверхностного испарения влаги из частиц материала. Интегрируя уравнение (1) для случая различных собственных чисел матрицы , имеем

, (5)

Из выражений (5) видно, что в случае несовпадающих собственных числах матрицы , процесс приближения теплоемкостей и равновесным значениям определяется двумя временами релаксации

. (6)

Легко видеть, что в случае двукратного собственного числа, процесс массообмена характеризуется только одним релаксационным параметром .

При отыскании выражения для параметра воспользуемся методикой, изложенной в работах [3] и [4]. Воспользуемся с этой целью выражениями (5) и формулами для теплоемкостей, полученными из решения уравнения типа (1) для первого периода сушки. Приравняв значения теплоемкостей и производных при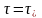 для первого и второго периодов, получим

(7)

(8)

где , - время окончания первого периода сушки в псевдоожиженном слое при ,

- влагосодержание материала в момент начала сушки,

,

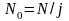- постоянная скорость сушки в первом периоде.

При значениях аргумента логарифмической функции в (7) близких к единице, приближенное выражение для продолжительности первого периода сушки имеет вид:

(9)

где и - продолжительности первого периода сушки в случаях слоя с направленным перемещением материала и без направленного перемещения материала, .

Если отношение массовых расходов материала и теплоносителя является малой величиной - , то выражение для времени окончания первого периода принимает вид:

(10)

В предельном случае из выражения (10) получаем формулу для псевдоожиженного слоя без направленного перемещения материала (8), совпадающую с аналогичной формулой работы [3].

4. Решение температурного уравнения (3) получим для случая 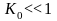, ограничившись главным членом разложения

(11)

.

Выполним разложения по этому параметру матриц и свободного члена в (3). Имеем:

(12)

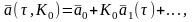
где -единичная матрица,

, , , ,

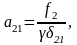
(13)

Подставляя в уравнение (3) разложения (11) и (12), получим следующее уравнение, определяющее первое приближение для температур подсистем слоя:

. (14)

Из (13) видно, что матрица имеет различные и отрицательные собственные числа при всех физически допустимых значениях параметров, где

, , .

Поэтому решение уравнения (14) имеет вид:

, (15)

где - собственные векторы матрицы ,

- частное решение уравнения (14),

, ,

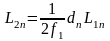, (16)

, .

В обозначениях (16) решение (15) принимает вид

, (17)

где

Выражение (17) описывает кинетику температур материала и теплоносителя при малых величинах безразмерного коэффициента сушки Подобное приближение использовалось, например, в работе [3] для получения оценочных сведений о теплообмене в псевдоожиженном слое без направленного перемещения материала. Отметим, что пренебрегая в решении членами порядка , фактически пренебрегаем влиянием изменения влагосодержанийматериала и газа на процесс теплообмена между этими подсистемами слоя.

Из формул для теплоемкостей (5) видно, что такое приближение является удовлетворительным при выполненном условии

Тепловая релаксация подсистем слоя, протекающая в два этапа, в этом приближении характеризуется следующими временными масштабами

(18)

В случае псевдоожиженного слоя с достаточно малым газосодержанием , выражения (18) принимает вид:

,

В этом случае коэффициенты в решении (15) являются рациональными функциями аргументов и :

(19)

где , ,

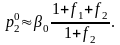
При больших значениях отношения поверхности материала к условной термодинамической поверхности , выражения для температур подсистем слоя слабо зависят от этого отношения и приближенно описываются формулами

где

Литература

1. Баумштейн И.П., Лыков А.В., Людмирский М.И., Майзель Ю.А. Исследование сушильных установок с помощью математического моделирования // Тепло- и массоперенос в процессе сушки и термообработки: сб. ст. – Минск: Наука и техника, 1970. - с.53-79.

2. Найфэ А. Введение в методы возмущений. М.: Мир, 1984. - 535 с.

3. Шишацкий Ю.И., Бырбыткин В.А., Лавров С.В. Математическое описание процесса сушки материалов в псевдоожиженном слое // Вестник ВГТУ. – 2006.- Т.2 - №6.- с.56-61.

4. Агапов Ю.Н., Бырдин А.П., Лукьяненко В.И., Стогней В.Г. Термокинетика динамического слоя в начальных стадиях тепловой релаксации // Вестник ВГТУ. – 2007.- Т.3 - №6.- с.27-32.

Воронежский государственный технический университет

УДК 621.91.01

Ю.А. Цеханов