3.4 Исследование взаимодействия компонентов социотехнических систем с использованием структурно-параметрической модели

Структурно-параметрическая модель применяется в основном для анализа технологических систем, либо систем с четко известными законами функционирования. Структурно-параметрическая модель позволяет исследовать качество взаимодействия компонентов сложных систем, его глубину, а также предлагает методы оптимизации взаимодействии.

С позиции данного подхода под системой понимается совокупность компонент (рисунке 3.4):

, где - множество входных параметров системы; - множество выходных параметров системы; F - закон функционирования системы - функционал, преобразующий набор входных параметров в набор выходных ; T - задержка системы, характеризующая инертность ее функционирования.

Причем такой фактор, как состояние системы, определяется наличием обратной связи, образованной соединением части ее выходов с частью ее входов. Пусть определена вещественная функция полезности системы Si с точки зрения ее цели .

Пусть также с некоторым числом входов S₁ соединено некоторое число выходов S₁. Необходимо определить характер влияния взаимодействия систем на полезность q₁.

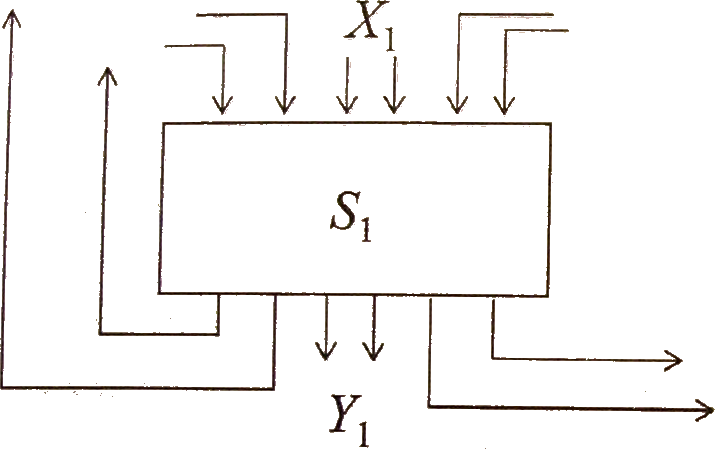
Рисунок 3.4 – Представление систем с позиции структурно-параметрической модели

Для этого следует найти производную функ­ции полезности по воздействию системы S₁

Если эта производная положительна, имеет место содействие систем в плане полезности q₁, если отрицательна - противодействие, если равна нулю - нейтралитет или независимость. Однако эти утверждения справедливы только для строгих видов взаимодействий [121].

Величина производной по модулю характеризует глубину строгого взаимодействия.

Допустим, что надсистема S включает некоторые подсистемы S_i и и имеет некоторую цель, в смысле которой ее функционирование обеспечивает полезность q(S) = q(S_i, S_j).

В общем случае предположим, что подсистемы зависимы, и соответствующие функции полезности приведены к безразмерным величинам (пронормированы), и их можно сравнивать через разность , где - общая полезность надсистемы при взаимодействии подсистем S_i и - общая полезность надсистемы, при функционировании в ее соста­ве только лишь подсистемы S_i.

Тогда характеризует приращение полезности надсистемы при начале функционирования в подсистемы S_j. Этот показатель может служить оценкой меры, характеризующей степень отношений в смысле достижения общей цели. Действительно, если , то системы симметрично независимы, если то имеет место противодействие. Причем значение характеризует так называемую глубину взаимодействия.

Такой показатель удобно использовать при оценке отношений эксплуатации. Получается, что система S_j эксплуатирует S_j в смысле полезности q_i если причем эксплуатация является доброжелательной, при , нормальной при , злобной при .

Интенсивность (остроту) взаимодействия можно измерить суммой . По мере убывания этой суммы возрастает интенсивность взаимного противодействия, по мере ее возрастания - интенсивность взаимного содействия.

Взаимодействие S_i и S_j следует рассмат­ривать по отношению к системным свойст­вам, представляя функцию полезности всей системы как функцию взаимовлияния двух переменных S_i и S_j. Именно здесь можно сравнивать величины и в зависимости от результатов этого сравнения классифицировать введенные отношения [126].

При наличии у всей системы нескольких целей общую полезность можно рассчитать как , где некоторый весовой коэффициент. Тогда общий характер взаимодействия подсистем можно рассчитать с учетом некоторой метрики в пространстве, образуемом величинами q_k

, (3.16)

например, определив расстояние в этом пространстве формулой .

Устранение противодействия связано с изменением окружения, формированием таких условий, структурных, функциональных, параметрических и других преобразований, а также выбор и построение различных схем компромисса, позволяющих обеспечить выполнение условия .

Теоретико-вероятностный подход. Для стохастических систем в качестве функции полезности рассмотрим вероятность достижения системой заданной цели. При этом можно говорить о конфликте случайных событий, заключающемся в достижении некоторых целевых состояний.

Пусть система А имеет вероятность реализации своей цели Р(А), тогда при введении в ее окружение системы В при реализации ею своей цели эта вероятность станет равна Р(А/В).

Если выполняется условие P(A/В) ~ Р(А) значит, между системами имеет место нейтралитет или независимость.

Если Р(А / В) < Р(А) имеет место противодействие.

Если Р(А / В) > Р(А) содействие.

Рассмотрим рефлексивную игру в предположении, что стороны действуют только исходя из текущей ситуации, игнорируя предысторию. Тогда можно применить марковскую модель процесса. Действие одной системы приводит к ответным изменениям свойств и последующему действию другой стороны. Будем полагать, что каждое действие приносит некоторый (частный) выигрыш; из частных выигрышей складывается результирующий выигрыш (проигрыш) - по завершении рефлексивной игры. В качестве количественной меры оценки состояний рефлексивной игры может быть использована плотность распределения вероятностей состояния частных и результирующего выигрышей, и построим линейную модель процесса [127].

Аналитически рефлексивная игра может быть описана на основе следующего общего соотношения для марковских процессов:

, (3.17)

где - плотность переходов в предыдущие состояния; - соответственно переходная вероятность и плотность вероятностей времени переходов из состояния i в j. Введя преобразование Лапласа, получим операторное выражение , где - преобразования Лапласа от функций соответственно; W_ij(s) - вероятностная передаточная функция из состояния i в j.

Модель справедлива и по отношению к - среднему количеству переходов в состояние i:

(3.18)

Для поглощающих состояний вероятность пребывания в нем равна среднему, если i - поглощающее со­стояние. Для остальных состояний

, (3.19)

где . Отсюда , где - среднее количество переходов в состояние к через i. В операторной форме .

Статистические характеристики Р_ij и w_ij (t) вычисляются на основании априорных данных.

Пусть конфликтуют две системы, А и В, состоящие из подсистем (компонентов), способных на самостоятельные действия и имеющих свои целевые функции. Исходной информацией являются статистические характеристики функционирования компонентов каждой системы на i-этапе конфликта в виде плотности распределения вероятностей времени достижения ими цели и статистические характеристики времени начала действия также в виде плотности распределения вероятностей времени начала действия (при условии, что действие происходит мгновенно) (рисунок 3.5).

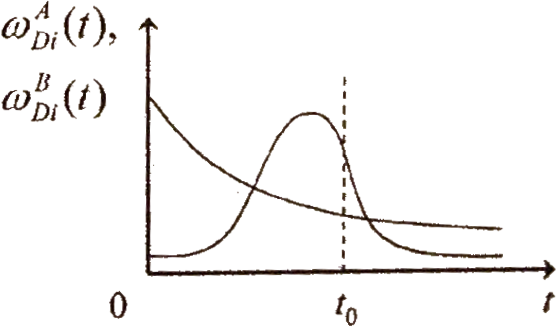
Рисунок 3.5 – Плотности вероятностей времени начала системами действия

Плотность распределения вероятностей успешного для системы А исхода на i-этапе (рисунок 3.6).

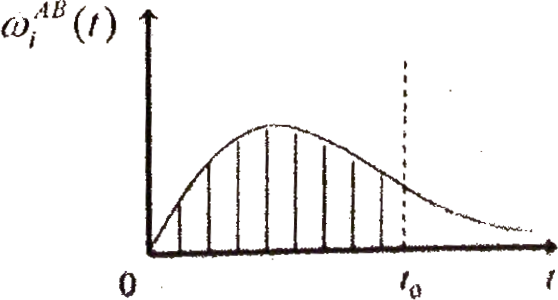
Рисунок 3.6 – Функция распределения вероятности факта выигрыша системы

Проинтегрировав эту функцию по времени, получим вероятность перехода системы А в успешное состояние на i - этапе рефлексивной игры ко времени t:

(3.20)

Плотность распределения вероятностей времен достижения цели компонентами системы А раньше, чем В осуществит ответное действие, равна . Для стороны В соответственно . Соответствующие формулы для действий сторон; , .

Применив преобразование Лапласа, получим операторную модель в передаточных функциях. При этом , .

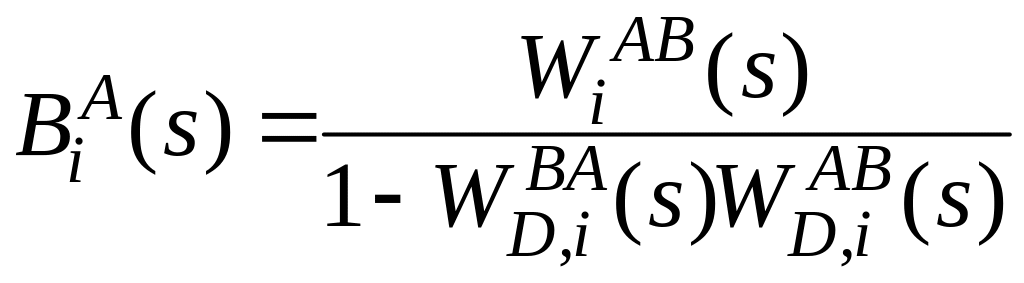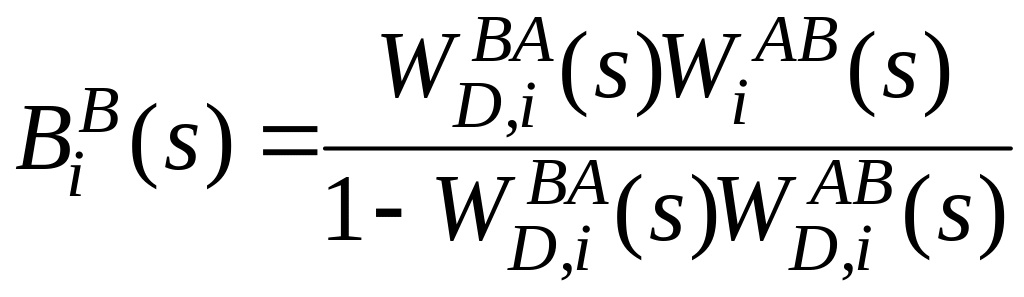На основе правил структурного преобразования передаточных функций модель может быть приведена к элементарному по структуре виду. Однако аналитическое выражение для результирующих передаточных функций, как правило, оказывается сложным и трудным для точного количественного анализа.

Энтропийный подход. Предположим, что системы А и В в процессе достижения своих целей взаимодействуют в некоторой среде S с общей целью.

Каждая из систем характеризуется сово­купностью возможных целевых состояний: заметим, что простое перечисление таких состояний системы А не характеризует полностью ее поведения, т.к. оно определяется не только необходимостью реализации конкретных состояний, но также и возможностями реализации этих состояний, определяемых средой функционирования S, в которую включена и система В со своими интересами [154].

Очевидно также, что степень реализации отдельных состояний системы А может описываться некоторой функцией полезности P(a_j), причем если состояние более жела­тельно, чем a_j, то P(a_j) > P(a_j).

Для стохастических систем естественно в качестве функции полезности рассматри­вать вероятности реализации состояний сис­темы А, т.е .

Поскольку система А взаимодействует с системой В, то необходимо анализировать возможности деятельности системы А с уче­том системы В, т.е. все возможные состоя­ния в предположении, что состоя­ния имеют место. Это в свою очередь означает анализ всех возмож­ных ситуаций. Для такого анализа необхо­димо отображение всего множества возмож­ных состояний систем А и В на числовое множество, обладающее свойством полного упорядочивания по Р. Другими словами, формально можно записать все множество возможных состояний для которых .

Тогда зависимость системы А от системы В означает наличие по крайней ме­ре одного состояния a_ij для которого найдет­ся по крайней мере одно состояние такое, что .