3.3 Построение теоретико-множественной модели рефлексивных игр социотехнических систем

Структурно-параметрическое моделирование применяется в основном для анализа технологических систем, либо систем с четко известными законами функционирования. Структурно-параметрическая модель позволяет исследовать качество взаимодействия компонентов сложных социотехнических систем, его глубину, а также предлагает методы оптимизации взаимодействий.

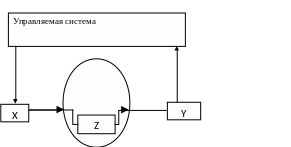
С позиции данного подхода под системой понимается совокупность компонент: S = X, Y, Z, F, τ где:

Х = {x_i}, - множество входных данных системы;

Z = {z_i}, - множество внутренних данных системы;

Y= {y_i}, - множество выходных данных системы;

F - закон функционирования системы - функционал, преобразующий набор входных параметров в набор выходных:

Y₁(t+ τ) = F₁(X₁(t)); (3.9)

τ - задержка системы, характеризующая инертность ее функционирования.

Рассмотрим активную фазу информационного конфликта (рисунок 3.5), когда одна из сторон S_T атакует другую S_Y. Объектами применения информационного оружия в данном случае являются уязвимость данных: X_T - входных и Z_T - внутренних (по отношению к оператору атаки Т). Соответственно, Х и Z - демилитаризованные (в отношении Т) подмножества данных. Выходные данные системы S_Y определяет ее оператор F из атакованных множеств данных и , как продукт атаки даны Т(Х)= _uT(Z)= . Теоретически возможна и атака оператора, когда T(F)= , .

Она сложнее в реализации, но и опаснее для S_Y. Довольно часто приходится иметь дело с комплексной атакой, когда .

Описание подобных процессов уместно осуществлять в пространстве нечетких переменных, где ущерб от атаки u определяется метрикой u=ρ[ ,Y], а риск R_isk(u) = u P(u), где P(u) - вероятность наступления ущерба величины u.

а)

б)

Рисунок 3.3 – Структура информационного управления социотехническими системами

Далее, рассматривая Х = Х + X_T и Z = Z + Z_T, обратимся к анализу многообразия информационных атак.

К примеру, атака уничтожения или D_l - атака предусматривает стирание D_l подмножества X_T

= Х + [D_l(X_T)] (3.10)

Одной из характеристик ущерба в данном случае может служить коэффициент полноты u = К_П = , где V - оператор определения объема информации в множествах данных. Если же наряду со стиранием D_l осуществляется также запись W_r некой сторонней информации Х^Т, то имеет место модификация или D_l /W_r - атака следующего содержания = X_T + [D_l(X_T)] + [W_r(X^T)], где ущерб можно оценить через коэффициент избыточности u = К_И = .

При Х = имеет место прямая подмена данных.

Атака несанкционированного доступа или R_d - атака состоит в чтении R_d подмножества уязвимых данных. Злоумышленники чаще стараются реализовать это в отношении внутренних данных Z, тогда ущерб характеризует коэффициент конфиденциальности u = К_К = , где С - функция полезности (ценности) данных.Отсюда кражу информации описывает модель = Z +[R_d(Z_T)] +[D_l(Z_T)].

Атаку на актуальность информации можно пояснить через параметр задержки τ входных данных =F[ (t - τ), Z] и = Х +X_T(t - τ).

Ущерб попытаемся оценить в данном случае коэффициентом:

u = К_τ = , (3.11)

учитывающем τ_А время актуальности задержанной информации (τ < τ_А).

При экспоненциальных зависимостях ценности информации от времени (актуальности) возможна формула:

u(τ) = exp(1 - ) (3.12)

Исходя из предположения о существовании некой усредненной вероятности р₀ успешной атаки на компонент (блок) Х с усредненным ущербом u₀, представляется возможным построение следующей стохастической модели для поражения (одним из вышеперечисленных видов атак) k блоков в множестве данных Х:

P(k) = p₀^k(1-p₀)^n-k (3.13)

или для нормированного элементарного риска:

_isk( )=( )p₀^k(1-p₀)^n-k=( ) p₀^k(1-p₀)^n-k

Интегральный риск может быть найден из суммы следующей прогрессии R_isk= p₀^k(1-p₀)^n-k. Соответственно интегральная защищенность данных в рассматриваемом конфликте будет равна:

З = 1 - R_isk= p₀^k(1-p₀)^n-k (3.14)

Предложенная формализация, очевидно, может быть углублена и расширена на иные ситуации информационной конфликтологии.

На основе предложенной модели осуществим оценку риска и ущерба социотехнической системы, подвергающуюся деструктивным изменениям ее параметров [119].

Пусть Х - множество входных и внутренних переменных состояния (данных) системы, Y - множество ее выходных переменных состояния. Пусть система описывается функцией F: X→Y. Поскольку данные подвергаются информационным операциям и атакам, то вместо хХ возможно использование данных  . Для оценки введем функцию ρ(y, ) при уY,  , которая показывает величину ущерба, понесенного из-за принятия решения вместо y. В качестве ρ можно использовать метрику в Y. Ущерб, вызванный искажением входных данных, есть ρ (F(x), F( )).

Пример: Рассмотрим мошенническую операцию, когда злоумышленник пытается реализовать несанкционированный перевод денег на свой счет. В этом случае обычно пытаются изменить оператор F (скажем, его адресную составляющую). Тогда ущерб будет равен разности остатков на счету до и после операции u= ρ[F(x), (x)]=Y- .

Возможно также изменение входных данных , ведущее к аналогичному результату.

Метрикой в некотором множестве Y называется функция ρ: Y  Y → R, такая, что при любых x,y,zY: a) ρ(x,y)≥0; б) ρ(x,y)=0, тогда и только тогда, когда x = y; в) ρ(x,y) = ρ(y,x); г) ρ(x,y) + ρ(y,z) ≥ ρ(х,z).

В классической теории дифференциальных уравнений с каждой точкой хХ можно связать область допустимых значений G(x), в которую входят все те , которые могут рассматриваться вместо х без существенного нарушения безопасности анализируемой системы. Тогда максимально допустимый ущерб есть точная верхняя грань: U[x, G(x)] = , число α называется точной верхней гранью некоторого числового множества Х( ), если: а) α не меньше любого хХ и б) для любого β < α существует по крайней мере одно х(β)Х, такое, что х(β) > β.

Пусть τ - метрика в Х и в качестве G(x) можно рассматривать шар { :τ(x, ) ≤ r} некоторого радиуса r безопасности с центром в х. Чем радиус шара r меньше, тем входные данные ближе к штатному их значению.

Представляется естественным изучить поведение модели при различных радиусах безопасности и особенно при r → 0. Несколько обобщая, будем считать, что с каждой точкой хХ связано семейство областей допустимых ущербов G_r(x), где r - произвольное положительное число. Наряду с максимально возможным ущербом U[x,G(x)], определенным выше, рассмотрим: U(x) = .

Если X и Y – совокупности действительных чисел, то ρ (y, ) = | y - |, τ(x, )=|x- |. В этом случае U(x)=0 тогда и только тогда, когда функция F непрерывна в точке x. Таким образом, понятие непрерывности есть частный случай обсуждаемого понятия безопасности[120].

Систему будем считать безопасной в точке х, если U(x)=0. Ее функция F называется ε – безопасной, если U(x)≤ ε в допуске ε (пороге безопасности).

Таким образом, имеются два основных элемента - функция F и область допустимых значений G. Простейшая задача - изучение опасности данной F при данной G в двух вариантах: при заданной G найти все безопасные F и, наоборот, по заданной F описать все G, при которых F является безопасной.

В стохастических моделях при реализации ИОА вместо детерминированных входных и промежуточных данных х приходится иметь дело со случайными величинами = (ω), приводящими у случайным потерям ρ[F(x), F( (ω))]. Чтобы характеризовать потери одним числом, рассматривают либо математическое ожидание М ущерба ρ, u_ср=Mρ[F(x), F( )], либо его квантиль u₀, определяемую из условия равенства вероятности P заданной величине α, P{ρ [F(x), F( )] ≤ u₀} = α.

Величины, задаваемые данными формулами, являются некоторыми аналогами ущерба. Очевидно, интерес представляют и другие оценки (моды, медианы и т.п.), однако принципиальную важность имеет такая характеристика, как риск Risk = UP, представляющий собой произведение величины ущерба U на вероятность P ее появления. Именно он характеризует шансы системы с точки зрения ее безопасности, поэтому фундаментальные исследования в данном направлении составляют особый научный интерес.

Кроме того, принципиально возможны три трактовки ущерба:

- параметрический, когда u = ρ[F(x),F( )];

- алгоритмический, когда u = ρ[F(x), (x)];

- гибридный, когда u = ρ[F(x), ( )].

Пример: При мошеннических операциях с банковскими картами задача злоумышленника сводится к введению верного кода клиента и нужной суммы, не вызывающих подозрений у банка. Т.е. вводятся верные исходные данные х. Успех злоумышленника в данном случае будет равен ущербу банка:

u=ρ[F(x), ] = Y (3.15)

Отклонения выходных данных, также как и входных, здесь отсутствуют = =, ибо эквивалентны запрошенной и полученной злоумышленником денежной сумме.