3. Контрольные вопросы
3.1. Какое уравнение называется линейным дифференциальным уравнением второго порядка?
3.2.
Сформулируйте теорему о дифференцировании
оригинала. Какие изображения будут
иметь первая и вторая (
и
)
производные оригинала?
Как перейти в дифференциальном уравнении от оригинала к изображению?
В чем состоит метод Крамера и метод Гаусса решения системы линейных алгебраических уравнений?
Назовите 4 типа элементарных рациональных дробей. В чем заключается метод неопределенных коэффициентов представления рациональной дроби в виде суммы элементарных дробей?
С помощью таблицы найдите оригинал, соответствующий изображению
.
4. Типичные задачи
4.1. Найти
решение уравнения
при начальных условиях
,
.
Найти решение уравнения
при начальных условиях
,
,
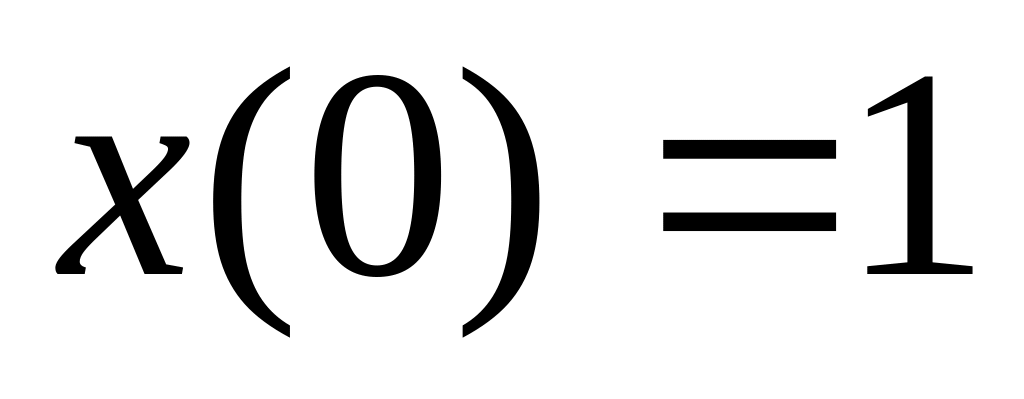.Найти решение системы дифференциальных уравнений
при
начальных условиях
5. Ответы к задачам
4.1. 
.
4.2.
4.3.
6. Примеры решения задач по теме занятия
1. Найти решение дифференциального
уравнения
,
удовлетворяющее начальным условиям
,
.
Решение. Пусть
.
По теореме о дифференцировании оригинала
и таблице изображений получим изображающее
уравнение
Подставляя начальные данные, имеем
Отсюда
находим
.
Разложим
дробь
на сумму простейших дробей
и
получим систему уравнений для определения
коэффициентов
и
Отсюда
находим
,
Таким образом, имеем
.
По таблице изображений находим решение
уравнения в пространстве оригиналов
2. Найти общее решение уравнения
.
Решение. По таблице изображений находим
.
Полагая , имеем
где числа
и
играют роль произвольных постоянных.
Изображающее уравнение имеет вид
.
Отсюда
.
Преобразуем первое слагаемое для
и найдем по таблице соответствующий
ему оригинал
Для второго слагаемого имеем
Для отыскания оригинала последнего слагаемого разложим его на простейшие дроби
.
Система уравнений для определения коэффициентов разложения имеет вид
Откуда находим
,
,
.
Следовательно,
Собирая оригиналы всех слагаемых, находим решение уравнения
.
Положим
,
,
получим
3.
Найти
решение уравнения
при начальных условиях
Решение.
Найдем прежде всего изображение правой
части. Так как
(формула 12), то по теореме затухания
.
Учитывая, что
и
составим операторное уравнение:
;
отсюда
.
Оригинал
для первого слагаемого находим по
формуле, указанной выше. Так как
,
то
(теорема смещения в изображении).
Второе слагаемое запишем в виде
.
Тогда
и окончательно
.
4. Найти решение системы дифференциальных уравнений
при
начальных условиях
Решение.
Если считать, что
и
,
то по теореме дифференцирования оригинала
и
(для
краткости записи мы не пишем аргументы
функций). Система операторных уравнений
примет вид
или, после преобразования,
В
результате мы получили систему
алгебраических линейных уравнений
относительно неизвестных изображений
и
Решая эту систему, находим
и,
возвращаясь к оригиналам,
5. Найти решение однородной системы
при начальных условиях
.
Решение. Система операторных уравнений запишется в виде
Эту систему решим при помощи определителей. Определитель системы равен
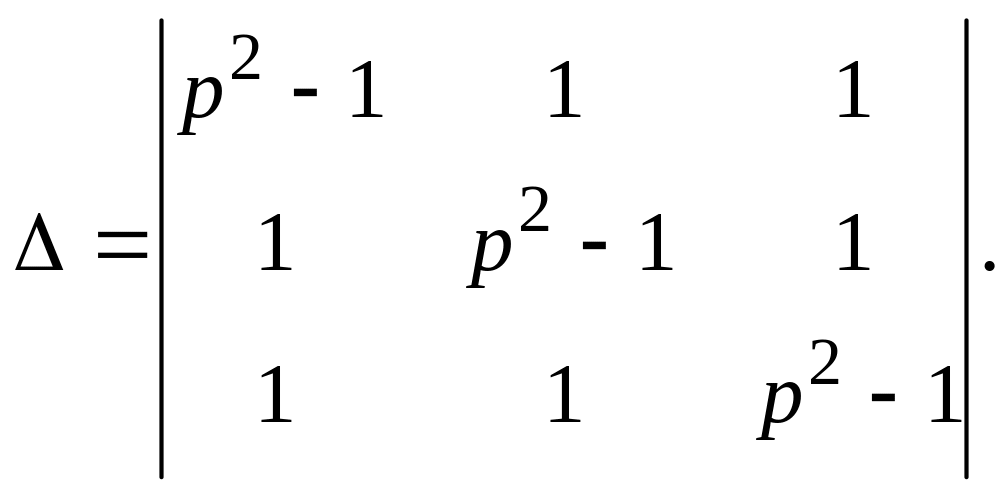
Вычислим его, опираясь на свойства определителей (сначала к первому столбцу прибавим оба остальных столбца, а затем из второй и третьей строк вычтем первую; в результате этих преобразований определитель не изменится):
=
.
Вычислим
определители
=
=
=
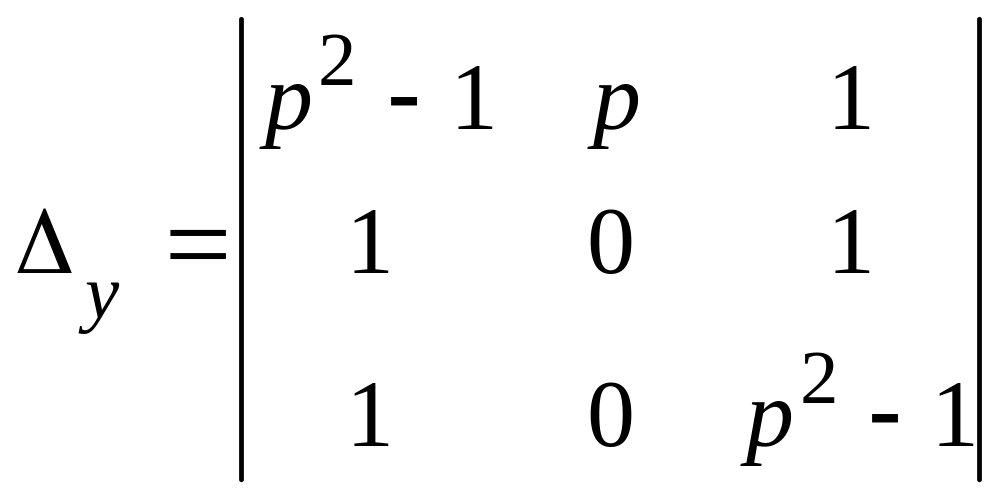Теперь находим изображения искомых решений:
Для перехода к оригиналам воспользуемся формулой, согласно которой:
Применяя
теорему дифференцирования оригинала,
находим
.
Снова
применяя эту же теорему, получим (каждый
раз значение оригинала при
равно нулю)
