3 Примеры заданий

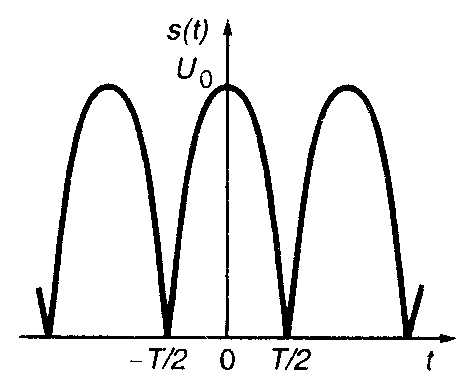
3.1. Периодический сигнал s(t) с периодом T на отрезке –T/2 ≤ t ≤ T/2 задан выражением s(t) = U₀cos(πt/T) (рис. 5.4). Найдите выражения для коэффициентов C_n ряда Фурье этого сигнала.

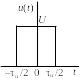
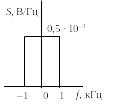
Рис. 5.4	Рис. 5.5	Рис. 5.6	Рис. 5.7

3.2. Найдите амплитуду A₂ второй гармоники сигнала, рассмотренного в задаче 3.1, если U₀ = 25 В.

3.3. Определите спектральную плотность униполярного прямоугольного импульса, изображенного на рис. 5.5. Постройте АЧХ и ФЧХ спектральной плотности при длительности импульса τ_и = 1 мс и амплитуде U = 1 В. Используя полученные графики, постройте аналогичные зависимости для импульсов вдвое меньшей длительности. Отобразите на графиках влияние задержки импульса на время τ_и/2.

3.4. Найдите спектральную плотность треугольного импульса, изображенного на рис. 5.6.

3.5. Найдите сигнал, соответствующий спектру S(ω), представленному на рис. 5.7. Аргумент спектральной плотности φ(ω) = 0 на всех частотах.

3.6. Периодический сигнал s(t), в общем случае комплексный, имеет заданный период T. Получите выражение, связывающее среднюю за период мощность этого сигнала P_ср с коэффициентами C_n его ряда Фурье.

4 Методические рекомендации и ответы

К заданию 3.1. Указание.

ω₁ = 2π/T, .

Воспользуйтесь тем, что .

Ответ: .

К заданию 3.2. Ответ. A₂ = 2,122 В.

К заданию 3.3. Указание и ответ.

Спектральная плотность прямоугольного импульса (5.8)

.

Зависимости АЧХ и ФЧХ спектральной плотности от частоты f при заданных длительности импульса 1 мс и амплитуде 1 В определяются по формулам

,

φ = –πn, n · 10³ ≤ f < (n + 1) · 10³, n = 0, 1, 2, … .

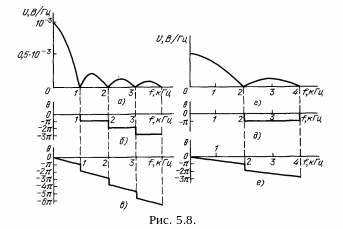
АЧХ показана на рис. 5.8а, а ФЧХ – на рис. 5.8б. При уменьшении длительности импульса в два раза, значения АЧХ и ФЧХ можно найти из тех же рисунков, изменив соответственно масштабы координат. На рис. 5.8г показана новая АЧХ, а на рис. 5.8д – новая ФЧХ. При сдвиге импульса на τ_и/2 АЧХ не изменяются, а ординаты ФЧХ уменьшаются на (ωτ_и/2. ФЧХ сдвинутых импульсов изображены при τ_и = 1 мс на рис. 5.8в и при τ_и = 0,5 мс – на рис. 5.8е.

К заданию 3.4. Ответ.

Спектральная плотность прямоугольного импульса (5.8).

К заданию 3.5. Ответ.

Рис. 5.9

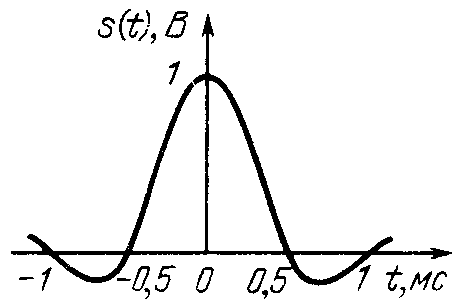
Раскрыв неопределенность при t = 0, получим s(0) = 1; s(t) обращается в нуль в точках , т.е. в моменты t_n = 0,5 · 10^–3n. Форма сигнала представлена на рис. 5.9 .

К заданию 3.6. Решение и ответ.

Средняя за период мощность комплекснозначного сигнала

.

, поэтому .

Вычисляя получаем, что для всех k≥1.

5 Домашнее задание

5

Рис. 5.10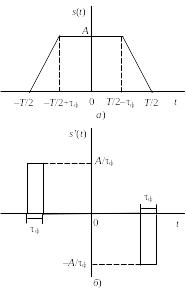

.1. Периодический комплексный сигнал s(t) с периодом T представлен следующими выражениями:

,

где A, α, τ – заданные вещественные числа.

Вычислите коэффициенты C_n ряда Фурье в комплексной форме для данного сигнала.

Ответ.

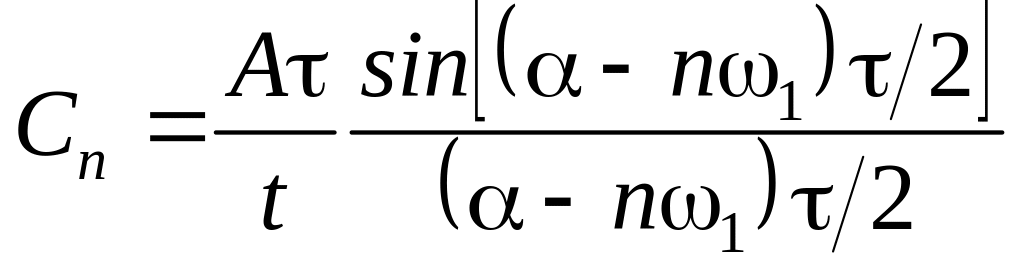
5.2. Найдите спектральную плотность трапецеидального импульса s(t), показанного на рис. 5.11а и его производной s’(t) (рис. 5.10б).

Указание и ответ. Сигнал s(t) определяется из сигнала s’(t) путем интегрирования. Представленный на рис. 5.11б сигнал является суммой двух прямоугольных импульсов. Пользуясь свойствами преобразования Фурье, можно определить спектральную плотность сигнала s’(t) – S(ω) и из нее получить спектральную плотность сигнала s(t) – S_c(ω), разделив S(ω) на jω. Определить S(ω) можно, пользуясь свойствами преобразования Фурье. Достаточно найти спектральную плотность одного импульса (рис. 5.11б) например, середина которого смещена влево на (T – τ_ф)/2 относительно начала координат:

.

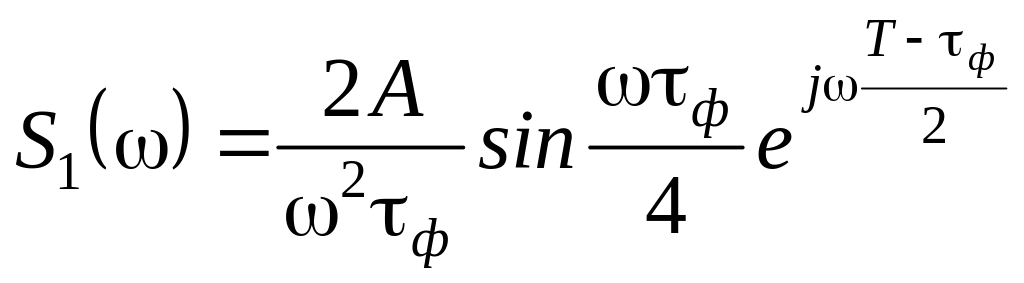Соответственно спектральная плотность второго импульса (по свойствам преобразования Фурье)

.

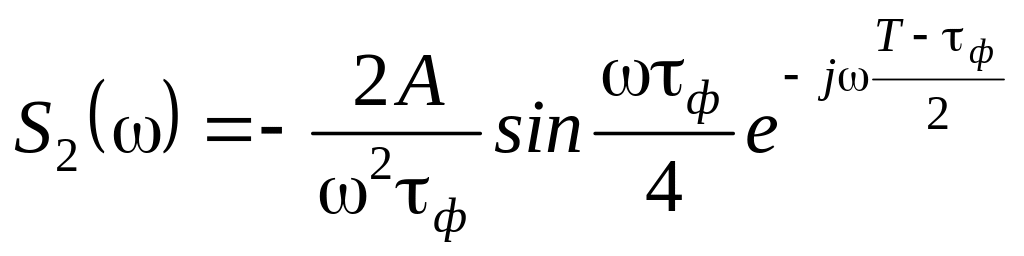Искомая спектральная плотность определяется как сумма спектральных плотностей обоих импульсов (еще одно свойство преобразования Фурье) и равна

.

Спектральная плотность сигнала s(t)

.

5.3. Найдите сигнал s(t), исходя из его спектральной плотности

.

Указание и ответ. На основании обратного преобразования Фурье получаем:

.

Здесь подинтегральная функция имеет два простых полюса, определяемых из уравнения 1 + ω²τ² = 0. Данные полюсы сосредоточены в точках с координатами .

Для вычисления сигнала s(t) при t < 0 следует провести интегрирование по контуру C₁ (рис. 5.11), включающему в себя бесконечно протяженную вещественную ось и дугу бесконечно большого радиуса, расположенную в верхней полуплоскости Imω > 0. Интеграл по указанной дуге стремится к нулю с ростом ее радиуса и поэтому

.

Вычет подинтегральной функции в точке полюсов res = e^–t/τ/(2jτ).

Итак,

/

А

Рис. 5.11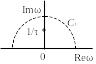

налогичный результат, отличающийся знаком в показателе экспоненты, будет получен для значений t < 0, при этом интегрирование следует проводить по контуру, замыкающемуся дугой бесконечно большого радиуса в нижней полуплоскости. Окончательно получим:

s(t) = S₀e^–|t|/τ/(2τ).

5.4. Определите энергии прямоугольного и треугольного импульсов (рис. 5.4, 5.5).