Тема №5 частные случаи систем двух случайных величин

Литература: [2], [3], [4].

Основные понятия

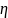Распределение двух случайных величин и , или

двумерной случайной величины (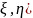 , не исчерпывается

распределением каждой из них , так как при этом не

учитывается зависимость, которая может существовать между ними.

Функции распределения 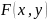двумерной случайной величины( , ) определяется как вероятность совместного выполнения неравенств < x и <y: .

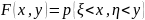Если представима в ви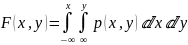де

, где 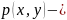некоторая

неотрицательная функция, то двумерную случайную величину

( , ) называет непрерывной, функцию плотностью

распределения двумерной случайной величины ( , ).

Плотность распределения 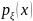случайной

величины выражается через совместную плотность p(x, y)

следующим образом:

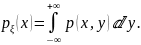
Аналогично для плотности распределения случайной

величины имеем 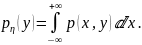В отличие от совместной плотности распределения p(x, y) одномерные плотности и 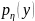называют маргинальными.

Случайные величины и называются независимыми,

если их совместная функция распределения при любых

значениях аргументов x, y равна произведению маргинальных

функций распределения 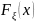случайной величины и

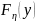
случайной величины :

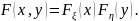
Пусть ( , 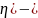непрерывная двумерная случайная

величина с плотностью распределения 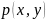. Тогда для

независимости и необходимо и достаточно, чтобы совместная плотность распадалась в произведение маргинальных плотностей и :

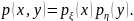
Коэффициент корреляции

Величина называется ковариацией

случайных величин 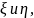cov ( , ). Если ( , непрерывная

двумерная случайная величина с плотностью распределения

, то

cov ( , )=

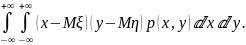
Величина r=cov( , )/ называется коэффициент

корреляции случайных величин .

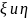Свойства коэффициента корреляции

1⁰. Модуль коэффициента корреляции не превосходит единицы,

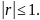
2⁰. Если независимые случайные величины, то r=0.

Обратное неверно: из условия r=0 (некоррелированность

случайных величин ) не следует независимость .

3⁰. Если связаны линейной зависимостью, то

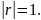
Свойства математического ожидания и дисперсии

1⁰. Математическое ожидание постоянной равно этой

постоянной, т.е.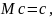

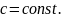
2⁰. Математическое ожидание суммы случайных величин

равно сумме их математических ожиданий, т. е.

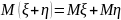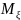(предполагается, что и 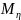существуют).

3⁰. Математическое ожидание произведения случайных величин равно произведению их математических ожиданий, т. е.

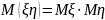(предполагается, что и существуют).

4⁰. Дисперсия постоянной равна нулю, т. е. ,

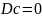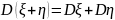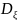5⁰. Дисперсия суммы случайных величин равно сумме их дисперсий, т. е. (предполагается, что и 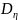существуют).

Пример решения задачи

Задача. Задана дискретная двухмерная случайная величина (X, Y);

X/Y	1	2	4
1	0.4	0.2	0.1
3	0.1	0.1	0.1

Найти: а) безусловные законы распределения составляющих; б) условный закон распределения Х при условии, что Y=3; в) условный закон распределения Y при условии, что Х=1; г) числовые характеристики двумерной случайной величины.

Решение. а) Сложим вероятности по столбцам и получим безусловный закон распределения Х:

X	1	2	4
P	0.5	0.3	0.2

Cложим вероятности по строкам. Безусловный закон распределения Y имеет вид:

Y	1	3
P	0.7	0.3

б) Вычислим:

p(x₁/y₂)=p(x₁,y₂)/p(y₂)=0.1/0.3=1/3,

p(x₂/y₂)=p(x₂,y₂)/p(y₂)=0.1/0.3=1/3,

p(x₃/y₂)=p(x₃,y₂)/p(y₂)=0.1/0.3=1/3.

Запишем искомый закон распределения Х:

X	1	2	4
P	1/3	1/3	1/3

в) Аналогично запишем закон распределения Y:

Y	1	3
P	4/5	1/5

г) Числовые характеристики вычислим по формулам:

M(X)= x₁P₁+x₂P₂+x₃P₃ =11/3+2 1/3+41/3=7/3,

здесь Р₁ ,Р₂ ,Р₃ необходимо брать из таблицы безусловного закона распределения Х, Р. Аналогично вычислим M(Y)= 14/5+31/5=7/5. Дисперсия D(X)=x₁² p₁+x₂² p₂ +x₃² p₃ – M ²(X)=1²1/3++2² 1/3+4²1/3 - (7/3)²=14/9 D(Y)=1²  4/5+3²  1/5- (7/5)²=16/25. Cредние квадратические отклонения

 (X)=  (14/9),  (Y)=(16/25)

Форма отчетности: устный опрос