Тема №6 вычисление доверительного интервала

Литература: [2], [3], [4].

Основные понятия

Кроме точечных оценок используются так называемые

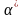
доверительные интервалы: указывается не одна точка 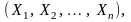а интервал 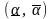, к которому с заданной

вероятностью принадлежит истинное значение параметра α,

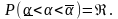
Число 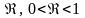называется доверительной вероятностью и характеризует надежность полученной оценки: чем ближе 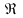к единице, тем надежнее оценка (обычно выбирают

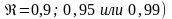. Величины α и 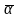называются доверительными границами. Они являются функциями выборочных значений 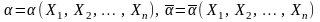и, следовательно, являются случайными величинами.

Интервал со случайными границами

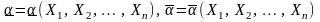, которые при любом допустимом значении α удовлетворяют соотношению для α , называется доверительным интервалом для неизвестного параметра α.

Примеры доверительных интервалов

1. Доверительный интервал для математического ожидания а нормальной случайной величины при известной дисперсии имеет вид

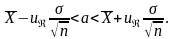
Здесь 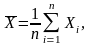величина определяется по заданной доверительной вероятности с помощью соответствующих таблиц, приведенных в приложениях . Доверительный интервал для математического ожидания а нормальной случайной величины при неизвестной дисперсии имеет вид

,

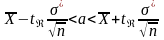где оценка 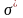вычисляется по формуле

,

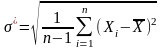а величина определяется по заданной доверительной

вероятности и объему выборки n с помощью соответствующих таблиц, приведенных в приложениях [3].

3. Доверительный интервал для дисперсии нормальной случайной величины имеет вид

,

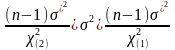где n – объем выборки; - оценка величины 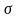, определяемая формулой ; 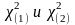- корни уравнений

,

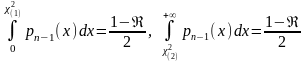в которых подынтегральная функция 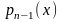представляет

собой плотность распределения хи-квадрат с n-1 степенями свободы. Уравнения при заданной доверительной вероятности решаются с помощью соответствующих таблиц, приведенных в приложениях . При определении 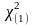входами служат 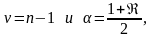при определении

.

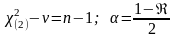4. Пусть n – число независимых испытаний, m – число

наступлений события A, p – вероятность наступления события

A в каждом отдельном испытании. Рассмотрим случай, когда

n достаточно велико, а значение p не слишком близко к нулю

или к единице так, что можно воспользоваться асимптотикой

Муавра-Лапласа . При этом доверительный интервал

для p имеет вид ,

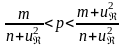определяется по заданной доверительной вероятности с помощью соответствующих таблиц, приведенных в приложениях [4].

Рассмотрим отдельно случай m=0. При этом нижняя доверительная граница равна нулю, верхняя 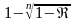. Аналогично, при m=n нижняя и верхняя доверительные границы равны соответственно 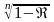и единице.

Форма отчетности: устный опрос, контрольная работа.

Тема №7 статистические оценки параметров распределения. Методы расчета сводных характеристик. Проверка статистических гипотез

Литература: [2], [3], [4].

Основные понятия

Случайная величина X, которая служит для статистической проверки гипотезы, называется критерием. Иногда термином критерий обозначают не только случайную величину X, но и все правило проверки в целом. При этом X называют статистикой критерия. Проверка гипотезы состоит в том, что если наблюдаемое значение критерия принадлежит некоторому определенному множеству S, т.е. наступает событие 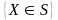, то основная гипотеза 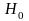отвергается.

Множество S, такое, что при наступлении события

основная гипотеза отвергается, называется критическим множеством (для гипотезы ).

Событие , состоящее в том, что основная гипотеза отвергается, когда она является истинной, называется ошибкой первого рода. Событие 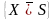, состоящее в том, что основная гипотеза не отвергается, когда верна одна из альтернативных гипотез 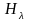, называется ошибкой второго рода. Вероятности ошибок первого и второго рода

вычисляются в предположениях о справедливости различных

гипотез – основной и альтернативной соответственно:

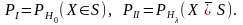Вероятность ошибки второго рода, а также вероятность 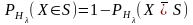противоположного события связаны с конкретной альтернативной гипотезой , т.е. могут зависеть от некоторого параметра λ. Функция для параметра λ, равная вероятности отвергнуть гипотезу , если верна гипотеза , называется

функцией мощности критерия. Правило статистической проверки гипотезы

1. Задаются малым числом α>0, называется уровнем значимости критерия; обычно α=0,05; 0,01 или 0,001. Чем более опасными признаются ошибки первого рода, тем меньшее

значение α должно быть выбрано.

2. Определяют критическое множество S из условия

выполнения неравенства

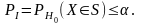
3. Условием критическое множество определяется

неоднозначно. Выбирают ту из возможностей, которая обеспечивает минимум вероятности ошибки второго рода, или, что то же самое, максимум мощности критерия.

4. Производят опыт и получают наблюдаемое значение критерия. Если при этом наступает событие 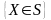, то основная гипотеза отвергается. В противном случае считается, что не противоречит опытным данным. Результат проверки гипотезы выражается словами: гипотеза отвергается (не отвергается) на уровне значимости α. Критерий согласия .

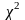Критерии, которые служат для проверки гипотезы о законе распределения случайной величины, называются критериями согласия. Пусть основная гипотеза состоит в том, что функция распределения случайной величины ξ есть вполне определенная функция F(x).Разобьем числовую ось на r промежутков (разрядов) (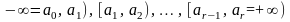 , где . При справедливой гипотезе i-му разряду 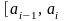соответствует вероятность 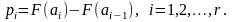Из n выборочных значений случайной величины ξ в i-й разряд 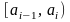попадает случайное число 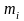значений . 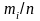Тогда отношение к вероятностям 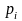свидетельствует в пользу основной гипотезы , заметные различия отвергают гипотезу . Случайная величина

Характеризует согласованность гипотезы с опытными данными. Критерий применяется в соответствии с общим правилом статистической проверки гипотез. При этом наблюдаемое значение критерия вычисляется по формуле , критическое множество выбирается в виде полу бесконечного интервала , где величина находится с помощью соответствующих таблиц, приведенных в приложениях(см. [4]). Входами таблицы служат величина 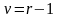и уровень значимости α. Если выполняется соотношение 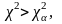то говорят, что гипотеза отвергается на уровне значимости α.

Замечание 1. Число выборочных значений в каждом разряде должно быть не менее 5-10. Если это условие не выполняется, рекомендуется объединить разряды.

Замечание 2. Критерий согласия применим не только в случае, когда гипотетическая функция распределения

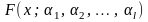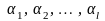F(x) случайной величины ξ полностью определена. Если она зависит от l неизвестных параметров, т.е. имеет вид , и параметры оцениваются по выборке методом максимального правдоподобия , то критерий согласия остается в силе, только входом служит величина .

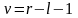Пример решения задачи

Используя критерий Пирсона, при уровне значимости 0,05 проверить, согласуется ли гипотеза о распределении генеральной совокупности Х по закону Пуассону с эмпирическим распределением выборки объема n =2 00.

xi	0	1	2	3	4
ni	116	56	22	4	2

Решение. Выборочная средняя x_в=( x_i n_i )/n=0.6. Предполагаемый закон Пуассона имеет вид: P_n(i)=(0.6)ⁱ exp(-0.6)/i!, т. е. P₀=P₂₀₀(0)=0.5488, P₁=P₂₀₀(1)=0.3293, P₂=P₂₀₀(2)=0.0988, P₃=P(3)=0.0198, P₄=P₂₀₀(4)=0.0030. Теоретические частоты m_i=nP_i=200P_i. Определим m₀=109.76, m₁=65.86, m₂=19.76, m₃=3.96, m₄=0.6. Малочисленные частоты m₃, m₄ можно объединить в новые n₃=4+2=6 и m₃=3.96+0.6=4.56.

Теоретическая частота ² = (n_i-m_i)² /m_i=2.54.

По таблице критических точек распределения (см. приложение таблица 4), по уровню значимости  =0.05 и числу степеней свободы k=s-2=2 находим критическую точку правосторонней критической области _кр² (0.05,2)=6.0. Так как ² < _кр², то имеется подтверждение гипотезы о распределение случайной величины X по закону Пуассону.

Форма отчетности: устный опрос, контрольная работа.