Тема №3 приложение теорем умножения и сложения вероятностей, формулы байеса.

Литература: [2], [3], [4].

Основные понятия

Теорема сложения и формула умножения вероятностей

Условной вероятностью события A при условии, что произошло событие В, называется число P(A/B), определяемое по формуле

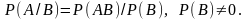
Из данного определения вытекает формула умножения

вероятностей

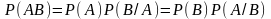
для двух событий, которая допускает следующее обобщение для n событий:

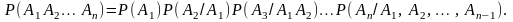
События А и В называются независимыми, если выполняется соотношение

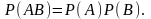
Теорема. Для любых событий А и В имеет место формула

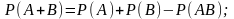
для n событий – формула

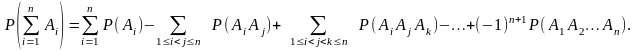
Условной вероятностью события A при условии, что произошло событие В, называется число P(A/B), определяемое по формуле

Из данного определения вытекает формула умножения

вероятностей

для двух событий, которая допускает следующее обобщение для n событий:

События А и В называются независимыми, если выполняется соотношение

Теорема. Для любых событий А и В имеет место формула

для n событий – формула

Формула полной вероятности, формулы Байеса

Набор событий называется полной группой попарно несовместных событий, если

H₁+H₂+…+H_n=Ω и H_iH_j=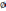 , I,j=1, 2, …, n, i=j,

где Ω достоверное событие; невозможное событие.

Теорема 1. Если H₁, H₂, …, H_n – полная группа попарно

несовместных событий, причем P(H₁) ≠ 0, i=1, 2, …, n, то для

любого события A имеет место равенство (формула полной

вероятности)

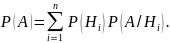
Теорема 2. В условиях теоремы 1 для любого события A, такого , что P(A) 0, справедливы формулы Байеса

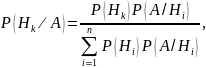k = 1, 2, …,

Пример решения задачи

Задача. В первой урне содержится 12 шаров из них 8 белых; во второй урне 20 шаров, из них 6 белых. Из каждой урны наудачу извлекли по одному шару, а затем из этих двух шаров взят один шар. Найти вероятность того, что взят белый шар.

Решение. Пусть вероятность P(А) – искомая вероятность. Событие H₁ - выбор из 1- ой урны и из 2- ой по белому шару, H₂ - выбор из 1-ой урны и из 2-ой по черному шару, а H₃ - выбор из 1-ой урны белого шара и из 2-ой урны черного шара или выбор из 1-ой урны черного шара и из 2-ой урны белого шара. Beроятности: Р( H₁ )=(8/12)(6/20)=48/240,

P(H₂)=(4/12)(14/20)=56/240,P(H₃)=(8/12)(14/20)+(4/12)(6/20)=136/240.

Условные вероятности:

P( A/H₁ )=1, P( A/H₂ )=0, P(A/H₃)=0.5. Вероятность P(A)=

P(H₁)P(A/H₁)+P(H₂)P(A/H₂)+P(H₃)P(A/H₃)= =(48/240)1+(56/240)0+ (136/240)0.5=29/60.

Форма отчетности: устный опрос, контрольная работа.

Тема №4 числовые характеристики биноминального, равномерного, показательного и нормального распределений, распределения пуассона

Литература: [2], [3], [4].

Основные понятия

Случайной величиной 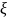называется функция 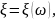определенная на пространстве элементарных событий

Это определение является точным в случае дискретного

пространства элементарных событий Ω. В общем случае на

функцию 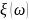накладывается требование измеримости.

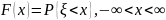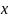Функцией распределения случайной величины называется функция .Иными словами, значение функции распределения – случайной величины – есть вероятность того, что принимает значение меньшее, чем .Случайная величина называется дискретной, если

существует конечное или счетное множество чисел

x₁, x₂, …, x_k, … (без предельных точек), таких, что

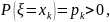k=1, 2, …;

Совокупность значений x_k и соответствующих

вероятностей 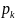называется распределением дискретной

случайной величины.

Примеры дискретных распределений

1. Биномиальное распределение

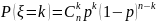, 0<p<1, k=0, 1, 2, …, n.

2. Распределение Пуассона

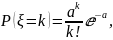a>0, k=0, 1, 2, …

3. Геометрическое распределение

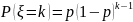, 0<p<1, k=1, 2, …

4. Гипергеометрическое распределение

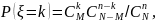k=0, 1, 2, …, min(M, n).

Случайная величина называется непрерывной

случайной, если ее функция распределения представима

в виде

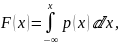
где 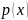– некоторая неотрицательная функция.

Подынтегральная функция в формуле называется

плотностью распределения случайной величины ,

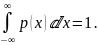
Примеры непрерывных распределений

1. Равномерное распределение

, .

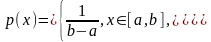
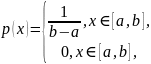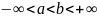2. Нормальное распределение (с параметрами (a, ))

, .

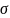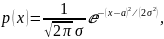
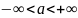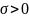3. Показательное распределение

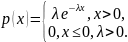
4. Распределение Коши

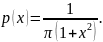
Можно сделать вывод, что в любой точке

непрерывности 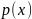имеет место равенство .

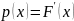Математическим ожиданием дискретной случайной величины

называется число

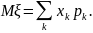
Если случайная величина принимает счетное множество значений, то требуется абсолютная сходимость ряда . Если ряд не сходится абсолютно, то говорят, что случайная величина не имеет математического ожидания.

Математическим ожиданием непрерывной случайной

величины число называется

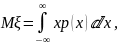
если интеграл абсолютно сходится.

Дисперсией D случайной величины называют

математическое ожидание случайной величины (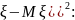

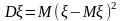. Для дискретной случайной величины дисперсия вычисляется по формуле

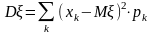
для непрерывной 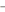по формуле

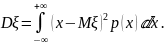
Вероятность того, что случайная величина

принимает значение в заданном числовом промежутке,

вычисляется по одной из формул:

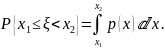
Форма отчетности: устный опрос..